Metod 1

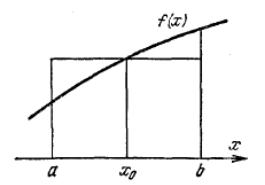
Полученная формула называется формулой Симпсона (формула парабол). Геометрически эта формула получается заменой данной кривой y f x

параболой y L2 x . Аналогично формуле трапеций, но, дифференцируя три раза, можно получить остаточный член формулы Симпсона:

R h

h5

f 4 , a,b .

90

Рассмотрим

общую

формулу

Симпсона.

Пусть

n 2m

и

xi a ih,

yi f xi , i 0,1,...,n,

h

b a

. Применяя формулу Симпсона к

n

каждому из промежутков

x0,x2

,...,

x

2m 2,x2m длины 2h, получим

b

h

h

f x dx

y0

4y1 y2 ...

y2m 2

4y2m 1 y2m

a

3

3

h

y0 yn 4 1 2 2 ,

3

где

1

y1

y3 ... y2m 1, 2

y2 y4 ... y2m 2 .

Остаточный

член

полученной формулы имеет вид:

n

h

5

m

4

5

m

f 4 i

5

m

4

i 1

i

h

i 1

h

,

R

f

f

90

90

m

90

где a,b .

y0 f x0 ,

где x0 a,b

Формула

прямоугольников.

Пусть

n 0 и

b

произвольная точка. Тогда L1 x y0 и f x dx b a y0 . При применении

						a
формулы прямоугольников мы заменяем
площадь				криволинейной		трапеции
площадью прямоугольника (рис. 1.2).
	Если			x0 a,	то	полученная
приближенная формула						называется
формулой левых прямоугольников, если
x0 b,		то она носит название формулы
правых			прямоугольников,			а, если
x	a b		,	то средних прямоугольников.			Рис. 1.2
0	2
		f C2 a,b ,
Пусть					тогда	остаточный

член данной формулы можно представить в виде:

11

b

b

R f x dx b a f x0 f x0 f x0 x x0

a

a

f

x x 2 dx b a

f x

2

0

0

f x0 b x0

2

a

x0

2

b

f

x x0 2 dx

a

2

2

b a

Пусть x

,

тогда первое слагаемое равно нулю.

Следовательно, если

0

2

f x

M , для всех x a,b , то получим

b x x0

2

M

3

R

M

dx

b a .

2

24

a

Рассмотрим

общую

формулу

прямоугольников.

Пусть

xi

a ih,

yi f xi

, i 0,1,...,n,

h

b a

. Применяя к каждому из отрезков

n

формулу прямоугольников, получим

x

0,x1 ,...,

xn 1,xn

b

n 1

x

i

x

i 1

n 1

x

i

x

i 1

f x dx xi 1 xi f

h f

.

2

2

a

i 0

i 0

Для остаточного члена получим следующую оценку:

										M			n 1									M nh	3
							R						i 0 xi 1 xi 3												.
										24												24									3
																																	1
	Пример 1.2. Вычислить с помощью формулы трапеций интеграл cos2																																	dx.
																														2			x
	Оценить погрешность.
	Решение. Имеем
		3
					1				3					2			1		2					2					1
		cos		2
						dx												cos				cos								.
					x														2					3					8
	2																2

Для оценки погрешности оценим вторую производную подынтегральной функции.

f x cos2							1
								x
					1						2
f		x x2						sin x
				2						2				2		2
f			x x3 sin x									x4			cos x

12

Следовательно,
	f x			2		2	2			3			4		22.
				3		4				3			4
				x		x			2		2

Поэтому							3 22
	R		3			2
									0,06.
								12

1.3. Метод Рунге практической оценки погрешности

Рассмотрим метод повышения порядка точности квадратурной формулы. Этот метод называется методом Рунге или методом двойного

b

пересчета. Пусть J f x dx - точное значение интеграла, а Jh -

a

приближенное значение интеграла, соответствующее шагу h разбиения отрезка a,b . Пусть Rh J Jh ph p qhq ..., p, q 0, p q остаточный член квадратурной формулы. Проведем расчеты на двух равномерных сетках с шагами h1 и h2 , и потребуем, чтобы погрешность их

линейной комбинации

R Rh1 1 Rh 2 Jh1 1 Jh2 J

была величиной более высокого порядка по сравнению с Rh1 и Rh2 . Имеем

R ph1p qh1q ... 1 ph2p qhq2 ...

p h1p 1 h2p q h1q 1 hq2 ...

Потребуем,

чтобы

h1p 1 h2p 0.

Отсюда

h2p

. Тогда

hp hp

R O hq , h max h1,h2 и J Jh1

2

1

1 Jh 2 R.

Пусть

теперь h1

h, h2 h/2.

Тогда

J Jh/2

Jh/2

Jh

O hq .

На

p

2

1

практике полученная формула заменяется приближенной:

J Jh/2

Jh/2 Jh

,

где p 2 для метода

2p 1

p 1

средних прямоугольников и трапеций,

для

методов левых и правых прямоугольников и p 4 для метода Симпсона.

13

1.4. Выполнение лабораторной работы по численному интегрированию в среде MathCad

Целью данной работы является ознакомление студента с основными методами численного интегрирования, выработка навыков решения простейших задач, знакомство с основными функциями среды MathCad.

Разберем порядок выполнения данной работы. Работа состоит из двух заданий. В первом задании требуется найти приближенное значение интеграла с заданным шагом сетки h одним из предлагаемых студенту методов. Требуется так же оценить погрешность. Это задание выполняется студентом вручную дома. Второе задание – это нахождение приближенного значения интеграла с заданной точностью . Задание выполняется в компьютерном классе с использованием среды MathCad. Рассмотрим пример. Пусть дан интеграл

3

cos2 1xdx.

1

Требуется найти его приближенное значение по формуле средних прямоугольников с шагом h 0.2 и оценить погрешность по методу Рунге.

Решение. Имеем

	3	2	1		9	2		1
	I cos			dx I	0,2 0,2 cos					1,433.
			x					1,1 i 0,2
	1				i 0

Для оценки погрешности найдем приближенное значение интеграла с шагом h 0,4:

	4							2				1
I	0,4 0,4 cos														1,438
										1,2 i 0,4
		i 0
Следовательно,						I	0,2 I0,4
		I I0,2											0,0017.
										3

Второе задание лабораторной работы состоит в нахождении приближенного значения интеграла с заданной точностью. Соответствующий этому заданию документ MathCad приведен в листинге 1.1.

14

Листинг 1.1. Численное интегрирование

15

ГЛАВА 2. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ОБЫКНОВЕННОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ

Задача Коши для обыкновенного дифференциального уравнения

первого порядка состоит в отыскании решения y(x) уравнения
			dy	f x,y ,		(2.1)
			dx
удовлетворяющего начальному условию
			y x0 y0			(2.2)
Разобьем отрезок	x0;X , на котором ищем решение, на					n равных
интервалов с шагом	h	X x0			. Получим следующие точки	деления:
		n

x0, x1 x0 h,...,xn x0 nh X . Точки xk называются узлами разностной сетки, расстояние h между узлами – шагом разностной сетки, а совокупность заданных в узлах сетки значений какой-либо величины называется сеточной функцией {yk , k 0,1,...,n}. Приближенное решение задачи Коши будем искать численно в виде сеточной функции.

При решении задачи Коши численным методом для любого xi

определим приближенно yi y xi , i 1,2,...,n. Величина погрешности этих

значений, т.е. разность между точным решением и приближенным в соответствующих точках, определяет погрешность метода. В данной главе мы рассмотрим различные методы численного решения задачи Коши.

2.1. Метод Эйлера

Пусть известно значение y x и требуется вычислить значение y x h . Рассмотрим равенство:

h
y x h y x y x t dt.	(2.3)
0

Как было показано в главе 1, при замене интеграла в правой части на h y x

погрешность имеет порядок O h2 . Таким образом,

y x h y x y x h O h2 .

Поскольку y x f x,y x , то мы получаем

y x h y x h f x,y x O h2 .

Отбрасывая член порядка O h2 , и обозначая xj x, xj 1 x h, получаем формулу Эйлера:

y j 1 yj h f xj,yj .

16

2.2. Различные модификации метода Эйлера

Для получения более точной формулы нужно точнее аппроксимировать интеграл в правой части.

Воспользуемся квадратурной формулой трапеции, получим y x h y x h2 y x y x h O h3 ,

или иначе,

y x h y x h2 f x,y x f x h,y x h O h3 .

Заменим y x h в правой части полученной формулы на некоторую величину y* y x h O h2 . Тогда правая часть изменится на величину

h2 f x h,y* f x h,y x h h2 fy x h,y y* y x h O h3

( y находится между y* и y x h ). Таким образом, имеет место соотношение

y x h y x h2 f x,y x f x h,y* O h3 .

Условию y* y x h O h2 удовлетворяет результат вычислений по формуле Эйлера y* y x hf x,y x . Эти соотношения определяют пару расчетных формул:

	y*j 1 yj	hf xj,yj ,
			h	(2.4)
	yj 1 yj			f xj,yj f xj 1,y*j 1 .
			2

Рассмотренный метод носит название метода Эйлера-Коши.

Построим другую пару формул с погрешностью на шаге того же порядка. Интеграл в правой части (2.3) заменим по формуле средних прямоугольников:

				h		O h				3	,
y x h y x hy x
				2
или
	h						h		O h			3	.
y x h y x hf x			,y x
	2					2

	*		h		O h	2	, то, как и в предыдущем случае, имеем
Если y		y x
			2

y x h y x hf x h,y* O h3 .

2

17

В качестве y* можно взять результат вычислений по формуле Эйлера с шагом h2: y* y x h2 f x,y x . Этим соотношениям соответствует пара расчетных формул, определяющих еще одну модификацию метода Эйлера:

y

1 yj

h

f xj,yj ,

j

2

2

(2.5)

h

yj 1 yj

h f xj

,y

1 .

2

j

2

2.3. Оценка погрешности по правилу Рунге

Пусть yi1 ,xi :i 0,1,...,n

и y j2 ,xj :i 0,1,...,2n

решения задачи

Коши, полученные с шагами h

X x0

и

h

. Тогда в совпадающих узлах,

n

2

имеет место, приближенное равенство:

y 1

y 2

y x2i y22i

i

2i

,

2

s

1

где s 1 для метода Эйлера и s 2 для рассмотренных его модификаций.

На практике применяют следующий метод: выбрав из каких-либо

соображений шаг интегрирования h, проводят вычисления с шагом h и

h

y 1 y 2

2

и сравнивают результаты. Если

в общих

точках

,

где

-

2s 1

заданная точность, то считают,

что шаг h

2

удовлетворяет

заданной

точности. В противном случае проводят вычисления с шагами h и h и т.д.

2 4

Пример 2.1. Методом Эйлера с точностью 0,06 решить задачу Коши y x y,

y 0 1

на отрезке 0;0,4 .

Решение. Вычисление происходит по схеме:

yj 1 yj h f xj,yj .

Оценка погрешности происходит по правилу Рунге:

	y 1 y 2			,	s 2.
	2s 1	1

Положим h 0,4. Тогда, по методу Эйлера, получим следующую сеточную функцию, являющуюся приближенным решением данного уравнения

18

x0 0; y00,4 1;

x1 0,4; y10,4 1 0,4 0 1 1,4.

Положим h 0,2. Получим следующую сеточную функцию:

x0 0; y00,2 1;

x1 0,2; y10,2 1 0,2 0 1 1,2;

x2 0,4; y20,2 1,2 0,2 0,2 1,2 1,48.

Оценим погрешность в совпадающих точках.

y20,2 y10,4 0,08 0,06.

Положим h 0,1, получим

x0 0; y00,1 1;

x1 0,1; y10,1 1 0,1 0 1 1,1;

x2 0,2; y20,1 1,1 0,1 0,1 1,1 1,22;

x2 0,3; y30,1 1,22 0,1 0,2 1,22 1,362; x2 0,4; y40,1 1,362 0,1 0,3 1,362 1,5282.

Оценим погрешность в совпадающих точках. y10,2 y20,1 0,02 0,06;

y20,2 y40,1 0,0482 0,06.

Таким образом, решением, удовлетворяющим заданной точности, будет то, которое получено с шагом h 0,1.

2.4. Методы интегрирования систем дифференциальных уравнений и уравнений n- го порядка

Интегрирование дифференциального уравнения n-го порядка сводится к интегрированию системы дифференциальных уравнений. Действительно, пусть дано дифференциальное уравнение n-го порядка:

yn f x,y,y ,...,y n 1 .

Будем считать в этом уравнении неизвестными не только y, но и y y1 , y y2 , …, y n 1 yn 1, тогда данное уравнение заменяется системой

19

y y1,

y1 y2,

............

		yn 1,
yn 2
		f x,y,y1,...,yn 1 .
yn 1
Поэтому мы рассмотрим		только методы интегрирования систем

дифференциальных уравнений.

Все изложенные методы приближенного интегрирования дифференциальных уравнений первого порядка без существенных изменений переносятся на системы уравнений первого порядка.

Пусть дана система дифференциальных уравнений первого порядка:

	dy1			f		x,y ,y ,...,y			,
dx					1		1 2	n
dy2				f	2 x,y1,y2,...,yn ,
										(2.6)
dx
.........................................
dyn				f	n x,y1,y2,...,yn ,
dx
и начальное условие
	yi x0 yi0,						i 1,2,3,...,n.			(2.7)

Систему (2.6) и условие (2.7) можно переписать в векторной форме. Для

этого введем векторы Y y1,...,yn и

F f1,..., fn . Тогда система (2.6) и

условие (2.7) перепишутся в виде:

dY

F x,Y ,

Y x0 Y0 .

(2.8)

dx

Напишем,

например,

метод Эйлера для

задачи

Коши (2.8). Пусть

x

x

jh, j 0,1,...

разбиение отрезка

x

, X

,

на котором ищется

j

0

0

решение задачи (2.8). Тогда вычисление будем производить по формуле

Yj 1 Yj hF xj,Yj .

Напишем теперь метод Рунге-Кутты четвертого порядка. Вычисления производятся по формуле:

	K j1 hF xj,Yj ,
				h					K j1
	K j2 hF xj					,Yj						,
			2						2
			h						K j2
	K j3 hF xj					,Yj						,
			2						2

20