Графический метод решения

Найдем множество решений системы неравенств. Рассмотрим 1-ое неравенство и заменим его точным равенством 7х₁ + 8х₂ = 474. Это уравнение прямой в плоскости х₁ох₂. Строим ее по двум точкам: х₁ = 0, и х₂ = 0, . Так как точка О(0; 0) удовлетворяет первому неравенству 7х₁ + 8х₂ ≤ 474 (7 · 0 + 8 · 0 ≤ 474), то и все точки полуплоскости, на которые прямая 7х₁ + 8х₂ = 474 делит плоскость х₁ох₂ и которая содержит точку О(0; 0) будут так же удовлетворять первому неравенству. Аналогично находим решение всех остальных неравенств и пересечение всех полуплоскостей, определяющих множество решений системы ограничений. Это будет выпуклое множество - многоугольник ОАВСД.

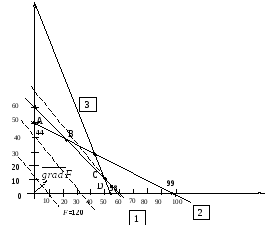
Придадим целевой функции произвольное значение, например F = 120 и построим соответствующую прямую 12x₁ + 10x₂ = 120. Найдем также координаты вектора , так как а , то gradF = {12, 10}.

Строим этот вектор. Известно, что в направлении вектора gradF функция F возрастает, а в противоположном направлении убывает. Поэтому, перемещая прямую в направлении grаdF, мы будем переходить от меньших значений F к большим. Тогда наиболее удаленная от начала координат в направлении grаdF точка области ОАВСД определит наибольшее значение функции F. Такой точкой будет точка С. Найдем ее координаты, решая совместно уравнения прямых 1 и 3.

,

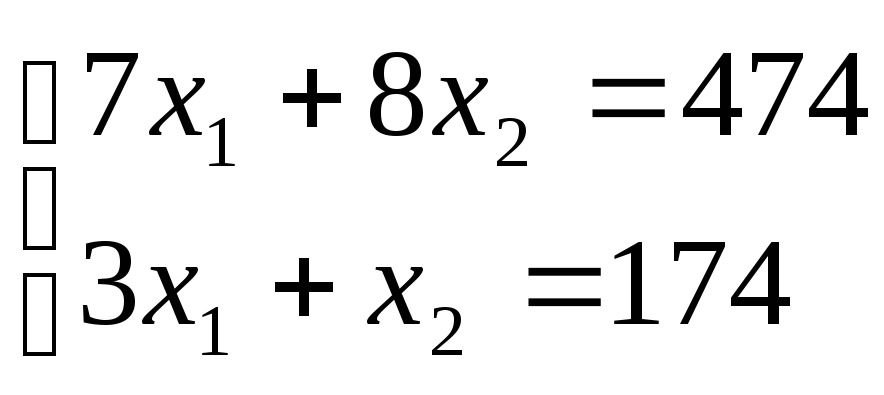
х₁ = 54, х₂ = 12.

Итак, Fmax = F(C) = F(54; 12) = 12· 54 + 10 · 12 = 768.

Таким образом, проведено графическое решение конкретной задачи линейного программирования. Машин вида А₁ нужно 54, вида А₂ – 12, при этом максимальная прибыль от их эксплуатации будет 768 ед. Такое решение возможно, если число неизвестных не больше двух. Если число неизвестных больше двух, то графическое решение невозможно. Проведем аналитическое решение этой же задачи. Соответствующий метод называется симплекс-методом и основан на применении метода Жордана – Гаусса решения систем линейных уравнений.

Симплекс-метод

Вернемся к математической модели рассмотренной выше задачи (4):

при

Перейдем от этой системы ограничений в виде неравенств к системе ограничений заданной уравнениями с помощью введения новых неизвестных х₃, х₄, х₅:

(6)

Экономический смысл новых неизвестных в том, что они определяют количество неиспользованных строительных материалов каждого вида. Очевидно, что система ограничений (4) эквивалентна системе (6). Перепишем последнюю систему в виде

(7)

Эта система уже приведена к единичному базису. Базисными неизвестными являются х₃, х₄, х₅, свободными – х₁ и х₂. Если свободным неизвестным придать нулевые значения, то получим значения базисных неизвестных: .

Решение такого вида, где свободные неизвестные равны нулю, называется базисным:

х₁ = 0; х₂ = 0; х₃ = 474; х₄ = 396; х₅ = 174. (8)

Если в базисном решении нет отрицательных значений неизвестных, то оно называется опорным (как в данном случае).

Значение целевой функции (5) при опорном решении (8) будет

.

Очевидно, что это решение не является оптимальным, так как увеличивая х₁ и х₂ мы будем получать большие значения F. Начнем увеличивать х_1, сохраняя за х₂ нулевое значение. Ясно, чем больше будет х₁, тем больше получим значение F. В то же время увеличение х₁ не должно привести к появлению отрицательных значений других неизвестных. Из 1-го уравнения системы (6) видно, что х₁, нельзя брать больше чем , второе уравнение не позволяет увеличить х₁ больше, чем , а третье - . Наименьшее из этих чисел .

Поэтому больше чем 58, х₁ брать нельзя, так как х₃ и х₄ примут тогда отрицательные значения. Пусть х₁ =58, а х₂=0. Тогда х₅ получит значение 0. Это значит, что за свободные неизвестные можно взять х₂ и х₅ , а базисными будут х₃, х₄ и х₁. Тем самым базисная неизвестная х₅ перешла в свободные, а неизвестная х₁ из свободных - в базисные.

Преобразуем систему (7) к новому базису, определяя х₁ из третьего уравнения этой системы.

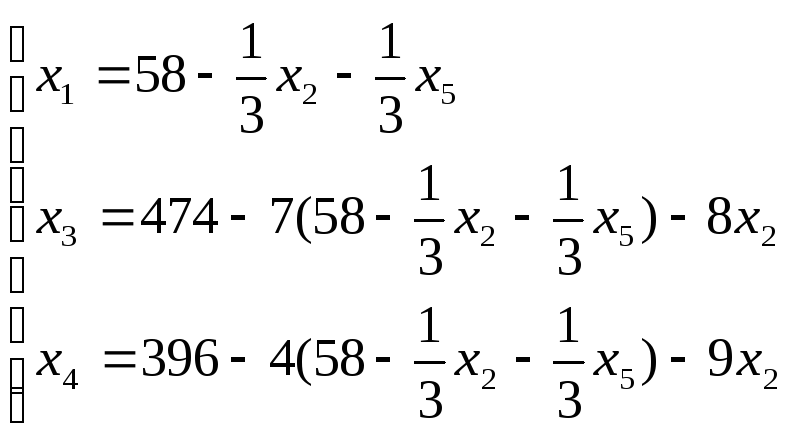
(9)

Новое базисное решение будет опорным. Целевую функцию F выразим так же через свободные неизвестные х₂ и х₅.

. (10)

При х₂ = 0 и х₅ = 0, получим F = 696. Это больше первоначального значения, но в то же время не оптимально, так как, увеличивая х₂ (сохраняя за х₅ нулевое значение) будем получать для F большие значения. Из системы (9) видим, что х₂ нельзя взять больше, чем , что соответствует второму уравнению.

Придавая х₂ значение 12 (оставляя х₅=0), получим х₃=0. Это значит, что за свободные неизвестные теперь можно взять х₃ и х₅, а за базисные х₁, х₂, х₃.Выразим х₂ из второго уравнения системы (9) и подставим это значение в остальные уравнения этой системы и в функцию F. Получим

; (11)

Базисное решение является опорным. При этом ( и это значение будет оптимальным (наибольшим), т.к. теперь уже увеличения будут только уменьшать F. Мы получили оптимальное решение Это значит, что машин вида А₁ должно быть 54, вида А₂ – 12, строительные материалы вида В₁ и В₅ будут использованы полностью, а материалов вида В₂ будет не израсходовано 72 ед., что совпадает с ранее найденным результатом.

Таким образом, процедура симплекс-метода состоит в переходе от одного опорного решения к другому.

Справедлива теорема: если оптимальное решение общей задачи линейного программирования существует, то оно достигается при каком- то опорном решении.

Коэффициенты перед свободными неизвестными в целевой функции F называются оценками этих неизвестных. Из проведенного алгоритма следует, что если задача формируется на максимум, то оптимальное значение F получается, если все оценки свободных неизвестных в целевой функции отрицательны (или равны нулю), т.е. неположительны. Это критерий максимума целевой функции F. Критерий минимума в том, что все оценки свободных неизвестных в целевой функции неотрицательны. Действительно, в таком случае целевую функцию уменьшить по сравнению со значением при нулевых свободных неизвестных, уже нельзя.

Проведенное решение лучше осуществлять в специальных симплекс-таблицах. Покажем это, исходя из системы (7).

В первую симплекс-таблицу фактически заносим систему (7) и целевую функцию F в виде: .

Базис	­ неизвестные					Свобод. члены
	х1	х2	х3	х4	х5	bi
х3	7	8	1	0	0	474
х4	4	9	0	1	0	396
¬х5	3	1	0	0	1	174
-F	12	10	0	0	0	0

Эта таблица соответствует системе (7).

Базисное (опорное) решение не оптимально, так как все оценки свободных неизвестных положительны. Перейдем к другому опорному решению, применяя метод Жордана – Гаусса. Разрешающий столбец выберем сами (это может быть первый или второй). Выберем первый. Разрешающую строку определим по

Таким образом, разрешающей строкой будет третья. На пересечении разрешающих строки и столбца находится коэффициент 3, который будет разрешающим. Поэтому, третью строку делим на 3, а затем умножая ее на (–7), на (–4), на (–12), прибавим к 1-ой, 2-ой, 4-ой строкам соответственно, получим новую симплекс-таблицу, в которой неизвестная х₁ из свободных перейдет в базисные, а х₅ – из базисных в свободные (это показано стрелками).

Базис	­ неизвестные					Свобод. члены
	х1	х2	х3	х4	х5	bi
¬х3	0		1	0		68
х4	0		0	1		164
х1	1		0	0		58
-F	0	6	0	0	-4	-696

Эта таблица соответствует системе (9) и целевой функции (10).

Базисное решение является опорным, но не оптимальным, т.к. в последней строке есть положительная оценка во втором столбце. Возьмем его за разрешающий. Разрешающую строку выберем из условия

, что соответствует первой строке.

Поэтому разрешающей строкой будет первая, а разрешающим элементом . Разделим первую строку на , а затем, умножая ее на , прибавим ко 2-ой, к 3-й, к 4-ой строкам соответственно. Получим новую симплекс-таблицу, в которой неизвестная х₃ из базисной перейдет в свободную, а х₂ – из свободной в базисную. Получим

Базис	Неизвестные					Свобод. члены
	х1	х2	х3	х4	х5	bi
х2	0	1		0		12
х4	0	0		1		72
х1	1	0		0		54
-F	0	0		0		-768

Эта таблица соответствует системе ограничений и функции F в виде (11).

Базисное решение является оптимальным, т. к. в последней строке нет положительных оценок. Последняя строка переписывается так:

.

Очевидно, что максимум F будет при и равен 768 ед.

Замечание. Если бы в последней симплекс-таблице, в последней строке была бы только одна положительная оценка, а в соответствующем столбце не было бы положительных чисел, то задача не имела бы решений, т.е. целевая функция не ограничена в области решений системы ограничений.

Геометрический смысл перехода от одного опорного решения к другому, т.е. переход то одной симплекс-таблицы к другой, состоит в том, что мы передвигаемся по многоугольнику ОАВСД от точки О к точке Д, а от нее к точке С.