11.2 Формула Стокса.

Формула Стокса устанавливает связь между КРИ и ПВИ.

Теорема 11.2. Если функции P(x,y,z), Q(x,y,z), R(x,y,z) непрерывны вместе со своими ЧП-1 в точках ориентированной плоскости S, то имеет место формула:

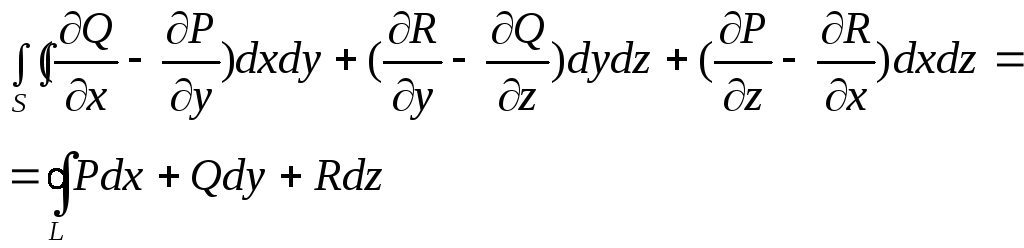(7)

L-гладкая замкнутая линия, граница которой поверхность S и интегрирование вдоль  прямой ведется в “+” направлении.

Замечание:

1. Формула Стокса выражает КРИ по замкнутому контуру через интеграл по поверхности натянутой на этот контур по этому применяется формула Стокса тогда, когда удобно заменить вычисление КРИ вычислением поверхностного интеграла.

2. Частным случаем формулы Стокса, когда L-гладкая замкнутая кривая на плоскости xOy, а поверхность S-часть плоскости xOy, ограниченной этим контуром L является формула Грина:

3. Из формулы Стокса следует, что при выполнении условий:

Из формулы Стокса следует, что КРИ по замкнутому контуру

при выполнений условия (3), а это означает, что КРИ не зависит от форму пути интегрирования.

11.3. Применение пви к вычислению объёмов тел.

Вычислим V тела, ограниченного сверху гладкой поверхностью образующей параллельной оси Oz.

Запишем формулу Остраградского-Гаусса:

Пусть:

1. P=x,Q=0,R=0  (8)

б) P=0,Q=y,R=0  (9)

в) P=0,Q=0,R=z  (10)

(8)+(9)+(10)=

Лк.12 элементы теории поля

12.1 Теор. Поля , осн. Понятия и определения.

Опр.1 Полем наз. Некоторая плоская или пространственная область, в каждой точке которой (определено ) значение некоторой величины.

Если каждой т.М этой области соответствует определенное число, то говорят что в этой области задано скалярное поле(СП).

Если же каждой точке М этой области соответствует некоторой вектор, то в этой области задано векторное поле(ВП).

Вектор = (М)

Число U=U(М)

Из этого следует ,что задание скалярного поля сводится к заданию числовой ф-ции двух переменных U=U(М) или трех переменных U=U(x,y,z)

Задание векторного поля = (М) сводится к заданию проекций а_х ,а_y , a_z вектора а на координатные оси, при этом эти проекции являются ф-циями координат т.М с которой данная векторная величина связана, иными словами, задание ВП равносильно заданию векторной ф-ции:

=(М)=( а_х ,а_y ,a_z)=(P,Q,R)=P(x,y,z) + Q(x,y,z) +

R(x,y,z) (1)

(1)- векторная ф-ция координат точки.

Примерами СП являются:

Поле температур, атмосферного давления, электр. потенциала.

Примерами ВП явл.: поле силы тяготения, поле скоростей, магнитное поле.

Опр.2 Если ф-ции U(M)( (M)) не зависят от времени , то СП(ВП) наз. стационарным (установившимся), если же поле меняется с течением времени , то оно наз. не стационарным (установившимся).

Далее будут рассмотрены только стационарные поля и будем считать ,что ф-ции U(M)-задающая СП и P(M),Q(M),R(M)-задающие ВП- непрерывны вместе со своими ЧП первого порядка.

12.2 Скалярное поле.

Рассм. СП задаваемое скалярной ф-цией U=U(x,y,z) (U=U(x,y)) для наглядного изобр.СП применяют поверхности(линии) уровня.

Опр.3 Поверхностью (линии) уровня СП определяемого ф-цией U(x,y,z) (U(x,y)), наз. геометр. место точек в которых рассматриваемая ф-ция принимает постоянное значение. Уравнения поверхности (линии уровня) имеют вид U(x,y,z)=с (U(x,y)=с), где с-const.

Пример

Найти ур-я поверхностей уровня, СП определяемой ф-цией U= , U(x,y,z)=c==> U==c

|c|<=1 1-x²-y²-z² = c²

x²+y²+z² =1- c² т.о. поверхностями уровня заданной ф-ции явл. семейство концентрических сфер с центром в начале координат.

Покажем, что всякое СП порождает некоторое векторное.

Из теор. Ф-ций нескольких переменных известно, что градиентом ф-ции U(x,y,z) (скалярного поля U(x,y,z)) в т.М наз. вектор корд. Которого являются значения ЧП(частных производных) заданной ф-ции в рассматриваемой точке.

Дельта-(δ)

grad U=( , , )= + +

Также известно, что производная т. U , по заданному направлению ℓ определяемому формулой:

ℓ=l

= cos α+cosβ + cosγ , (2)

cos α, cosβ , cosγ -направление cos направление ℓ.

Производная по направлению характеризует скорость изменения ф-ции в точке в заданном направлении ℓ :

если >0, тогда ф-ция (СП) в зад. направлении ↑

<0, то ф-ция U в задан.направлении. ↓

П усть ℓ⁰ - единичный вектор заданный направл.ℓ, тогда

ℓ ⁰= (cos α, cosβ , cosγ)

Тогда формулу (2) можно записать :

=grad U *ℓ⁰ =|grad|*|ℓ⁰ |*(cos gradU,ℓ⁰)=|grad|*cosφ (3)

Из формулы (3) видно, что достигает своего наибольшего значения когда cosφ равен 1 (φ=0), иными словами произв. достигает своего наибольшего значения когда направление вектора grad совпадает с направлением дифференцирования , и это наибольшее

Равно:

max =|grad U|=корень из след. выражения ()²+()² + ()²

Т.о. grad СП U указывает направление наибольшего возрастания ф-ции (поля). Всякое СП U(M) порождает ВП grad U(M)

grad- векторная характеристика скалярного поля.

Осн. Свойства:

1)grad ф-ции в каждой точке ┴ линии (поверхности) уровня проходящей через заданную точку.

2) grad(U±V)= grad U ± grad V

3) grad(c*V)= c grad ,c - const

4) grad (U*V)=grad U*V+ UgradV

5)grad (U/V)=(gradU*V-UgradV)/V²

6)grad(f(U))=f 'U*gradU

Каждое из этих свойств доказано на основании определения grad/

Доказательство 2)grad(U+V)=gradU+gradV

grad(U+V)= (U+V) +(U+V) +(U+V) =

(+)+(+)+(+)