
- •Л.1 двойной интеграл в декатовых координатах.
- •1.1 Основные понятия и определения
- •1.2 Геометрический и физический смысл дви.
- •1.3 Основные свойства дви
- •1.4 Вычисление дви в декартовых координатах
- •Л.2 дви в полярных координатах. Замена переменных в дви.
- •2.1 Замена переменных в дви.
- •2.2 Дви в полярных координатах.
- •Лекция №3 Геометрические и физические приложения дви.
- •3.1 Геометрические приложения дви.
- •1) Вычисление объёмов пространственных тел.
- •2) Вычисление s плоской фигуры:
- •3.2 Физические приложения двойных интегралов.
- •1.Масса. Вычисление массы плоской фигуры.
- •2.Вычисление статических моментов и координат центра тяжести(центра масс) пластины.
- •3. Вычисление моментов инерции пластины.
- •Лекция 4 тройной интеграл
- •4.2 Основные св-ва три
- •4.3 Вычисление три в декартовых координатах
- •Л.5 криволинейные интегралы по координатам II рода – кри-II
- •5.1 Основные понятия и определения кри-II, теорема существования
- •5.2 Основные свойства кри-II
- •Л. 6. Связь между дви и кри. Свойства кри II-го рода связанные с формой пути интегрирования.
- •6.2. Условия (критерии) равенства нулю контурного интеграла.
- •6.3. Условия независимости кри от формы пути интегрирования.
- •Лекция №7 Условия независимости кри 2-го рода от формы пути интегрирования (продолжение)
- •Л.8 Геометрическая и физические приложения кри 2-го рода
- •8.1 Вычесление s плоской фигуры
- •8.2 Вычисление работы переменой силы
- •Лекция№9 Поверхностные интегралы по площади поверхности (пви-1)
- •9.2. Основные свойства пви-1
- •9.3.Гладкие поверхности
- •9.4.Вычисление пви-1 свидением к дви.
- •Л.10. Поверхностные интегралы по координатам (пви-2)
- •10.3. Основные свойства пви-2.
- •10.4. Вычисление пви-2
- •11.1.Формула Остроградского-Гаусса.
- •11.2 Формула Стокса.
- •11.3. Применение пви к вычислению объёмов тел.
- •Лк.12 элементы теории поля
- •12.1 Теор. Поля , осн. Понятия и определения.
- •12.2 Скалярное поле.
- •Лк 13. Векторное поле (вп) и его характеристики.
- •13.1 Векторные линии и векторные поверхности.
- •13.2 Поток вектора
- •Опр 3.Потоком вектора через поверхность s в заданном направлении наз. Пви от скалярного произведения вектора поля на единичный вектор нормали к поверхности s и обозначается п.
- •13.3 Дивергенция поля. Формула Остроградского-Гаусса.
- •13.4 Циркуляция поля
- •13.5 Ротор (вихрь) поля.
- •14. Специальные векторные поля и их характеристики
- •14.1 Векторные дифференциальные операции 1 порядка
- •Произведение на скалярную функцию равно градиенту этой функции: .
- •14.2 Векторные дифференциальные операции II – порядка
- •14.3 Соленоидальное векторное поле и его свойства
- •2.В соленоидальном поле поток вектора поля через замкнутую поверхность s равен 0
- •14.4 Потенциальное (безвихревое) вп и его свойства
- •14.5 Гармоническое поле
- •Л.15 элементы функции комплексного переменного. Комплексные числа(к/ч).
- •15.1. К/ч определение, геометрическое изображение.
- •15.2 Геометрическое представление к/ч.
- •15.3 Операция над к/ч.
- •15.4 Понятие расширенной комплексной z-пл.
- •16.1.Последовательность комплексных чисел определение, критерий существования.
- •16.2Арифметические свойства приделов комплексных чисел.
- •16.3 Функция комплексного переменного: определение, непрерывность.
- •Л.17 Основные элементарные ф.-ции комплексного переменного (фкп)
- •17.1.Однозначные элементарные фкп.
- •Л.18 Дифференцирование фкп. Аналитическая ф-ия
- •18.1. Производная и дифференциал фкп: основные понятия.
- •18.2. Критерий дифференцируемости фкп.
- •18.3. Аналитическая функция
- •Л. 19 интегральное исчесление фкп.
- •19.2(О существов.Ифкп)
- •19.4 Теорема(интегральная ф-я Коши)
- •19.5Теорема(обобщенная ф-ла Коши)
- •Л.20. Геометрический смысл модуля и аргумента производной. Понятие о конформном отображении.
- •Л.21. Ряды в комплексной области.
- •21.2 Числовые ряды (чр):
- •21.2 Степенные ряды (ср):
- •21.3 Ряд Тейлора:
- •21.4 Ряд Лорана:
- •Содержание
- •1.1 Основные понятия и определения
- •1.2 Геометрический и физический смысл дви.
Л.18 Дифференцирование фкп. Аналитическая ф-ия
18.1. Производная и дифференциал фкп: основные понятия.
Определение производной ФКП не отличается от аналогичного определения производной ф-ии действительного переменного.
Рассмотрим однозначную ф-ию w=f(z). Пусть z=x+iy – некоторая точка, z є D(f). Выполним следующие действия:
А) дадим Х и У приращения ∆Х и ∆У, тогда и переменная Z получит приращение ∆Z=∆Х +i∆У;
Б) найдем соответствующие приращения ф-ии w=f(z): ∆W=f(Z+∆Z) – f(Z);
В) составим ∆W / ∆Z;
Опр_1. Если существует конечный предел отношения приращения ∆W ф-ии к приращению ∆Z при условии что ∆Z -> 0 произвольным образом, то этот предел назыв. Производной ф-ии w=f(z) и обозначается w’.
Таким образом, f `(z)=lim∆Z->0∆W / ∆Z (1)…
Замечание: в равенстве (1) z -> 0 произвольным образом, т.е. точка ∆Z+Z приближается к Z по любому из бесконечного множества направлений.
Опр_2. Если ф-ия w=f(z) имеет в т. Z производную, то она называется дифференцируемой в этой точке, а выражение f `(z) ∆Z назыв. Дифференциалом ф-ии w=f(z).
Основные свойства производной ФКП:
-
f
(kf)` = k(f)`;
(f±g)`= f `± g`;
(f g)` = f `g + f g`;
f(z) ` f `(z) g(z) – f(z)g`(z)
g(z) g2(z)
(z)=const => f `(z)=0 -
f
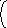
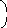
=
`(z) и g `(z) =>
-
w=f(g(z)) => w ` = (f(g(z)) ` = f `g g`z;
-
w=f(z): z=f -1 (w) => 1 / f `(w), f `(w)≠0.
18.2. Критерий дифференцируемости фкп.
Любую ФКП можно представить в виде w=f(z)=
=f(x+iy)=U(x,y)+iV(x,y), где U(x,y) – Re w
V(x,u) – Im w
∆w=f(x+iy)-f(z)=(U(x+∆x),(y+∆y))+iV(x+∆x),(y+∆y))-
-
(U(x,y)+iV(x,y))=(U(x+∆x),(y+∆y)-U(x,y))+
+i(V(x+∆x),(y+∆y)-V(x,y))= ∆U + ∆V.
f `(z)=lim∆x->0∆w/∆z = lim∆x->0(∆U + i∆V)/( ∆x + i∆y) (2).
Пусть ф-ия ∆w=f(x) имеет производную в точке z. Тогда предел (2) согласно определению производной не зависит от направления при котором т. Z+∆Z -> Z. А если это так, то считаем, что т. Z+∆Z приближается к т. Z по прямой параллельной оси ОХ, тогда f `(z)=lim∆x->0(∆U+i∆V) / ∆x = lim∆x->0(∆U/∆x + i∆V/∆y) = lim∆x->0∆U/∆x + lim∆x->0i∆V/∆y = ∂U/∂x+ +i∂V/∂х (3)…
Если же т. Z+∆Z приближается к т. . Z по прямой, параллельной оси ОУ, тогда . ∆Z = ∆У, ∆Х=0.
f `(z)=lim∆y->0(∆U+i∆V)/ i∆у = lim∆y->0(∆V/∆y + ∆U/i∆y) = lim∆y->0∆V/∆y – i lim∆y->0i∆U/∆y = ∂V/∂y - i∂U/∂y (4).
Т
∆U/∆x
= ∆V/∆y
∆V/∆x
= - ∆U/∆y
 ак
как пределы (3) и (4) должны быть равны, то
ак
как пределы (3) и (4) должны быть равны, то
∂U/∂x+ +i∂V/∂х = ∂V/∂y - i∂U/∂y =>
Теорема 18.1. (Критерий дифференц. ф-ии в т.)
∆U/∆x
= ∆V/∆y
∆V/∆x
= - ∆U/∆y
 Если ф-ия ∆w=f(x)
определена в т. Z=x+iy
и некоторой её окрестности, то для
дифференцируемости ф-ии ∆w=f(x)
в т. Z
необходимо и достаточно, чтобы в этой
точке существовали ч/п функций U(x,y)
и V(x,y)
и выполнялись следующие условия:
- условия КРЭДА (5).
Если ф-ия ∆w=f(x)
определена в т. Z=x+iy
и некоторой её окрестности, то для
дифференцируемости ф-ии ∆w=f(x)
в т. Z
необходимо и достаточно, чтобы в этой
точке существовали ч/п функций U(x,y)
и V(x,y)
и выполнялись следующие условия:
- условия КРЭДА (5).
Следствие: если условие КРЭДА выполняется, то производную ФКП можно найти по одной из четырёх формул:
f `(z)= ∆U/∆x + i∆V/∆x = ∆V/∆y + i∆V/∆x =
= ∆U/∆x - i∆U/∆y = ∆V/∆y - i∆U/∆y
Пример: (еz)z = ez
W(z)=ez = ex(cosy + isiny) = ex cosy +iex siny
U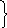
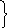 (x,y)
= ex
cosy U’x=excosy,
V’x=exsiny
=>
(x,y)
= ex
cosy U’x=excosy,
V’x=exsiny
=>
V(x,y) = ex siny U’y=ex siny, V’y=ex cosy =>
-
U’x=V’y => w = ez
-
U’y=V’x
Следовательно, f ‘(z)=U’x+iV’x = excosy + iexsiny =
= ex (cosy +isiny) = ex
Теорема 18.2.
Все основные элементарные ФКП дифференцируемы во всех точках своей области определения.
