
- •7. Как определяется операция умножения матрицы а на число λ? Приведите пример. Как связаны определители квадратных матриц а и λА размера nxn? Ответ обоснуйте.
- •10. Дайте определение ранга матрицы. Приведите примеры матриц третьего порядка рангов 1, 2 и 3. Что можно сказать об определителе произвольной матрицы размера nxn ранга n? Ответ обоснуйте.
- •8. Сформулируйте правило Крамера для решения систем линейных уравнений. Приведите пример применения правила Крамера для системы линейных уравнений от трех переменных.
- •17. Докажите что множество решений однородной системы линейных уравнений является линейным пространством. Как найти размерность этого пространства.
- •39. Дайте определение ортонормированной системы векторов.
- •9. Сформулируйте правило Крамера для решения систем линейных уравнений. Докажите правило Крамера для системы линейных уравнений от двух переменных.
- •24. Дайте определение линейного пространства. Приведите примеры линейных пространств, отличных от арифметических пространств Rn.
- •25. Дайте определение базиса линейного пространства. Приведите пример. Докажите однозначность разложения вектора по базису.
- •31. Дайте определение подпространства линейного пространства и приведите пример. Как связаны размерности пространства и его подпространства? Ответ обоснуйте.
- •33. Дайте определение линейного пространства. Докажите, что симметрические матрицы порядка 2 образуют линейное пространство. Найдите его размерность.
- •42. Дайте определение скалярного произведения в Rn. Неравенство Коши-Буняковского.
- •44. Дайте определение фундаментального набора решений однородной слау
- •47. Могут ли фундаментальные наборы решений однородной слау различаться а) числом решений? Ответы обосновать.
- •52. Собственные значения и собственные векторы матрицы.
- •63.Матрица линейного оператора.
- •68. Квадратная матрица a называется ортогональной
- •108. Кривые второго порядка.
1. Укажите, какие из равенств не выполняются для любых матриц А, В, С (предполагается, что все произведения определены): а) АВ = ВА; б) (АВ)С = А(ВС); в) (АВ)Т = ВТ * АТ; г) (АВ)Т = АТ *ВТ. Приведите примеры, опровергающие неверные равенства.
Определение: Матрица – прямоугольная таблица чисел. Отдельные числа (или символы, их заменяющие) называют элементами матрицы.
a11 a12 …a1n
a21 a22 …a2n
…
an1 an2 …ann
mxn – порядок матрицы.
Свойства сложения.
1.Ассоциативность:А+(В+С)=(А+В)+С
2. Коммутативность: А+В=В+А.
3. А+0=А.
Разность матриц: А-В = А+(-1)В
Свойства умножения матриц:
Если матрицы А, В и С таковы, что их произведение возможно, то
1. (АВ)С = А(ВС)
2. А(В+С)=АВ+АС
3. (В+С)А=ВА+СА
4.
![]()
5.
![]() – умножение матриц не обладает свойством
коммутативности.
– умножение матриц не обладает свойством
коммутативности.
Не выполняется АВ=ВА, пример: А – матрица порядка 2х2, В порядка 2х3, в этом случае АВ не равняется ВА, т.к. ВА не существует.
A
=
![]() , B
=
, B
=
![]() ,
,
то
AB
=
![]() , а BA
=
, а BA
=
![]()
Не выполняется АВт = Ат *Вт, пример: А – матрица порядка 2х2, а В порядка 2х3, в этом случае АВт не равняется Ат*Вт, т.к. Ат*Вт не существует.
Остальные равенства выполняются для любых матриц АВС.
3. Дайте определение произведения матриц А и В. Приведите пример, когда АВ существует, а ВА – нет. Существуют ли ненулевые квадратные матрицы А и В такие, что АВ = 0? Ответ обоснуйте.
Пусть
даны матрицы
![]() и
и
![]() .
.
![]() *
*![]() =
=
![]()
Получаем матрицу С, каждый элемент которой равен сумме произведений элементов i–ой строки А на соотв. элемент j–го столбца В.
1)
Произведение А
* В определено,
если s
= m
(число столбцов А
равно числу строк В).
Если
![]() ,
то произведение
,
то произведение
![]() найти
нельзя.
найти
нельзя.
Чтобы оба произведения AB и BA не только были определены, но и имели одинаковый порядок, необходимо и достаточно, чтобы обе матрицы A и B были квадратными матрицами одного и того же порядка.
Например:
А 2 * 3 * В 3 * 4 - сущ. s = m
В
3 * 4
* А 2 * 3
– не сущ.
![]()
2) Если s = m, то матрица произведения A*B имеет порядок r*n.
3) Если произведение матриц определено, то С=АВ есть C=||cik||, где сik = скалярному произведению i строки А на k столбец В.
Существуют ненулевые квадратные матрицы А и В такие, что АВ = 0:
1 2 -2 -2
1 2 1 1
4. Дайте определение произведения матриц А и В. Существуют ли матрицы А и В такие, что АВ = 0, а ВА = Е? Ответ обоснуйте.
Пусть
даны матрицы
![]() и
и
![]() .
.
![]() *
*![]() =
=
![]()
Получаем матрицу С, каждый элемент которой равен сумме произведений элементов i–ой строки А на соотв. элемент j–го столбца В.
1)
Произведение А
* В определено,
если s
= m
(число столбцов А
равно числу строк В).
Если
![]() ,
то произведение
,
то произведение
![]() найти
нельзя.
найти
нельзя.
Чтобы оба произведения AB и BA не только были определены, но и имели одинаковый порядок, необходимо и достаточно, чтобы обе матрицы A и B были квадратными матрицами одного и того же порядка.
2) Если s = m, то матрица произведения A*B имеет порядок r*n.
3) Если произведение матриц определено, то С=АВ есть C=||cik||, где сik = скалярному произведению i строки А на k столбец В.
5. Дайте определения вырожденной и невырожденной квадратных матриц порядка 3. Приведите примеры таких матриц. Докажите, что ортогональная матрица является невырожденной.
Матрица А порядка n*n называется невырожденной, если ее строки линейно независимы, в противном случае – вырожденная.
Теорема: квадратная матрица А невырождена тогда и только тогда, когда ее определитель |А| не равен нулю.
|А|
=
 = -1
= -1
![]() 0 – невырожд.
0 – невырожд.
Квадратная матрица A называется ортогональной, если соответствующая ей система векторов столбцов является ортонормированной.
(ai,aj)=∑k=1nakiakj= δij
Пусть A - ортогональная матрица.
AT=A-1 –необходимое и достаточное условие ортогональности матрицы A.
ATA=E (по определению), A-1A=E.
А т.к. обратная матрица существует, если А невырожденная, то ортогональная матрица является невырожденной.
6. Приведите основные свойства определителей. Проверьте справедливость свойства |АВ|=|А|*|В| для матриц
А=
![]()
![]() и
В=
и
В=
![]()
![]()
Свойства определителей:
1. Если какая-либо строка определителя состоит из нулей, то и сам определитель равен нулю.
2. При перестановке двух строк определитель умножается на -1.
3. Определитель с двумя одинаковыми строками равен нулю.
4. Общий множитель элементов любой строки можно вынести за знак определителя.
5. Если элементы некоторой строки определителя А представлены в виде суммы двух слагаемых, то и сам определитель равен сумме двух определителей Б и Д. В определителе Б указанная строка состоит из первых слагаемых, в Д - из вторых слагаемых. Остальные строки определителей Б и Д - те же, что и в А.
6. Величина определителя не изменится, если к одной из строк прибавить другую строку, умноженную на какое угодно число.
7. Сумма произведений элементов любой строки на алгебраические дополнения к соответствующим элементам другой строки равны 0.
8. Определитель матрицы А равен определителю транспонированной матрицы Ат, т.е. определитель не меняется при транспонировании.
|A| = | 1 2| = 1+2 =3
|-1 1|
|B| = |a b| = ad – bc
|c d|
|A| |B| = 3 (ad – bc)
|AB| = | 1 2| |a b| = |a + 2c b + 2d| =
|-1 1| |c d| |-a + c -b + d|
= (a + 2c)(-b + d) + (a – c)(b + 2d) =
= - ab + ad – 2bc + 2cd + ab + 2ad – bc – 2cd = 3ad – 3bc = 3 (ad – bc)
7. Как определяется операция умножения матрицы а на число λ? Приведите пример. Как связаны определители квадратных матриц а и λА размера nxn? Ответ обоснуйте.
Произведением А на число λ называется матрица, каждый элемент которой равен произведению соответствующего элемента А на λ. Следствие: Общий множитель всех элементов матрицы можно выносить за знак матрицы.
10. Дайте определение ранга матрицы. Приведите примеры матриц третьего порядка рангов 1, 2 и 3. Что можно сказать об определителе произвольной матрицы размера nxn ранга n? Ответ обоснуйте.
Ранг матрицы – число линейно независимых столбцов или строк, содержащихся в данной матрице.

Число ненулевых диагональных элементов равно 2, следовательно, r(B)=2.
8. Сформулируйте правило Крамера для решения систем линейных уравнений. Приведите пример применения правила Крамера для системы линейных уравнений от трех переменных.
Пусть дана система АХ = В n линейных уравнений с n неизвестными. Если Aне равно 0, то система имеет единственное решение:x1=A1/ A ; x2=A2/ A , где Аi, Определители получаются из определителя|А| заменой соответствующего столбца столбцом свобод членов.
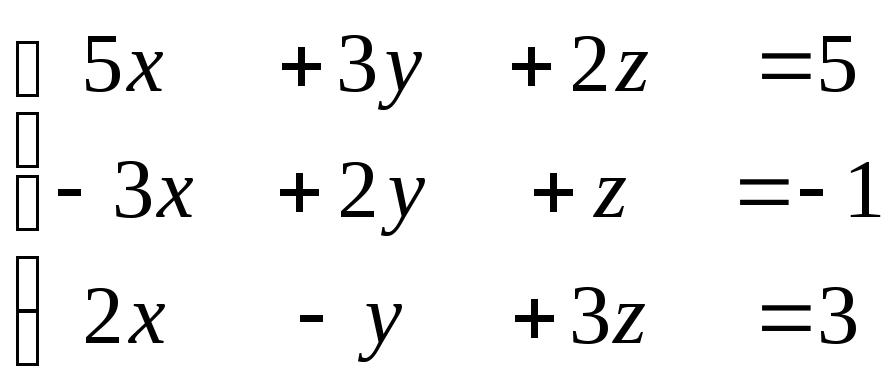
В виде матрицы эту систему можно записать таким образом :
A
=
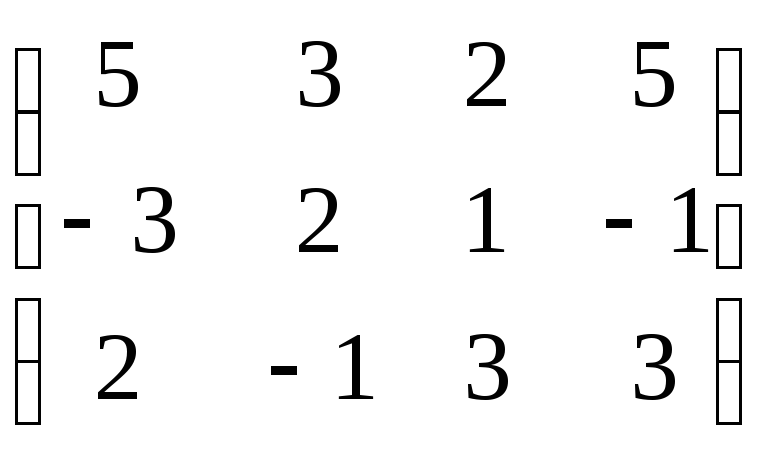 , где
, где
ответы будут уравнений будут находится в последнем столбце. Теперь мы введем понятие основного определителя; в данном случае он будет выглядеть таким образом :
![]() =
=
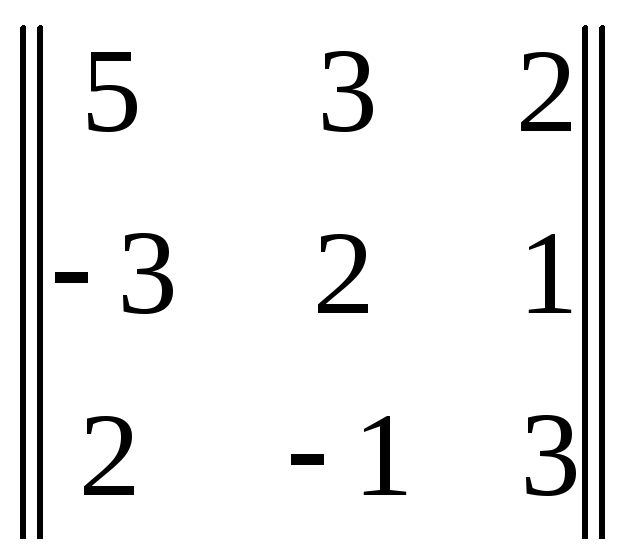 = 66 .
= 66 .
Основным определителем является матрица, составленная из коэффициентов стоящих при переменных. Они также идут в порядке столбцов, т. е. в первом столбце стоят коэффициенты, которые находятся при x, во втором столбце при y, и так далее. Это очень важно, ибо в следующих действиях мы заменяем каждый столбец коэффициентов при переменной на столбец ответов уравнений.
![]() 1
=
1
=
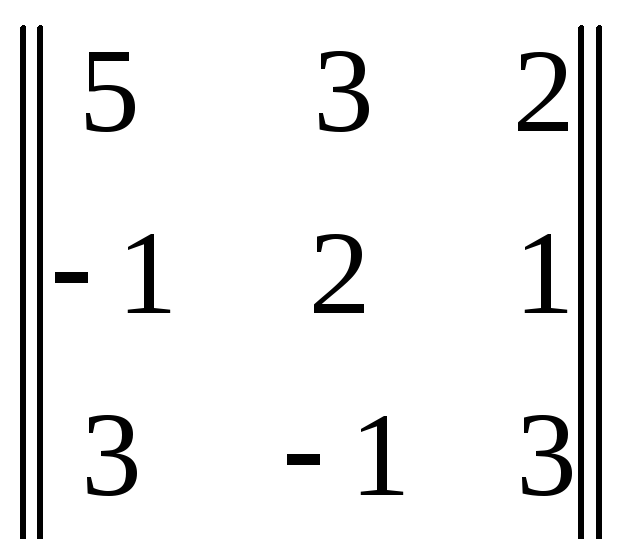 = 43,
= 43,
![]() 2
=
2
= = 41,
= 41,
![]() 3
=
3
=
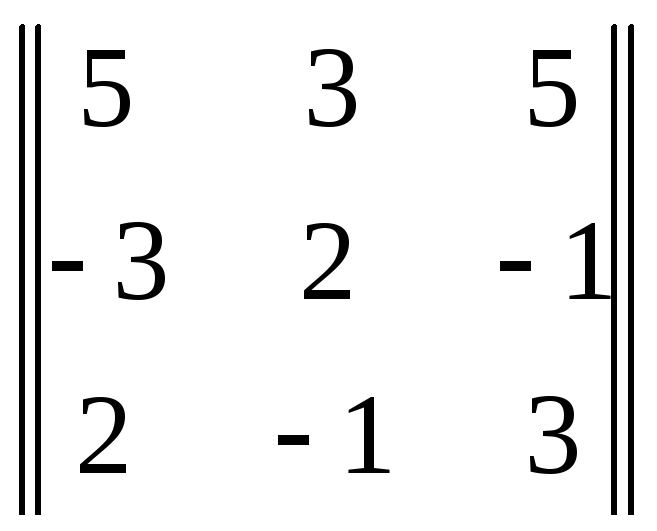 = 51.
= 51.
Затем
нужно найти определители
![]() 1
,
1
,
![]() 2
,
2
,
![]() 3
и применить правило Крамера. Оно выглядит
так :
3
и применить правило Крамера. Оно выглядит
так :
x1
=
![]() =
=
![]() ,
,
x2
=
![]() =
=
![]() ,
,
x3
=![]() =
=![]() – для данного
случая, а в общем виде оно выглядит
следующим образом : xi
=
– для данного
случая, а в общем виде оно выглядит
следующим образом : xi
=
![]() .
.
17. Докажите что множество решений однородной системы линейных уравнений является линейным пространством. Как найти размерность этого пространства.
Множество V называется линейным векторным пространством, если в нем определены операции сложения и умножения на число: а+b=b+a (коммутативности), (a+b)+c=a+(b+c) (aссoциативности), сущ-ет нулевой вектор, такой, что если его прибавить к исходному вектору, то получится исходный вектор a+0=a , наличие противоположного вектора в сумме с исходным дающий ноль-вектор а+(-а)=0, (a+b)=ka+kb(дистрибутивность), (k+l)a=ka+la, k(la)=(kl)a, 1a=a и подчиняющиеся 8 аксиомам.
Примерами лин. пространств могут служить арифметическое n-мерное векторное пространство Rn, пространство решений произвольной однородной СЛАУ, множество многочленов степени не превышающей n. Например, линейным является пространство подмножества векторов х=(х1,х2,х3,
38. Какие векторы называются ортогональными? Докажите, что ортогональное дополнение к ненулевому вектору v в R5 является линейным подпространством размерности 4.
Два вектора aˉ и bˉ называются ортогональными, если их скалярное произведение равно 0. аˉbˉ, если аˉbˉ=0.
