Лебедев КММФЯ / modelirovanie_nanostruktur_2013

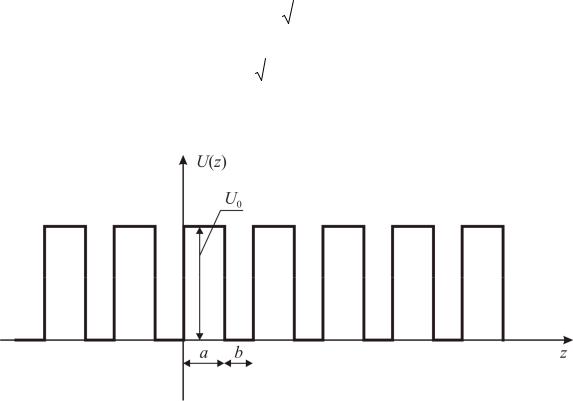
		21
0,	если nc z nc a	(2.5)
U z	,
U	,если nc a z n 1 c
0

где a — ширина ямы, b — ширина барьера, c a b — постоянная кри-

сталлической решетки, U0 — высота барьера,

n 0, 1, 2, . Решения

уравнения Шредингера (2.1) при E U0 могут быть записаны в виде:

A ej z nc

B e j z nc ,

если nc z nc a

n

n

n

, (2.6)

z

z nc a

z nc a

Dne

,

если

nc a z n 1 c

Cne

где

1

,

(2.7)

2mnE

1

,

(2.8)

2mn U0

E

mn — эффективная масса электрона в кристалле, j — мнимая единица.

Рис. 2.1. Потенциальный рельеф для электрона в кристалле (модель Кронига–Пенни).

Из граничных условий (2.2), принимая во внимание постоянство эф-

фективной массы во всем кристалле, получаем следующую систему алгеб-

раических уравнений:

22 Компьютерное моделирование микро и наноструктур

A B C		e b D			n 1	e b	,
n n		n 1
j A j B C			e b D				e b ,
n	n		n 1				n 1	(2.9)
A ej a B e j a			C		D ,
				n
n	n					n

j Anej a j Bne j a Cn Dn .

При этом между коэффициентами Cn 1,Dn 1 и Cn ,Dn существует связь, вытекающая из связи между волновыми функциями n 1 и n . Так как функции n 1 и n являются решениями одного и того же уравнения Шредингера, то они могут отличаться друг от друга только постоянным множителем, квадрат которого равен единице. То есть:

n n 1ej ,

где — некоторый вещественный параметр.

Отсюда

Cn 1 Cne j ,

Dn 1 Dne j .

(2.10)

(2.11)

Подставляя значения (2.3) в систему уравнений (2.0.), получим сис-

тему из четырех однородных уравнений с четырьмя неизвестными An, Bn ,

Cn и Dn . Для того, чтобы эта система имела нетривиальное решение, не-

обходимо, чтобы определитель, составленный из коэффициентов этих уравнений, был равен нулю. Записав и раскрыв определитель, получим уравнение, определяющее значения энергии электрона E (входящей в вы-

ражения для и ), для которых существуют нетривиальные решения системы (2.0.):

	cos a cosh b	2 2	sin a sinh b cos .	(2.12)
		2

Анализ уравнения (2.4) затруднен тем, что энергия входит в и ,

однако его можно упростить, представив потенциал в ещё более идеализи-

23

рованном виде. Произведение b определяет степень прозрачности по-

тенциального барьера для электронов, в него входит ширина барьера b и

высота барьера U0 . Рассмотрим случай, когда ширина барьера устремля-

ется к нулю, а высота — к бесконечности, причем так, что произведение

	U0b остается постоянным. При этом,		так как U0 ~ 2, то при			b 0 и
	U0 произведение b 0. Тогда, вводя обозначение
	P lim		2ab		,	(2.13)
			2
	b 0
	U0
	U0b const
	от уравнения (2.4) перейдем к более простому:
	cos a P	sin a		cos .		(2.14)
		a

Уравнение (2.5) называется уравнением Кронига–Пенни. Параметр P

пропорционален площади потенциального барьера; он характеризует сте-

пень прозрачности барьера для электронов или степень связанности элек-

трона внутри потенциальной ямы.

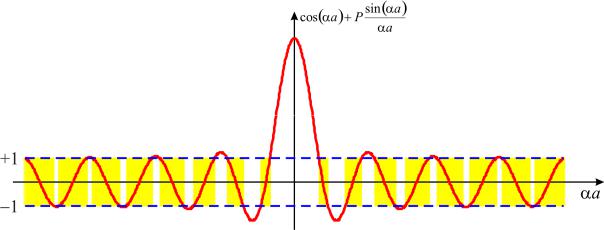
Для анализа уравнения (2.5) изобразим графически его левую часть как функцию аргумента a (рис. 2.2, сплошная линия). Действительные корни этого уравнения существуют только при тех значениях a, при ко-

торых левая часть уравнения принимает значения в интервале 1;1 . На рис. 2.2 заштрихованы области допустимых значений a. Их ширина за-

висит от параметра P: чем он меньше, тем они шире и при фиксированном значении P становятся шире с увеличением a, а значит и энергии.

24	Компьютерное моделирование микро и наноструктур

Рис. 2.2. Графический анализ уравнения Кронига–Пенни.

Таким образом, энергия электрона в периодическом поле не может принимать любое значение, как для свободного электрона. Она ограничена рядом полос (зон) разрешенных значений, отделенных друг от друга за-

прещенными зонами — энергетический спектр электрона в периодическом поле имеет зонную структуру. Ширина разрешенных зон определяется степенью связанности электрона внутри потенциальной ямы.

Задания для компьютерного моделирования.

1.Изобразить графически левую часть уравнения (2.5), схематически изобразить на получившемся графике зоны разрешенных и запре-

щенных значений a. Проиллюстрировать, как изменяется ширина разрешенных зон при изменении параметра P.

2.Проанализировать два крайних случая: P 0 (электрон совершенно свободен) и P (барьер совершенно непроницаем, электрон за-

перт в пределах одной потенциальной ямы).

Примечание: пример программы для среды MathCAD приведен в Приложении 1.

25

2.2. Моделирование энергетического спектра электрона в

одномерной квантовой яме

Если сформировать тонкий слой узкозонного материала между дву-

мя достаточно толстыми слоями широкозонного материала, то для элек-

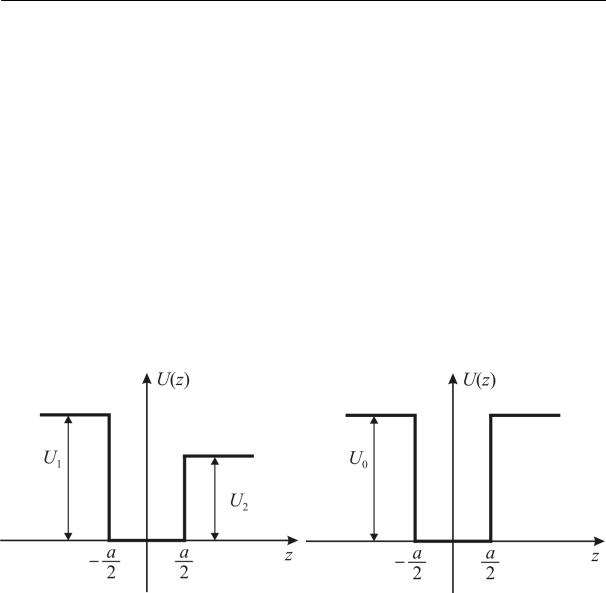
трона, движущегося в поперечном к плоскостям слоёв направлении, может быть сформирован потенциальный рельеф, изображенный на рис. 2.3 (энергия отсчитывается от дна зоны проводимости материала ямы). Такого рода рельеф носит название прямоугольной потенциальной ямы. В данном разделе мы будем рассматривать симметричную потенциальную яму

(рис. 2.3, б).

а

б

Рис. 2.3. Энергетическая диаграмма прямоугольной потенциальной ямы: а – несим-

метричной, б – симметричной.

2.2.1. С бесконечно высокими стенками

Рассмотрение начнем с идеализированного случая потенциальной ямы с бесконечно высокими стенками. В этом случае вне ямы функция

(z,E) тождественно равна нулю, а внутри ямы удовлетворяет уравнению Шредингера вида

26 Компьютерное моделирование микро и наноструктур

	2		2 (z,E)				E (z,E)		(2.15)
	2m		z	2
с граничными условиями
					a
						,E		0,	(2.16)
				2

где a — ширина потенциальной ямы (толщина среднего слоя рассматри-

ваемой трехслойной структуры). Тогда a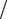2 — координаты интерфейсов между слоями.

Из математической физики известно [20], что уравнение (2.0.) имеет решение лишь при дискретных значениях энергии E — собственных зна-

чениях данного уравнения:

E	2				2
					.	(2.17)
			a
	2m

Система обладает симметрией по оси Oz относительно начала коор-

динат, поэтому совокупность собственных решений уравнения Шрединге-

ра (2.0.) разбивается на подгруппы четных и нечетных решений:

Ccos					, если 1,3,5,
			a			(2.18)
z,E
Csin				, если 2,4,6,
			a

Здесь C — нормировочный коэффициент.

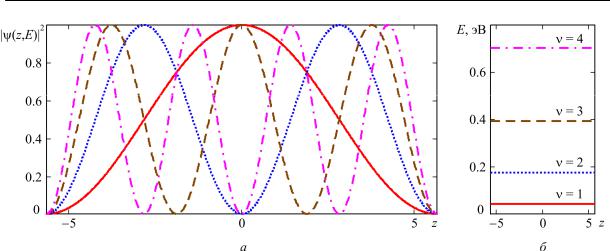
Графики огибающих волновых функций электрона в квантовой яме шириной 20 атомных монослоёв (11.3 нм) для первых четырех разрешен-

ных уровней энергии представлены на рис. 2.4, а, а энергетический спектр электрона в такой яме — на рис. 2.4, б. Материал ямы — GaAs.

27

Рис. 2.4. Огибающие волновых функций (а) и квантованные уровни энергии (б) элек-

трона в прямоугольной квантовой яме.

Задания для компьютерного моделирования.

1.Построить огибающие волновых функций и квантованные уровни энергии в прямоугольной квантовой яме с бесконечно высокими стенками для различных значений ширины ямы: 10, 20 и 30 атомных

монослоёв GaAs.

Примечание: пример программы для среды MathCAD приведен в Приложении 2.

2.2.2. Со стенками конечной высоты

В реальном случае стенки потенциальной ямы имеют конечную ши-

рину, и для симметричной потенциальной ямы потенциал U z в уравне-

нии (2.1) имеет вид:

		если		z			a
0,								,
							2	(2.19)
U z
							a
U	0	, если	z					.
							2

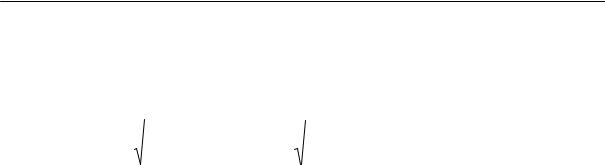
Решения уравнения Шредингера (2.1) записываются отдельно в каж-

дой из трех областей, где потенциал U z постоянен, в виде:

28 Компьютерное моделирование микро и наноструктур

			1	z Ae z ,
				1
			2	z A ej z					B	e j z ,		(2.20)
				2					2
			3	z B e z.
				3
Здесь		2mB U0 E				,		2mAE			, mA и mB	— эффективные
		2
									2

массы электронов в материале A, образующем яму, и в материале B, обра-

зующем барьеры, соответственно. Решения 1 и 2 записаны с учетом того, что они должны равняться нулю на бесконечности. Значения кон-

стант A1, A2, B2 и B3 находятся из граничных условий (2.2), которые по-

сле подстановки туда решений (2.7) принимают вид:

a

j

a

B

j

a

,

A e 2

A e 2

e 2

1

2

2

e

a

j

e j

a

j

ej

a

A

A

B

,

2

2

2

2

1

mB

2

mA

mA

(2.21)

a

a

a

j

j

,

A e 2

B e 2

B e 2

2

2

3

j

j

a

j

j

a

a

A

e

2 B

2

e 2

B

e 2 .

2

mA

mA

3

mB

Система алгебраических уравнений (2.8) имеет нетривиальное ре-

шение тогда и только тогда, когда её определитель равен нулю:

a

j

a

j

a

e 2

e 2

e 2

0

a

j

j

a

j

j

a

e

2

e 2

e 2

0

m

m

m

0.

(2.22)

Det

B

A

a

A

a

a

0

j

j

e

2

e

2

e

2

j

j

a

j

j

a

a

0

e

2

e

2

e

2

mA

mA

mB

Раскрывая определитель и упрощая полученное выражение, прихо-

дим к уравнению

29

2mA2 sinh j a 2 j mAmB cosh j a 2mB2 sinh j a 0, (2.23)

определяющему разрешенные значения энергии электрона в квантовой яме. Уравнение (2.9) является трансцендентным и требует численного или графического решения.

Система (2.8) имеет бесконечное множество решений, отличающих-

ся друг от друга произвольным множителем. Выражая из этой системы константы A2, B2 и B3 через A1, получим частное решение в виде:

1

mA

j

a

A A

1 j

e

2 ,

2

1

2

mB

1

mA

j

a

B

2

A

1 j

e

2 ,

(2.24)

1

2

mB

1

mA

j a

1

mA

j a

B3 A1

j

.

2

1

e

2

1 j

e

mB

mB

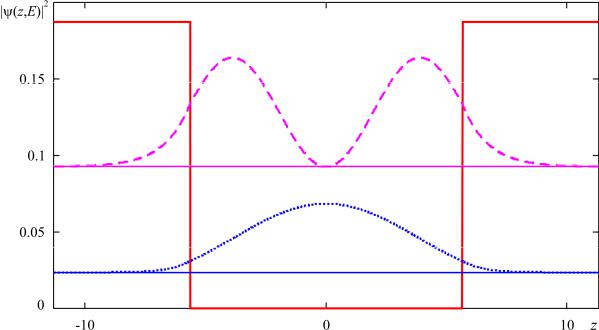
Графики огибающих волновых функций электрона в квантовой яме шириной 20 атомных монослоёв (11.3 нм) для первых трех разрешенных уровней энергии, рассчитанных из уравнения (2.9), представлены на рис. 2.5. Графики схематично наложены на зонную диаграмму гетеропере-

ходов, образующих квантовую яму, при этом начала отсчета по оси орди-

нат для графиков огибающих волновых функций совмещены с соответст-

вующими значениями энергии на зонной диаграмме. Материал ямы —

GaAs, материал барьеров — Al0.3 Ga0.7 As.

30	Компьютерное моделирование микро и наноструктур

Рис. 2.5. Огибающие волновых функций и квантованные уровни энергии электрона в прямоугольной квантовой яме со стенками конечной высоты.

Как видно из рис. 2.5, в областях барьеров имеется определенная,

хоть и весьма малая, вероятность нахождения электрона, то есть электрон,

преимущественно локализованный в квантовой яме, проникает и в области барьеров.

Задания для компьютерного моделирования.

1.Построить огибающие волновых функций и квантованные уровни энергии в прямоугольной квантовой яме, образованной слоем GaAs,

заключенным между слоями Al0.3 Ga0.7 As, для различных значений ширины ямы: 10, 20 и 30 атомных монослоёв.

2.Сравнить положения энергетических уровней в такой квантовой яме

с энергетическими уровнями бесконечно глубокой квантовой ямы.

Примечание: пример программы для среды MathCAD приведен в Приложении 3.