1.3. Количественная мера информации для разновозможных событий (сообщений). Энтропия источника дискретных (цифровых) сообщений

Формула (1.2), , устанавливает непосредственную связь между количеством информации, получаемой о некотором i-м событии (x_i) в результате опыта, и изменением вероятности этого события до (p(x_i)) и после (p_c(x_i)) опыта.

Эта связь может быть обобщена и на случай, когда имеется некоторое конечное множество независимых событий x_i с разными априорными вероятностями p(x_i). Такие события называют разновозможными событиями. Указанную зависимость получил Клод Шеннон, существенно развивший количественную меру информации соотечественника Р. Хартли.

Рассмотрим некоторое конечное множество событий . Такими событиями могут быть, например, состояния регистра данных компьютера. Допустим, что эти события независимы и несовместны. Независимость означает, что наступление одного события не зависит от того, было или не было до этого другое событие. Несовместность означает, что разные события не могут происходить одновременно. Например, после аналого-цифрового преобразования (АЦП) происходит запись результата, представляющего собой двоичное n-разрядное число в регистр. Регистр не может находиться одновременно в двух разных состояниях, т.е. в него нельзя одновременно записать два разных числа.

Пусть априорные вероятности событий x_i соответственно равны . Для несовместных событий выполняется условие

.

Это означает, что в течение некоторого наблюдаемого отрезка времени всегда происходит лишь одно из этих событий.

Множество с известным распределением вероятностей его элементов будем называть ансамблем, который можно представить как

. (1.4)

Ансамбль (1.4) рассматривается как некоторая модель физической системы, которая может находиться в различных состояниях или в которой может происходить различных событий (вспомните ранее упомянутый регистр данных). В этой модели мы рассматриваем случай, когда эти события независимы и несовместны.

Используя формулу (1.2), можно сказать, что достоверное сообщение [] о том, что из всех событий происходит именно событие, несет в себе количество информации, равное

(1.5)

Из (1.5) следует, что сообщение о событии несет тем большее количество информации, чем меньше априорная вероятность этого события. Данное положение хорошо согласуется с интуитивным представлением об информации. Нас нисколько не удивит сообщение в разгар лета, что завтра ожидается теплый день. Неопределенность такого события ничтожно мала, и поэтому услышанное нами сообщение содержит очень мало нового – мало информации. Если бы мы вдруг услышали сообщение, что завтра ожидаются заморозки, то в этом сообщении (если оно, конечно, достоверно) для нас содержалось бы гораздо больше информации. Таким образом, формула (1.5) согласуется с нашими интуитивными представлениями.

Формула (1.5) указывает, что в конечном ансамбле Х сообщения x_i о разных событиях несут в общем случае разное количество информации. При решении большинства задач, связанных с построением систем передачи и преобразования информации, оказалось достаточным знать среднее количество информации, приходящееся на одно достоверное сообщение.

Среднее значение а_ср нескольких (n) случайных величин a₁, a_2,,…,a_n в соответствии с правилами теории вероятностей [Вентцель Е.С., Овчаров Л.А. Теория вероятностей и ее инженерные приложения. – М.: Высшая школа, 2010. – 480 с.] может быть определено как математическое ожидание (МО):

Пример. Имеется ряд чисел: 1, 1, 1, 4, 4, 7. Определить среднее значение.

Из арифметики вы знаете, что надо все сложить и поделить на общее количество чисел

.

А теперь запишем это в таком виде

На предыдущей лекции мы с вами определили, что называется отношение числа элементарных исходов, благоприятствующих данному событию, к числу всех равно­возможных исходов опыта, в котором может появиться это событие, есть вероятность события.

В нашем примере имеется 3 события: а₁ – появление числа «1» с вероятностью р(а₁)=3/6, а₂ – появление числа «4» с вероятностью р(а₂)= 2/6 и а₃ –появление числа «7» с вероятностью р(а₃)=1/6. Таким образом, можем записать выражение для среднего значения

,

т.е. получили приведенную выше формулу для МО.

В нашем случае случайными величинами являются частные меры количества информации , поэтому среднее количество информации, приходящееся на одно достоверное сообщение определяется как

.

С учетом формулы (1.5), определяющей , получим

. (1.6)

В данном случае является мерой количества информации, приходящейся в среднем на одно достоверное сообщение о событии при передаче и преобразовании большого числа таких сообщений.

Эту мера количества информации предложил К. Шеннон. Она более общая, чем мера Хартли, и получила название энтропии конечного ансамбля дискретных событий .

Пример вычисления . Вычислим энтропию двоичного канала как источника информации. В таком канале передаются два символа «0» и «1», т.е. ансамбль событий можно представить как

,

где событие соответствует символу «0», а событие – символу «1».

Обозначим для простоты записи , а [не забываем, что ^{], по формуле (1.6) находим}

(1.7)

Лк1_7-09-2018

Лк_2

Для построения графика зависимости от определим для трех значений :

Здесь имеется два вида неопределенности: в первом слагаемом при р=0, а во втором – при р=1 получаем log(0), который, как известно, не существует

Для раскрытия неопределенности для первого слагаемого выражения (1.7) при малых значениях рассмотрим предел, к которому стремится это слагаемое:

. Здесь – log p представлен как log 1 – log p.

Обозначив и воспользовавшись правилом Лопиталя, т.е. взяв производные по α от числителя и знаменателя, получим

.

Таким образом, при значении .

Нетрудно убедиться, что при , а при .

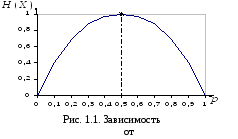
На рис. 1.1 приведен график зависимости от , полученный по формуле (1.7).

Из этого графика видно, что энтропия при и , имеет максимальное значение при . Эти результаты нетрудно объяснить: действительно, при априорно известно, что в канале передаются только символы «1», и сообщение об этом, т.е. их прием на выходе канала, не несет информации.

Аналогично при , когда в канале передаются только символы «0», сообщение не несет информации.

При символы «0» и «1» будут иметь одинаковую вероятность и наличие каждого из этих символов будет иметь наибольшую неопределенность. Поэтому достоверный прием на выходе канала конкретного символа будет полностью устранять эту неопределенность, и это сообщение, получаемое в результате приема, будет обеспечивать получение максимального количества информации: , т.е. в двоичном канале, когда вероятности обоих символов одинаковы, достоверный прием любого из них несет 1 дв. ед. информации.

В данном случае имеем равновероятные события, для которых справедлива мера Хартли: I=log₂2=1 дв.ед.