
- •Введение
- •1. Основные понятия. Количественная мера информации
- •Понятие информации
- •1.2. Количественная мера информации для равновозможных событий
- •1.3. Количественная мера информации для разновозможных событий (сообщений). Энтропия источника дискретных (цифровых) сообщений
- •1.4. Свойства энтропии источника дискретных сообщений
- •1.5. Энтропия источника совместных сообщений
- •1.6. Определение количества информации источника дискретных сообщений при неполной достоверности результатов опыта
- •1.7. Некоторые свойства количественной меры информации источника дискретных сообщений при неполной достоверности результатов опыта
- •1.9. Избыточность источника сообщений
- •1.10 Энтропия источника при наличии коррелятивных связей между двумя соседними символами
- •Контрольные вопросы
- •2. Информационные характеристики непрерывных (аналоговых) источников информации
- •2.1. Понятие о непрерывных (аналоговых) источниках информации
- •2.2. Энтропия непрерывного источника информации. Количество информации в одном замере непрерывной случайной величины
- •2.3. Примеры вычисления энтропии непрерывных источников информации
- •2.4. Количество информации, содержащееся в одном замере непрерывной случайной величины при неполной достоверности результатов измерения
- •Контрольные вопросы
- •3. Понятие о пропускной способности каналов и скорости передачи информации
- •3.1. Пропускная способность дискретного (цифрового) канала
- •3.2. Пропускная способность непрерывных (аналоговых) каналов
- •3.3. Определение пропускной способности непрерывного канала
- •3.4 Основные теоремы Шеннона
- •3.5 Энтропия источника при наличии коррелятивных связей между двумя соседними символами
- •4 Помехоустойчивое кодирование
- •Коды с обнаружением и исправлением ошибок. Код хемминга
- •Исправляющая способность кода хемминга
- •Контрольные вопросы
- •Библиографический список
- •Лабораторная работа №4 код хемминга
- •1.1. Понятие информации ...................................................................... 1
- •Контрольная работа № 1
- •Контрольная работа № 2
1.4. Свойства энтропии источника дискретных сообщений
В
соответствии с (1.6) энтропия
![]() источника дискретных сообщений
источника дискретных сообщений
![]() .
.
-
Энтропия есть величина вещественная, неотрицательная и ограниченная.
Выделим
из формулы для энтропии (1.6) одно слагаемое
![]() и докажем, что это слагаемое является
величиной вещественной, неотрицательной
и ограниченной. Заметим, что для крайних
значений
и докажем, что это слагаемое является
величиной вещественной, неотрицательной
и ограниченной. Заметим, что для крайних
значений
![]() и
и
![]() рассматриваемое
слагаемое обращается в нуль. При этом
для значения
рассматриваемое
слагаемое обращается в нуль. При этом
для значения
![]() необходимо
рассмотреть предел, который использован
в примере для двоичного канала.
необходимо
рассмотреть предел, который использован
в примере для двоичного канала.
![]() .
.
Здесь р перевели в знаменатель в виде дроби 1/р. В числителе остается –logp, который представлен как log1/p=log1– logp = –logp, т.к. log1=0.
Обозначив
![]() и воспользовавшись правилом Лопиталя,
получим
и воспользовавшись правилом Лопиталя,
получим
![]() .
.
Для
значений
![]() интересующее нас слагаемое будет
вещественным и неотрицательным. Для
доказательства ограниченности величины
интересующее нас слагаемое будет
вещественным и неотрицательным. Для
доказательства ограниченности величины
![]() найдем
найдем
![]() ,
при котором исследуемая
величина примет максимальное значение.
Для этого, как известно, надо отыскать
производную и приравнять ее нулю:
,
при котором исследуемая
величина примет максимальное значение.
Для этого, как известно, надо отыскать
производную и приравнять ее нулю:
![]() ,
,
Решая
приведенное выше уравнение, получаем .
.
Этому
значению
будет соответствовать максимальное
значение слагаемого –p(xi)log(p(xi)),
равное 0,531. Таким образом, интересующее
нас слагаемое
![]() является вещественным, неотрицательным
и ограниченным. График зависимости
величины этого слагаемого от
является вещественным, неотрицательным
и ограниченным. График зависимости
величины этого слагаемого от
![]() приведен на рис..1.2.
Поскольку энтропия представляет собой
ограниченную сумму слагаемых,
то свойства
для одного слагаемого в данном случае
можно перенести на всю сумму.
приведен на рис..1.2.
Поскольку энтропия представляет собой
ограниченную сумму слагаемых,
то свойства
для одного слагаемого в данном случае
можно перенести на всю сумму.

-
Энтропия
 лишь
в том случае, когда все вероятности
лишь
в том случае, когда все вероятности
 ,
кроме одной, равны нулю, а эта единственная
вероятность равна единице.
Следовательно,
,
кроме одной, равны нулю, а эта единственная
вероятность равна единице.
Следовательно,
 только в
случае полной определенности исхода
опыта, а в остальных случаях
только в
случае полной определенности исхода
опыта, а в остальных случаях
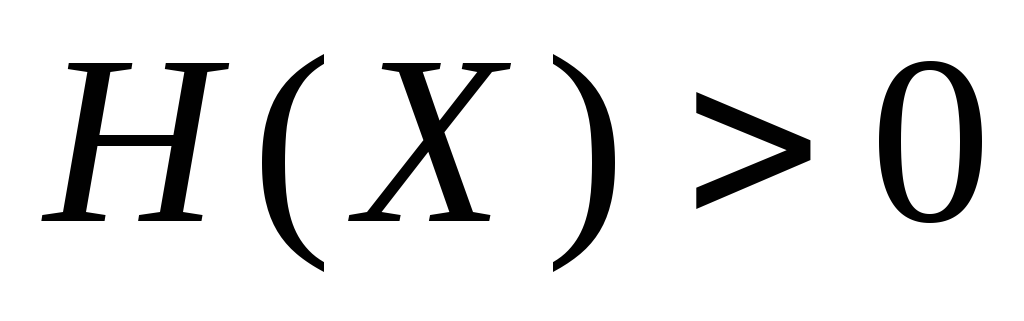 .
Последнее
вытекает из того, что
.
Последнее
вытекает из того, что
 и, как было
доказано в п.1.4.1,
и, как было
доказано в п.1.4.1,
 .
. -
При заданном
 энтропия максимальна и равна
энтропия максимальна и равна
 лишь тогда, когда все события
равновероятны,
т.е.
лишь тогда, когда все события
равновероятны,
т.е.
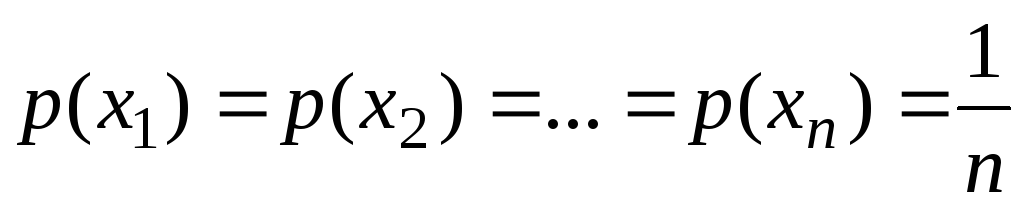 .
.
Это
свойство можно доказать следующим
образом. Для краткости записи обозначим
![]() и
представим (1.6) в виде
и
представим (1.6) в виде
![]() . (1.8)
. (1.8)
Поскольку все события xi независимы и несовместны, то сумма их вероятностей равна 1. Тогда применительно к (1.8) должно выполняться условие
![]() . (1.9)
. (1.9)
Найдем
значения
![]() ,
при которых энтропия
,
при которых энтропия
![]() имеет максимальное значение.
имеет максимальное значение.
Согласно правилу отыскания относительного максимума функции нескольких переменных с учетом (1.8) и (1.9) имеем
 ,
,
где
![]() – множитель Лагранжа.
– множитель Лагранжа.
Подставляем
в последнее равенство значения
![]() из
(1.8)
и, выполнив дифференцирование, получаем
из
(1.8)
и, выполнив дифференцирование, получаем
![]() ,
,
откуда
![]() ,
(1.10)
,
(1.10)
где
![]() .
.
Заметим,
что с учетом (1.10)
![]() ,
откуда
следует
,
откуда
следует![]() ,
что соответствует равной вероятности
событий. Найденное экстремальное
значение
,
что соответствует равной вероятности
событий. Найденное экстремальное
значение
![]() соответствует максимуму энтропии.
Изложенное свойство энтропии 1.4.3
полностью согласуется с графиком
зависимости
соответствует максимуму энтропии.
Изложенное свойство энтропии 1.4.3
полностью согласуется с графиком
зависимости
![]() от
от
![]() на рис. 1.1 для двоичного канала как
источника информации.
на рис. 1.1 для двоичного канала как
источника информации.
1.5. Энтропия источника совместных сообщений
Возьмем
два ансамбля событий:
![]() ,
который представляется (1.4)
,
который представляется (1.4)
 ,
и
,
и
![]() ,
описываемый как
,
описываемый как
 .
(1.11)
.
(1.11)
Будем
рассматривать совместные (происходящие
вместе) события
![]() и
и
![]() .
Все возможные пары
.
Все возможные пары
![]() могут рассматриваться как элементы
нового объединенного ансамбля
могут рассматриваться как элементы
нового объединенного ансамбля
![]() .
В качестве примера совместных событий
.
В качестве примера совместных событий
![]() и
и
![]() можно отметить состояния
можно отметить состояния
![]() и
и
![]() ,
формируемые в r-
и s-разрядных
регистрах, широко используемых в
информационных системах. При этом число
состояний r-разрядного
регистра составит
,
формируемые в r-
и s-разрядных
регистрах, широко используемых в
информационных системах. При этом число
состояний r-разрядного
регистра составит
![]() ,
а s-разрядного
–
,
а s-разрядного
–
![]() .
Каждому из состояний регистров с помощью
логических дешифраторов можно привести
в соответствие двоичные сигналы (события)
.
Каждому из состояний регистров с помощью
логических дешифраторов можно привести
в соответствие двоичные сигналы (события)
![]() (
(![]() )
и
)
и
![]() (
(![]() ).
Все возможные пары
).
Все возможные пары
![]() и
и
![]() могут быть реализованы с использованием
двухвходовых логических элементов «И»
(конъюнкторов). Таким образом, на выходах
этих логических элементов получим
могут быть реализованы с использованием
двухвходовых логических элементов «И»
(конъюнкторов). Таким образом, на выходах
этих логических элементов получим
![]() двоичных сигналов (сообщений), которые
можно рассматривать как элементы нового
ансамбля
двоичных сигналов (сообщений), которые
можно рассматривать как элементы нового
ансамбля
![]() .
.
Объединенный ансамбль таких сообщений представим в виде
-




…





…

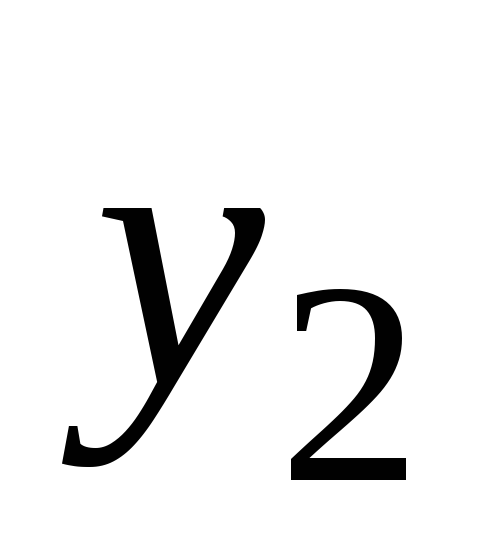


…









…

Ансамбль
![]() может рассматриваться как некий новый,
в котором возможны
может рассматриваться как некий новый,
в котором возможны
![]() различных состояний (событий)
различных состояний (событий)
![]() с заданным распределением вероятностей
с заданным распределением вероятностей
![]() .
.
Энтропия
такого ансамбля, т.е. энтропия исхода
совместных событий
![]() ,
может быть получена по аналогии с
энтропией
,
может быть получена по аналогии с
энтропией
![]() (1.8) в следующем виде:
(1.8) в следующем виде:
![]() .
(1.12)
.
(1.12)
Известно, что вероятность совместного события равна произведению вероятности одного события на условную вероятность другого события, при условии, что произошло первое событие [3]
![]() ,
(1.13)
,
(1.13)
где
![]() – вероятность события
– вероятность события
![]() при условии, что произошло событие
при условии, что произошло событие
![]() (условная вероятность
(условная вероятность
![]() ),
),
![]() – условная вероятность
– условная вероятность
![]() .
.
Проделав подстановку (1.13) в (1.12) и соответствующие преобразования, получим
 .
(1.14)
.
(1.14)
Для
условных вероятностей известно, что
![]() [3],
тогда выражение (1.14) с учетом (1.8) можно
привести к виду
[3],
тогда выражение (1.14) с учетом (1.8) можно
привести к виду
![]() ,
(1.15)
,
(1.15)
где
![]() .
(1.16)
.
(1.16)
Здесь
![]() будем называть условной энтропией
ансамбля
будем называть условной энтропией
ансамбля
![]() .
Условную энтропию структурно можно
рассматривать как математическое
ожидание частных условных энтропий
.
Условную энтропию структурно можно
рассматривать как математическое
ожидание частных условных энтропий
![]() ансамбля
ансамбля
![]() .
Следовательно, условная энтропия
.
Следовательно, условная энтропия
![]() равна среднему значению частных условных
энтропий и характеризует неопределенность
исхода событий
равна среднему значению частных условных
энтропий и характеризует неопределенность
исхода событий
![]() при известных событиях
при известных событиях
![]() :
:
 .
.
Легко
видеть, что условная энтропия
![]() ,
так же как энтропии
,
так же как энтропии
![]() и
и
![]() ,
– величина положительная, т.е.
,
– величина положительная, т.е.
![]() .
.
Обратим внимание на то, что формула (1.13) для вероятности совместных событий, по сути, имеет две формы записи. Используя это, нетрудно представить и энтропию совместных событий в двух видах:
![]() .
(1.17)
.
(1.17)
