
KMSF-Chast2-new
.pdf
Объем шарового слоя равен
d E
d шар
4 p |
2 |
dp |
|
.
Учитывая, что
p
|
2mE |
,
запишем
d E
d шар dE 4 p 2 dE
dp |
dE |
|
dE |
||
|
. Итак, вероятность для молекулы идеаль-
ного газа иметь энергию в интервале от E до E + dE равна
dP E 4 m |
3 / 2 |
2E E dE |
E dE |
|
|
|
|
|
|
E |
|
(1.42)
Функция распределения молекул по
ся соотношением |
E E 4 m |
3 / 2 |
E |
|
|
|
их энергиям, следовательно, определяет-
2E .
Важно отличать друг от друга две функции распределения. Функция микрораспределения E E q, p представляет собой плотность вероятности обнаружить систему в единице фазового объема с координатами q и p.
Функция макрораспределения E E представляет собой плотность вероятности обнаружить систему в состоянии с определенной энергией при всех координатах и импульсах, соответствующих этой энергии (шаровой слой в фазовом пространстве).
Зависимость |
E |
от энергии. Используя вероятностные соображения, |
можно найти зависимость функции E от энергии. Выделим в газе квазиза-
мкнутую подсистему из двух невзаимодействующих молекул. Энергия под- |
||
системыаддитивная величина - |
E E1 E2 . Функция распределения подси- |
|
стемы по теореме умножения |
вероятностей равна |
E E1 E2 . |
Таким образом, функция распределения не аддитивная величина. Так как всегда удобнее работать с аддитивными величинами, то будем в квазизамкнутой системе рассматривать логарифм распределения, который есть аддитивная величина от энергии:
ln E ln E1 ln E2 . |
(1.43) |
Выражение (1.43) выполняется только тогда, когда ln E является линейной функцией энергии E
ln ( E ) E , |
(1.44) |
где и неизвестные пока постоянные. Итак, в общем случае
E
const e |
E |
|
.
(1.45)
До сих пор рассматривали идеальный газ. Однако все эти рассуждения могут быть применены к произвольному макроскопическому телу (неидеальные газы, жидкость, твердое тело). Для этого надо выразить дифференциал d E через дифференциал dE и ввести функцию макрораспределения подсистемы по энергиям:
21

d |
|
|
|
E |
|
|
|||
|
|
|
|
|
|
E |
|
E |
|
|
|
|
|
|
§1.8.Энтропия.
dE
,
dP E E |
|
|
E |
||
|
||
|
E |
dE
|
E |
|
E dE
,
E E E E
E
.
Флуктуации аддитивных величин. Итак, нам известно, что статистическое поведение и свойства замкнутой (квазизамкнутой) системы определяются
аддитивными интегралами движения. Одним из наиболее важных свойств аддитивных величин является то, что их флуктуации в состоянии равновесия
малы (
~ |
1 |
|
N |
||
|
, где N число подсистем). Для доказательства разобьем квазиза-
мкнутую подсистему на множество более мелких, квазизамкнутых одинаковых подсистем (каждая из них слабо взаимодействует с окружением). Пусть число таких подсистем N. Тогда энергия подсистемы равна сумме энергий
более мелких подсистем:
E
N
i
i1
. Для оценки средней энергии подсистемы
можно считать, что средние энергии малых подсистем одинаковы, поскольку мы разбивали на мелкие одинаковые подсистемы. Тогда средняя энергия равна  E
E N
N 
 . Сосчитаем среднюю квадратичную флуктуацию
. Сосчитаем среднюю квадратичную флуктуацию
2 |
E |
2 |
|
|
N |
2 |
E |
E |
|
i |
|||
|
|
|
|
|
i 1 |
|
N
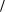 i 2
i 2 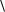 (1.46)
(1.46)
i 1
При выводе этой формулы мы воспользовались тем, что
|
i |
|
0
. То, что
формула справедлива, проще всего увидеть на примере двух малых подси-
стем |
|
с |
энергиями |
1 и |
2. |
|
В |
самом |
деле, |
для |
двух подсистем |
|||||||||
E |
|
|
1 |
|
2 1 |
2 2 |
|
|
|
1 |
|
|
|
2 |
|
|
2 1 2 |
. В силу квазине- |
||
|
2 |
|
|
2 |
|
|
2 |
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
зависимости малых подсистем |
|
1 |
2 |
|
1 |
|
2 0 |
, т.к. |
i 0 . Поэтому |
|||||||||||
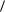 E 2
E 2 
 1 2
1 2 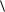
 2 2
2 2  . Аналогичный результат получается и для N малых
. Аналогичный результат получается и для N малых
подсистем. Воспользуемся еще раз тем, что малые подсистемы примерно одинаковы, и флуктуации в них в среднем также имеют одинаковые величины
E |
2 |
N |
|
2 |
. |
(1.47) |
|
|
|
|
|
Тогда для относительной квадратичной флуктуации получаем:
E 2 |
N 2 |
|
1 |
2 |
|
|
|
|
|
(1.48). |
|
N |
|
|
|||
E |
|
N |
|
Как видно из этого соотношения, при больших значениях N относительные флуктуации ничтожно малы. Как и для распределения молекул по объему
22
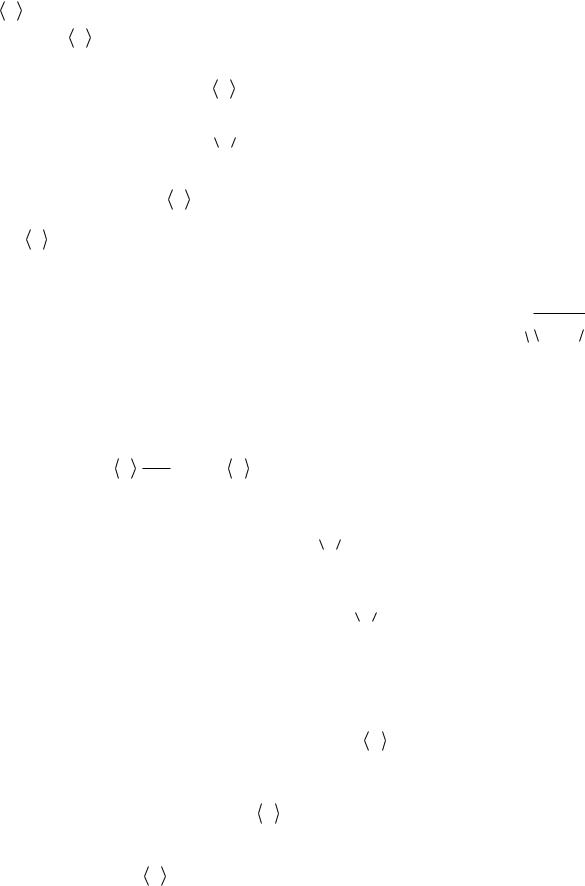
квазизамкнутая система живет подавляющую часть времени в состоянии с энергией близкой к средней энергии. Иначе, энергия равновесной подсистемы E практически постоянна во времени и равна своему среднему значению:
E E . Это означает, что функция распределения имеет резкий пик при |
|
энергии E E и имеет качественную зависимость, изображенную на рисун- |
|
ке. Заметную величину E E |
имеет только при ничтожно малых отклонени- |
ях E от среднего значения E |
E . Итак, любая квазизамкнутая система почти |
все время проводит в очень небольшой части фазового пространства, соответствующей энергии вблизи  E
E  . Эту область можно оценить, исходя из то-
. Эту область можно оценить, исходя из то-
го, что площадь под кривой равна единице : |
|
|
E E E 1 , |
|
(1.49) |
где E E высота области, а E ширина этой области (на полувысоте). |
||
Статистический вес. По порядку величины |
E |
(т.е. тот интервал энергий, в |
котором допустимы малые отклонения энергии подсистемы от своего сред-
него значения) совпадает со средней квадратичной флуктуацией

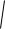
 E 2
E 2 
.
Поэтому для оценки разрешенной части фазового пространства, в которой рассматриваемая подсистема проводит подавляющую часть времени, можно в распределении по энергиям поставить среднее значение энергии. Тогда (1.49) можно записать в виде
E |
d |
E E |
1. |
|
E |
||||
|
|
|
||
|
dE |
E |
|
|
|
|
|
(1.50)
Здесь |
|
E |
- та разрешенная часть фазового пространства, в которой рассмат- |
|
риваемая подсистема со средней энергией  E
E  проводит подавляющую часть
проводит подавляющую часть
времени. Объем
|
E |
|
несет информацию о полном числе микроскопиче-
ских состояний подсистемы, которые реализуют макроскопическое состояние равновесной подсистемы с энергией  E
E  .
.
Введем понятие статистического веса как числа микросостояний реализую-
щих данное макросостояние. При статистическом описании |
тепловых |
|
свойств тел роль статистического веса играет фазовый объем |
|
E . Этот |
|
||
объем тем больше, чем больше число микроскопических реализаций макро-
скопического состояния подсистемы с энергией |
E |
. Однако, статистический |
вес, как он вводится по определению, есть величина безразмерная, а фазовый |
|||
объем E - размерная величина. Поэтому определим статистический вес |
|||
макроскопического состояния |
E |
как |
величину, пропорциональную |
фазовому объему E : |
|
|
|
E E |
|
|
(1.51) |
|
23 |
|
|

где - размерный коэффициент пропорциональности. |
||
Если подсистему со средней энергией |
E |
разбить на подсистемы меньшего |
размера, то состояние каждой малой подсистемы будет определяться ее
средней энергией. Для каждой маленькой подсистемы можно определить |
||
статистический вес i i ее макросостояния с энергией в интервале от |
i |
|
до |
i i . Так как маленькие подсистемы статистически независимы, |
то |
энергия рассматриваемой подсистемы  E
E
 i
i  , а её статистический вес
, а её статистический вес
i
по теореме об умножении вероятностей равен
E |
|
1 |
|
|
2 |
... |
|
|
i |
... |
1 |
|
2 |
|
|
i |
|
|
(1.52)
Энтропия. Удобнее вводить аддитивную величину, характеризующую макроскопическое состояние подсистемы (аддитивные величины обладают малыми флуктуациями). Энтропия подсистемы определяется соотношением
S  E
E ln
ln  E
E .
.
Энтропия дает информацию, как и
росостояний подсистемы, |
которые |
|
системы с энергией |
E . |
Термин |
(1.53)
статистический вес, о полном числе микреализуют данное равновесное состояние энтропия на греческом языке означает
“превращение”. Число микроскопических реализаций растет с увеличением степени беспорядка в подсистеме. Поэтому говорят, что энтропия является мерой степени беспорядка в подсистеме.
Из (1.51) получаем
S  E
E ln E .
ln E .
(1.54)
Энтропия большой подсистемы, статистический вес которой равен произведению статистических весов малых подсистем
E 1 1 |
2 2 |
... |
, |
равна сумме энтропий её малых равновесных частей
S E S1 1 |
S2 2 |
... |
(1.55) |
Энтропия - аддитивная величина. Следовательно, для энтропии флуктуации
также малы
~
1 |
|
N |
1/ 2 |
|
|
. Из свойства аддитивности следует, что энтропия помимо
энергии зависит от объема тела V, но не зависит от формы тела, т.к. изменение формы тела - это только перестановка его частей, соответствующая перестановке слагаемых в сумме энтропий отдельных малых подсистем. Таким образом, энтропия S S E,V , т.е. макроскопическое состояние определяется всего двумя параметрами: энергией тела E и его объемом V. Небольшое из-
24

менение макроскопического состояния тела сопровождается малым изменением энтропии dS, которое состоит из двух вкладов
|
S |
|
|
S |
dV |
dS |
|
|
dE |
|
|
|
|
|
|
|
|
|
E |
V |
|
V |
E |
|
|
|
|
.
(1.56)
Здесь первое слагаемое - приращение энтропии за счет изменения энергии тела, второе - за счет изменения объема тела.Во всех имеющихся в природе замкнутых системах энтропия никогда самопроизвольно не убывает, она уве-
личивается или остается постоянной
dS dt
0
. Закон возрастания энтропии
устанавливает определенное направление течения процессов в природе.
Глава 2. Распределение Гиббса.
§2.1. Канонический ансамбль. Распределение Гиббса.
Канонический ансамбль – это совокупность незамкнутых систем. Каждая из этих систем является частью большой замкнутой системы.
Найдем функцию распределения систем канонического ансамбля по энергиям
|
|
E E |
d |
|
E |
||
|
|
|
|
|
E |
|
dE |
|
|
|
.
(2.1)
Эта функция была введена для некоторого макроскопического равновесного тела (подсистемы), помещенного в окружающую среду (резервуар) и составляющего с этой средой замкнутую систему. Взаимодействие такого тела с окружающей средой слабое и в полном балансе энергий им можно пренебречь. Полная энергия замкнутой системы равна
E0 E E const , |
(2.2) |
где E - энергия тела (подсистемы), E' - энергия резервуара.
Е'
Е
Рис.2.1. Замкнутая система, состоящая из маленькой подсистемы и резервуара.
25
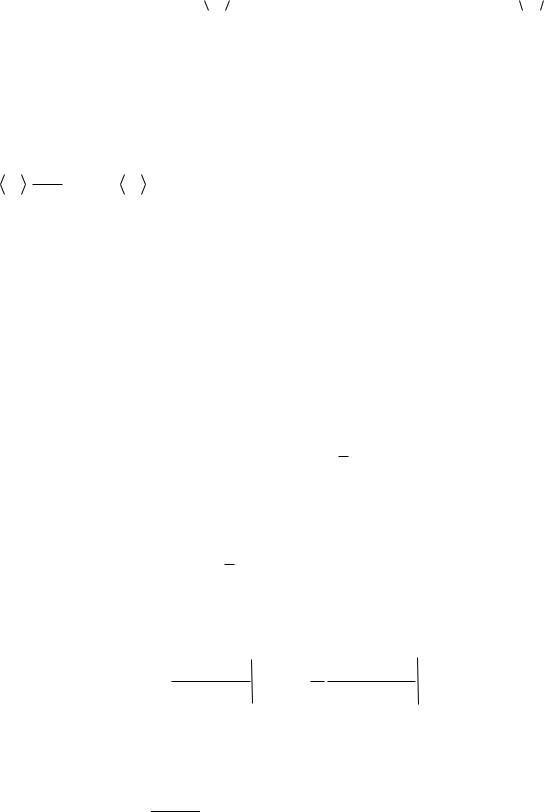
Пусть размер подсистемы (тела) значительно меньше размера системы, т.е. E' >> E. Для числа частиц в полной системе и подсистеме имеет место условие N 0 N N' N . Так как в макроскопических телах флуктуации энергии в состоянии равновесия малы, то можно считать, что энергия среды E' есть среднее значение энергии  E
E  . В дальнейшем знак усреднения
. В дальнейшем знак усреднения  E
E  писать
писать
больше не будем, всегда подразумевая средние значения энергии для больших систем в равновесии.
Нас интересует вероятность |
dP E такого состояния подсистемы, в кото- |
ром тело находится в состоянии с энергией от E до E + dE, а окружающая среда - в равновесном макроскопическом состоянии со средней энергией E'. Это состояние среды можно описать фазовым объемом E . Напомним, что
E |
|
|
d |
E |
|
E |
|
E 1, |
|
|
|
|
|
||
E' |
а |
статистический вес состояния равен |
|||||||||||||
dE |
|||||||||||||||
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
a E . |
Фазовый объем |
E пропорционален числу способов распре- |
||||||||||
E |
|||||||||||||||
деления энергии E E0 E |
по окружающей среде. Так как тело и среда ста- |
||||||||||||||
тистически независимы, то вероятность |
|
dP E пропорциональна произведе- |
|||||||||||||
нию фазового объема состояния тела |
d |
E |
и фазового объема макроскопиче- |
||||||||||||
|
|||||||||||||||
ского состояния окружающей среды E
dP E ~ |
d |
E' |
E |
.
(2.3)
Фазовый объем макроскопического энтропию окружающей среды - S' E'
S ' E |
0 |
E ln a |
E ' |
|
|
состояния среды можно выразить через |
|||||||
ln E' ln a E' . |
|||||||
|
|
|
1 |
exp S ' E |
|
E . |
|
E ' |
a |
0 |
|||||
|
|
|
|
||||
|
|
|
|
|
|
||
Подставляя последнее выражение в (2.3), получаем:
dP E ~ |
1 |
e |
S' E |
E |
d |
|
|
|
0 |
|
|
|
a |
|
|
|
E |
|
|
|
|
|
Учтем, что тело составляет малую часть системы, т.е. тропию среды S'(E0-E) в ряд в окрестности точки E0:
(2.4)
Е << E0. Разложим эн-
S' E |
|
E S' E |
|
|
dS' E |
|
E |
|
|
1 d |
2 |
S' E |
|
E |
|
|
|
|||||
|
|
0 |
E |
|
0 |
E |
2 |
... |
||||||||||||||
|
0 |
|
0 |
|
d E |
|
|
E |
|
|
2! |
d |
E |
|
E |
2 |
|
|
|
|||
|
|
|
|
|
0 |
|
|
E 0 |
0 |
|
E 0 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
и ограничимся первым порядком в разложении по энергии Е.
Обозначив
′(0) = = 1/,
0
(2.5)
(2.6)
26

где k- постоянная Больцмана, T- абсолютная температура, получаем
dP E Aexp E d E .
(2.7)
Здесь Е - энергия изучаемого тела, зависящая от координат и скоростей составляющих его атомов или молекул. Постоянную А можно найти из условия
нормировки ∫0 0 ( ) = 1. Из (2.7) получаем
A |
|
1 |
|
E |
|
|
|
exp E d |
(2.8)
Сравнивая выражение (2.7) с
dP E |
|
E dE E |
d |
|
E |
||
|
|
|
|
|
E |
|
dE |
|
|
|
dE
E d E
,получаем
плотность вероятности - функцию статистического распределения
E A e |
E |
|
(2.9)
Это и есть распределение Гиббса. Формула (2.9) дает распределение вероятностей различных микроскопических состояний подсистемы, являющейся малой частью некоторой большой замкнутой системы.
§2.2. Распределение Максвелла и его свойства.
В классической физике полная энергия всегда может быть разделена на кинетическую K и потенциальную U энергии
E E |
k |
|
E |
p |
|
K U
,
(2.10)
где K - функция скоростей, U - функция координат. Функция U, вообще говоря, состоит из потенциальной энергии взаимодействия атомов между собой и из потенциальной энергии во внешнем поле. При этом элемент фазового объема можно представить в виде произведения двух элементов
|
d d |
p |
|
|
|
где d K |
d p элемент фазового |
|
d |
(2.11) |
q , |
объема в пространстве импульсов (скоро-
стей), d U d q фазовый объем в пространстве координат. Тогда вероятность записывается
d P E d P K d P U |
(2.12) |
Такое разбиение вероятности
d P E
на два независимых сомножителя озна-
чает, что вероятность иметь определенные значения для кинетической энергии никак не влияет на вероятность иметь какие-то значения для потенциальной энергии. Поэтому вероятности d P K и d P U должны удовлетворять независимым условиям нормировки для определения постоянных a и b:
27

dP K dP U
|
|
K |
|
|
, |
a exp |
d |
p |
|||
|
|
kT |
|
|
|
|
|
|
|
||
|
|
U |
|
|
|
b exp |
d . |
||||
|
|
kT |
q |
|
|
|
|
|
|
||
(2.13)
Такое разбиение распределения по полным энергиям на два независимых распределения по кинетическим и потенциальным энергиям возможно лишь в классической физике. При квантовом рассмотрении вероятности различных значений координат и импульсов оказываются связанными друг с другом за счет соотношения неопределенностей.
Распределение Максвелла по абсолютным значениям скорости.
Разбиение вероятности
d P
на произведение вероятностей
d P |
d P |
K |
U |
позволяет
найти распределение молекул газа по абсолютным значениям скоростей. Пусть система состоит из большого числа невзаимодействующих молекул.
Кинетическая энергия системы
K K |
1 |
K |
2 |
... K |
i |
|
|
|
...
, где
|
|
|
p |
2 |
|
mv |
K |
|
|
i |
|
||
|
|
|
|
|
|
|
|
i |
|
2m |
|
2 |
|
|
|
|
|
|||
2 i
-
кинетическая энергия молекулы. Соответствующий фазовый объем равен
d p d p |
d p |
d p |
... Поскольку все частицы одинаковы и каждую из них |
|||||||||||||||||
1 |
|
|
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
можно рассматривать, |
как независимую подсистему, то вероятность имеет |
|||||||||||||||||||
вид произведения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
K |
i |
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
i |
|
|
|
|
K |
i |
|
|
K |
|
d PK |
|
|
||||
|
|
|
|
|
a e |
|
|
|
|
|
|
1 |
|
|
|
|
||||
d PK a e |
|
|
|
d p |
|
|
|
d p |
|
a e |
|
|
d p |
|
N |
(2.14) |
||||
|
kT |
|
kT |
|
kT |
, |
||||||||||||||
|
|
|
|
|
|
i |
|
|
|
|
i |
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где
d P |
|
K |
1 |
- пропорциональна распределению вероятностей по абсолютным
значениям скоростей каждой отдельной молекулы:
|
|
|
|
|
|
mv |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
dP |
|
A exp |
|
1 |
d |
|
|||
1 |
|
|
1 |
||||||
K |
|
|
|
|
|
|
|
||
|
|
|
|
|
2kT |
p |
|||
|
|
|
|
|
|
||||
|
|
A |
N |
a, |
|
|
|
||
|
|
|
|
|
|
||||
(2.15)
Элемент объема
d |
p |
|
1 |
dp |
dp |
dp |
1x |
1y |
1z |
. Итак, функция распределения вероятно-
стей по кинетическим энергиям для одной молекулы имеет вид
|
|
mv |
2 |
|
K |
Aexp |
1 |
. |
|
|
|
|
||
1 |
|
|
||
|
|
2kT |
||
Вероятность молекулы иметь кинетическую энергию от K1 до K1 дая при этом определенными проекциями импульсов, равна
|
|
|
|
p 2 |
|
|
|
|
|
|
dP |
px , p y , pz |
A exp |
|
|
dp |
dp |
y |
dp |
z |
|
|
||||||||||
|
|
|
2m |
|
x |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
(2.16)
+ dK1, обла-
(2.17)
28
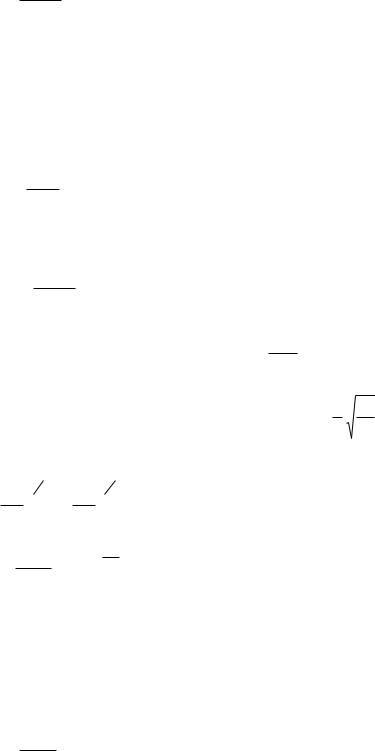
Аналогично, вероятность молекулы иметь кинетическую энергию от K1 до K1 + dK1, обладая при этом определенными проекциями скорости, равна
|
|
|
mv |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dP |
Aexp |
|
|
|
dv |
dv |
dv |
z |
|
vx ,vy ,vz |
|
|
2 |
|
|
x |
y |
|
|
|
|
|
|
|
|
|
|
|
|
(2.18)
Фазовый объем, соответствующий кинетической энергии, лежащей в диапазоне от K1 до K1 + dK1 при всех возможных импульсах или скоростях, опре-
деляется шаровым слоем |
d K 4 p |
|
dp |
или |
d K |
4 v |
dv . Вероятность иметь |
|
|
2 |
|
|
|
2 |
|
кинетическую энергию от K1 до K1 + dK1 |
при всех возможных импульсах |
||||||
равна |
|
|
|
|
|
|
|
|
|
|
p |
2 |
|
|
|
|
|
|
|
|
|
|
|
dP |
A exp |
|
|
|
4 p |
2 |
dp |
|
|
|
|||||
K |
|
|
2m |
|
|
|
|
|
|
|
|
|
|
||
В пространстве скоростей
(2.19)
|
|
|
mv |
2 |
|
|
|
|
|
|
|
|
|
|
|
dP |
A exp |
|
|
|
4 v |
2 |
dv |
|
|
|
|||||
K |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
Постоянную А найдем из условия нормировки
|
K |
|
dP |
|
|
|
|
4 A |
|
||
|
|||
|
exp |
||
|
0 |
|
mv |
2 |
|
|
2kT |
|
v 2 dv
(2.20)
1.
Пользуясь табличным интегралом Пуассона -
|
|
|
|
|
1 |
|
||
exp x |
2 |
x |
2 |
dx |
||||
|
|
|
||||||
|
|
4 |
|
3 |
||||
0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
,
получаем:
|
m |
3 |
|
m |
3 |
2 |
2 |
||||
A |
|
|
|
|
|
|
2 |
|
|
2 |
|
,
(2.21)
|
|
|
|
3 / 2 |
|
mv |
2 |
|
|
|
|
m |
|
|
|
2 |
|
||||
|
|
|
|
|
|
|||||
dP |
|
|
|
e |
2kT |
4 v |
|
dv |
||
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||
v v dv |
|
2 kT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
.
(2.22)
Формула (2.22) дает вероятность того, что скорость молекулы лежит в диапазоне от v до v + dv, т.е. в шаровом слое пространства скоростей.
Свойства распределения Максвелла:
1) Плотность вероятности
f(v)
dP v dv
, имеет максимум при некоторой скоро-
сти v молекул. Из (2.22) следует, что при малых скоростях вероятность растет пропорционально v2 из-за фазового объема, а далее с ростом скорости v функция резко убывает из-за экспоненциального множителя. Найдем наиболее вероятную скорость, т.е. скорость, при которой имеется максимум функ-
29
|
|
|
|
|
|
f v ~ v |
|
|
|
|
|
mv |
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ции f(v). Так как |
|
2 |
|
|
|
|
|
|
|||||||||
|
|
exp |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2kT |
|||
|
|
|
|
|
mv |
2 |
|
|
|
|
|
mv |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
получаем |
|
v |
|
e |
|
|
0 2ve |
|
|
|
m |
||||||
|
2 |
2kT |
|
2kT |
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kT |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(v) f(v)
, то, приравнивая нулю её производную,
|
|
|
mv |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2kT |
|
|
v |
3 |
2kT |
v |
|
|
. |
|||
e |
|
|
|||||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
вер |
|
m |
|
|
|
|
|
|
|
|
|
|
|
vвер |
v v+dv |
v |
Рис.2.2. Распределение Максвелла по абсолютным значениям скорости.
Максимум получается при скорости, которая и называется
ной скоростью
vвер |
2kT |
; |
|
m |
|||
|
|
наиболее вероят-
(2.23)
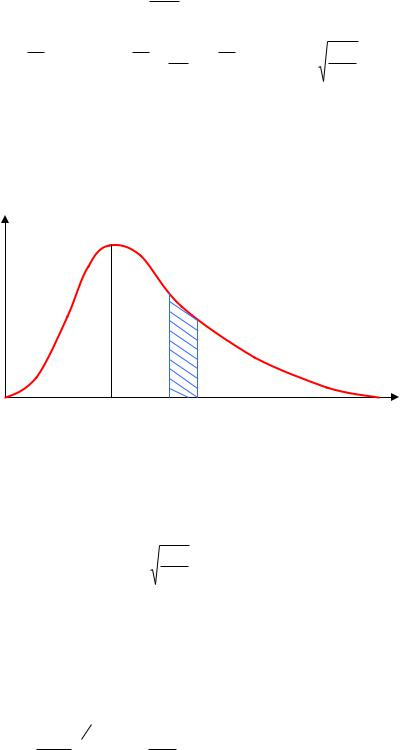
2) Полная площадь под кривой f(v) равна 1, поскольку она равна нормировочному интегралу. Интерпретация участка заштрихованной площади под кривой: площадь заштрихованной области равна вероятности того, что скорость молекулы в диапазоне от v до v + dv. Для вероятности получить скорость молекул в конечном интервале скоростей необходимо вычислить
|
|
|
|
v |
2 |
|
|
m |
|
3 |
2 |
v |
2 |
|
mv |
2 |
|
|
|
|
|
|
|
f v dv |
|
|
|
||||||||||||
|
|
|
|
|
|
|
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
2 |
|
|
|
|
|
|
|
|
dv |
||||||||
P |
v |
|
|
|
|
|
|
|
|
|
|
exp |
|
|
4 v |
|
|||
v |
|
|
|
|
|
|
|
|
|
|
|
2kT |
|
|
|||||
|
|
|
|
v |
|
|
2 kT |
|
|
v |
|
|
|||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
;
(2.24)
3) Распределение вероятностей зависит от температуры. На рисунке 2.3 представлено несколько кривых f(v) при разных температурах.
30
