KMSF-Chast2-new

Средняя энергия одной частицы равна

= −

ln =

3

=

3

,

а сред-

2

2

няя энергия всех частиц =

3

.

Используя полученные выражения для

2

Z, можно найти среднее давление . Для этого примем во внимание, что

= −

,

= −

.

Тогда

1

1

1 ln

1 ln

1

=

∑ (−

) −

=

=

=

=

.

Отсюда получаем, что

=

=

=

= .

§3.2. Идеальный газ Бозе - Эйнштейна.

Рассмотрим систему невзаимодействующих бозонов, находящихся в объеме V . В соответствии с (3.1) запишем статистическую сумму в явном виде

		≡	−		=	∑	−{1(1− )+ ( − )+ … }		=
						1,2,..
∑	1	−[1(1− )] ∑		2	−[2(2− )] …			( =0,1,2,3, ….)	(3.13)

Каждый из сомножителей (бесконечных рядов) в этом выражении равен

∑

−[ ( − )]

2

1

1

= (1 + +

+ ≡ ) =

1−

− ( − ) .

(3.14)

1−

Для статсуммы и свободной энергии имеем:

	−	= ∏					1			,				=		1	∑ ln[1 −	− ( − )	],	(3.15)
					1−− ( − )
						=			=				1		.					(3.16)
												(	− )
														−1

Последнее выражение называется функцией распределения Бозе-Эйнштейна, которая описывает распределение бозонов по энергиям.

Если учесть спин, то надо умножить свободную энергию на число спиновых состояний s . Сумму (3.15) можно найти, если заменить её интегралом по

41

																																																																									2
фазовому объёму и заменить дискретный спектр непрерывным																																																																=		=
2 2																																																																									2
			. Заметим, что теперь индекс можно заменить индексом p																																																																или k . То-
	2
гда, с учетом (3.10),
																																2
						=							∫ ln (1 − −																							)										3									∫ 3 ,
																														2																																										(3.17)
																																													(2 )3
																																										−			2
																						1																							2																		3
						=												= −										=								∫																																	.			(3.18)
																																														2														(2 )3
																																						1−− 2
Введем обозначения:																		= ,																		2 =								2			.						Тогда
																																												2
	3				42				2										2	3/2
				=		=									(					)						,						и
	(2 )3				(2 )3			22 3
																									−2																			2																					3
																																																							2										2
									= ∫																												[														(												) ] =
																					1 −									−2												2				2 3
								3															2								3																																		3
														2																																																					2			3	( )
					= (22) ( + 3 +																										3 + ) = (22)																																									(3.19)
																																																																						2
																					22									32
																																	( ) ≡ ∑∞																																	. Задав , можно найти ,
Мы ввели здесь								дзета-функцию
																																																			=1
а затем и .
Для полной энергии (3.12) получаем
																																														3
									( )													̂											3																	2
					=													+ =																					(										)				5/2( ) .																			(3.20)
																																				2							2 2
Рассмотрим случай малых плотностей или высоких температур, когда
		1			1 1																															3( ) = , 5( ) = . В этом классиче-
3/2
																																				2																									2
																																		3 25( )																			3
ском предельном случае																														≈																		=										.
																																				2						3( )											2
																																										2

Конденсация Бозе - Эйнштейна.

Особый интерес представляет собой случай низких температур. При понижении температуры параметр неограниченно возрастает, а дзета-функция

42

при > 1 расходится. Температура, при которой = 1 называется критической температурой Tc конденсации Бозе - Эйнштейна. Известно, что

3(1) = 2.612 , 5(1) = 1.341, и из (3.19) находим

2	2
	=	22	(	/	)2/3.	(3.21)
			2.612

Вблизи этой температуры заменять суммирование (3.15) интегрированием нельзя, так как низшие дискретны уровни вносят заметный вклад в сумму.

Рассмотрим =		1							. Так как																		> 0, то должно выполняться
		( − )					−1
условие ( − ) > 0.
Пусть 0- основное невырожденное состояние, тогда
1		=					1																	0 =													1							.
						(			− )			−1																				(					0		− )
							1																																				−1
Если теперь взять 0 за начало отсчета энергии																																(т. е. принять, что 0=0), то
									0 =															1				.
																							−−1
Отсюда следует, что		= − ln(1 +																						1	),		а для больших
																						0																								0
											= −																.
																								0
При низких температурах T химический потенциал																																											должен лежать вблизи
нуля, поэтому для всех энергий													>											им можно пренебречь.
																					0
Тогда для T < Tc :
возб = − 0 = ∑=1∞																								1			∫																1				3		=
																			−1																							2					(2 )3
																																										2			−1
																	3																						3
		= 2.612 (														)		2		= (																)				2		,							(3.22)
										22
																																							3
0 = − возб = [1 − (																																			)2],														(3.23)
														3
= 0.513			3			(							)2				,										=							~ 5/2.															(3.24)
		2

43

			3		5( )
	Для T > Tc	внутренняя энергия имеет вид =			2	. Эта функция
			2		3( )
					2

убывает с ростом температуры. Вблизи критической температуры теплоёмкость имеет острый излом (“cusp”).

§3.3. Идеальный газ Ферми - Дирака.

Для идеального газа фермионов (электронов) свободная энергия также определяется формулой (3.15), в которой числа заполнения могут принимать всего два значения = 0, 1. Поэтому

= − 1 ∑ ln[1 − − ( − )],

			=		=			1			.	(3.25)
							(		− )
										−1

Последнее выражение называется функцией распределения Ферми-Дирака, которая описывает распределение фермионов по энергиям. Для вычисления свободной энергии снова перейдем от суммирования к интегрированию и учтём, что для электронов s=2:

1													− (		2		− )								3
= −2						∫ ln [1 +								2						]									∫ =
																						(2 )3
																								2
= −2											∫ ln [1 + − (													2		− )] 4 2 =
								3
			(2 )
								∫ ln [1 + − (										2		− )] 2 ,
= −																		2													(3.26)
				2 3
																			2
																− (							− )
								1											2									42
=						= −						= 2 ∫
																														.	(3.27)
																	− (				2				− )			(2 )3
															1+						2

Рассмотрим некоторые свойства функции распределения Ферми-Дирака.

44

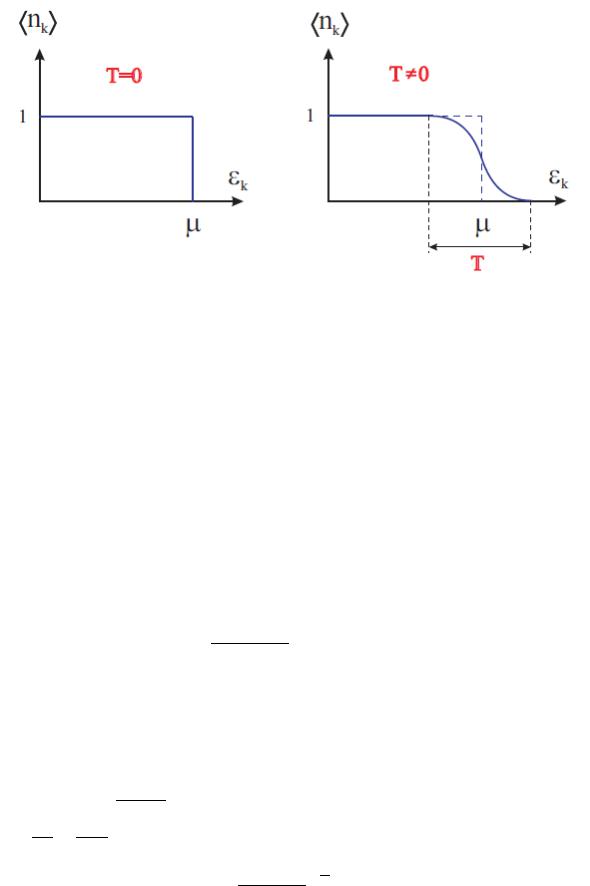
Рис.3.1. Заполнение состояний идеального ферми-газа при Т = 0 и при Т > 0.

Из (3.25) следует, что при Т = 0 все состояния с энергиями				< запол-
				0
нены, а состояния с большими энергиями	>	0	свободны.

Так как свободные электроны занимают в импульсном пространстве сферу радиуса p0, то

			42					4	3		1
= 2	∫	0		= 2			(	0		)		.	(3.28)
			(2 )3					3			(2 )3
	0
Величина
					2
			=		0								(3.29)
			0		2

называется энергией (уровнем) Ферми, а = 0/ –температурой Ферми.

Для простых металлов эту температуру можно оценить, используя две по-

следние формулы - 0 = 2(32)2/3. Оказалось, что, например, для меди (и

2

других металлов в твердом состоянии) ≈ 82000 K T. Говорят, что мы имеем сильно вырожденный электронный газ.

Найдем теперь плотность электронных состояний ( ), т.е. число состоя-

ний с энергией в интервале . Этому интервалу в импульсном пространстве отвечает сферический слой толщиной dp. Полное число состояний в

данном слое 2 42 = ( ) . Отсюда для квадратичного закона дисперсии

(2 )3

= 2 = 2 2 получаем

2 2

3/2
( )= 4 (2 )(2 )3	√ .	(3.30)

Полная энергия на единицу объёма при T=0 определяется выражением

45

								2			42							45
=		=	(0)	= 2	∫	0	(			)					=					0			, а средняя энергия электрона в
								2			(2 )3							5 (2 )3
					0
металле равна
									(0)			=		3 2				=	3			= .		(3.31)
																					0
														5 2					5

Для Т ≠ 0 функция распределения расплывается (см. Рис.3.1.), а плотность и внутреннюю энергию можно вычислить лишь приближенно. Энергетический интервал расплывания функции распределения порядка kT, что много меньше значения уровня Ферми 0. В результате для низких температур имеем:

								1				2
≈ 0(1 −											(					) ),
					12
													0
=	3	[1 +			5				2			(			)2 + ],
	5	0		12										0
				2													3/2
= 0 + 2		( =					√			0			2, =				4 (2 )	) .	(3.32)
																	3
		6															(2 )

Отсюда следует линейная зависимость удельной теплоемкости металлов

от температуры	=		= 2 .

§3.4. Статистический оператор (матрица плотности) и корреляционные

функции.

Известно, что в квантовой механике каждой физической величине A соответствует оператор ̂. Наблюдаемыми на опыте значениями этой величины являются квантово - механические средние

	≡	̂		≡ ∫		̂		( ),	(3.33)
		| |				( )

где ( ) – ортонормированные собственные функции гамильтониана системы:

̂		( ) =	( ).	(3.34)

В (3.34) индекс n нумерует состояния, - совокупность независимых координат, - соответствующие собственные значения. Если оператор ̂ коммутирует с гамильтонианом ̂, то система { } является системой его собственных функций, а наблюдаемые значения (3.33) будут собственными значениями оператора ̂.

В квантовой статистической механике под наблюдаемой величиной понимается её среднее статистическое значение, которое определяется выражением

46

̂				.	(3.35)
= ∑

В этом выражении - вероятность обнаружить систему в состоянии n, или статистический вес этого состояния. Очевидно, что должно выполняться условие

∑	= 1,	(3.36)
т

которое означает, что полная вероятность всех вантовых состояний равна единице.

Введем квантово-статистический оператор (матрицу плотности), который в матричном представлении (x - представлении) имеет вид

̂( , ′) = ∑				( )	( ′).	(3.37)

Из ортонормированности волновых функций и (3.37) следует, что

∫ ̂( , ) =

∑

=

∑

= 1.

(3.38)

|

Запишем теперь выражение для среднего значения оператора ̂ при помощи

матрицы плотности (3.37):

̂

( )

̂

∫

̂

= ∑

∫

( ) = ∑

( ) ( ) =

,

= (заменим индексы ↔ и подставим

= ∫ (′)

(′) ′ ) =

∑

′

)

′

)

̂

′

=

(

(

( )

( )

≡

,

̂

∑

′

)

′

)

′

≡

,

(

( )

(

( )

=

= ∑

′

( )

′

̂

′

=

,

( )

( )

( )

̂

′

=

′

̂

′

̂

′

′

= ( ( ,

)

∑

(

)

( )) = ̂(

, ) ( ,

)

. (3.39)

̂

Здесь мы ввели матричное x - представление для оператора . Выражение

(3.39) обычно записывают в виде

̂

̂

(3.40)

= ( ̂),

где шпур берется по координатам x. Последняя запись удобна тем, что она не зависит от представления операторов ̂ и ̂. В частности, под шпуром можно понимать сумму по собственным состояниям

̂

̂

= ∑

̂

̂

≡ ∑

.

(3.41)

= ∑

( ̂)

,

47

В квантовой статистике это представление (n-представление) наиболее удобно. Распределение вероятностей для случая статистического равновесия выбирают в виде канонического распределения Гиббса:

	= Ζ−1e− εn,					(3.42)
	̂		1
	Ζ = ∑n e− εn = Spe− ,	=		,	= − ln .	(3.43)

Поэтому, в x – представлении статистический оператор в случае статистического равновесия даётся выражением

̂( ,	′) = ∑		eβ( −εn)		( )	( ′),	(3.44)
а сам оператор
			̂	̂			(3.45)
̂ = Ζ−1e− = e( − ).

Независимыми переменными в каноническом ансамбле Гиббса являются температура T, объём V и число частиц N. Поэтому, при суммировании по квантовым состояниям необходимо учитывать только состояния с заданным числом N, что существенно затрудняет процедуру взятия шпура. Чтобы не связывать себя условием постоянства числа частиц, удобно перейти к большому каноническому ансамблю, где независимыми переменными являются T, V и химический потенциал . Для этого в гамильтониан вводится дополнительный член

̂	̂	̂	,	(3.46)
	−
и накладывается дополнительное условие				̂
			= , из которого определятся

химический потенциал . В этом случае статистический оператор имеет вид

̂ ̂	̂ ̂	(3.47)
̂ = Ζ−1e− (− ) = e(Ω− + ),
где
̂	̂	(3.48)
Ζ = Spe− (−).

В (3.47) величина Ω называется термодинамическим потенциалом системы в переменных T, V и . Теперь в формулах для статистических средних значений можно суммировать по всем состояниям без ограничения на число частиц в системе.

Рассмотрим ансамбль систем с гамильтонианом ̂( ), зависящим от времени. Матрица плотности в этом случае определяется выражением

	̂( , ′, ) = ∑					( , )	( ′, ),	(3.49)
где	не зависят от t. Функции	( , ) являются решениями нестационар-

ного уравнения Шредингера, удовлетворяющими начальному условию

48

	( , )	=0	=	( ).	(3.50)

Таким образом, ̂( , ′, ) =0 = ̂( , ′). Используя уравнение Шредингера в матричном виде

Ψn(x,t)

= ∫ ( , ′) Ψ (x′, t)dx′,

(3.51)

n

где

′

)

= ∑

′

̂

(3.52)

( ,

(

) ( )),

и свойство эрмитовости гамильтониана

( ′, ) = ( , ′), можно полу-

чить уравнение движения статистического оператора в матричной форме

ρ(x,x′,t)

= ∫[ ( , ′′)ρ(x′′, x′, t) − ρ(x, x′′, t) ( ′′, ′)] ′′ .

(3.53)

Это уравнение называется квантовым уравнением Лиувилля.				В оператор-
ной форме оно имеет вид
	ρ	̂	̂	(3.53)
		= ̂	− ̂ .

При помощи оператора ̂ можно вычислить среднее от произведения нескольких операторов

̂	̂		̂		̂	̂		̂		(3.54)
			… .		= ( ̂			… . . ).
1		2			1		1		1

Эти средние значения определяют корреляцию одной или нескольких физических характеристик системы частиц и называются корреляционными функциями.

В квантовой теории особое значение имеет корреляционная функция двух операторов

̂ ̂ = ( ̂ ̂ ̂).

В случае равновесия

̂ ̂	−1				− εn
=		∑	,	e			.	(3.55)

Использование статистического оператора ̂ обеспечивает максимально полное статистическое описание квантовой системы.

49

Литература

1.А.Н. Матвеев, Молекулярная физика, М., Высшая школа, 1981.

2.Д.В. Сивухин, Курс общей физики, том 2 “Термодинамика и молекулярная физика”, М., Наука, 1979.

3.Ландау Л.Д., Лифшиц Е.М., Теоретическая физика, том 5 “ Статистическая физика”, Часть 1, М., Физматлит, 2001.

4.Р. Фейнман, Статистическая механика, М., “Мир”, 1975.

50