KMSF-Chast1-new

Глава 1. Волновые свойства частиц

§1.1. Корпускулярно-волновой дуализм

В начале прошлого века стало понятно, что классическая теория не в состоянии объяснить целый ряд экспериментов (фотоэффект, ядерная модель атома и пр.). В первую очередь это касалось электромагнитной теории света. В 1900г. М. Планк выдвинул идею, что излучение происходит порциями энергии – квантами. Впоследствии было отмечено, что не только излучение, но и поглощение происходит также квантами. В 1905 г. Эйнштейн сформулировал гипотезу световых квантов. Он предположил, что дискретный характер присущ не только процессам испускания и поглощения света, но и самому свету, т.е. свет распространяется в виде дискретных частиц – фотонов. Эта гипотеза не получала должного признания в течение 15-17 лет, несмотря на то, что с её помощью удалось объяснить за это время несколько экспериментов (фотоэффект, границу тормозного рентгеновского излучения и др.). Корпускулярный аспект излучения проявляется наиболее отчетливо в коротковолновой части спектра, где для спектральной плотности равновесного излучения u ,T справедлива формула Вина, а волновой аспект – в длинноволновой, где применима формула Рэлея-Джинса. Закон излучения Планка, который содержит в себе предельные случаи, соответствующие корпускулярному и волновому аспектам, представляет собой диалектический синтез двух, казалось бы несовместимых, теорий и снимает противоречие между ними. Заметим, что термин фотон был введен Дж. Льюисом только в 1926 г.

Фотонная теория света (электромагнитного излучения):

1)	Масса покоя фотона m0 0 ;						(1.1)
2)	Энергия фотона h ;						(1.2)
	(например, для зеленого света 5000Å и 2,5эВ )
3) Скорость фотона всегда равна c . Фотоны движутся со скоростью							c не
	только в вакууме, но и в веществе. “Замедление” света в веществе обу-
	словлено тем, что фотоны поглощаются атомами и вслед затем испус-
	каются вновь. Между актами поглощения и испускания проходит неко-
	торое время, вследствие чего средняя скорость фотонов в веществе
	оказывается меньше c		;
4)	Масса фотона mф					;	(1.3)
		c2
					c2
			3

5) Импульс фотона

	p
		c		c

.

(1.4)

Напомним, что согласно классической электромагнитной теории, бегущая

электромагнитная волна обладает импульсом p , направленным вдоль волно-

вого вектора

k

и пропорциональным энергии волны:

p

c

. Такое соотноше-

ние между энергией и импульсом выполняется и для элементарного кванта

излучения – фотона:

	p
		c

c

. Учитывая, что отношение

c

равно волно-

вому числу k , запишем

		,				(1.5)
			p k .
	Частота	и волновой вектор k характеризуют волновые свойства монохро-
	матического излучения, а энергия			и импульс		– корпускулярные.
					p

§1.2. Волны де Бройля и их экспериментальное подтверждение

В 1924 году Луи де Бройль выдвинул гипотезу, что корпускулярноволновой дуализм носит универсальный характер. Итак, движению частицы массы можно сопоставить волновой процесс с длиной волны де Бройля

		2		2	,	(1.6)
		mv		p

где импульс

			m0 v
	p				.	(1.7)
		1 v 2 c 2

Функцию, определяющую распространение свободных волн и движение свободных частиц, можно записать

		i
Ae i t kr	Ae		Et pr .

Свойства волн де Бройля:

1) Фазовая скорость волн де Бройля определяется

монохроматических

(1.8)

E

mc 2

c 2

vф

,

(1.9)

k

k

p

mv

v

4

где m - релятивистская масса, v - скорость частицы. Поскольку скорость частицы всегда меньше скорости света, то фазовая скорость волн де Бройля

всегда больше скорости света:

				c	2
	v
		ф		v

c

;

2) Групповая скорость волн де Бройля определяется соотношением

v	гр

d 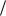dk

,

	v			d		d		dE	v .
		гр		dk		d k		dp

(1.10)

Групповая скорость волн де Бройля совпадает со скоростью самой частицы, которая равна производной энергии по импульсу:

dE		d	m	2	c
dp		dp		0

или

pc

2

pc

2

pc

4

p

2

c

2

p

E

mc

m

c

c

2

4

2

2

0

dp

ds

dE

Fds

dt

ds

v .

dp

dp

dp

dt

2 2

		p	v ,
		m

(1.11)

(1.12)

Произведение фазовой скорости на групповую скорость дает

v		v		c	2	(1.13)
	гр		ф

На основании факта, что групповая скорость равна скорости частицы, некоторое время частицу считали образованием волн де Бройля. Иначе говоря, считали, что волны первичны, а частицы являются их образованием (пакетами волн). Однако оказалось, что не так все просто. Во-первых, фазовая скорость волн де Бройля зависит от скорости частицы v, т.е. зависит от волнового числа k или длины волны . Из-за дисперсии волн де Бройля “частица” получается нестабильной и за время ~ 10-24 секунды расплывается, хотя из опыта мы знаем, что частицы живут весьма долго. Во-вторых, если считать частицы волнами де Бройля, то тогда они должны испытывать дифракцию. При прохождении дифракционной решетки (или кристалла) волновой пакет разлагается на составляющие, что приводит к уничтожению частицы.

Доказательством существования волн де Бройля может служить только эксперимент. Самые яркие явления, характеризующие волны, - это интерференция и дифракция, где наблюдаемой величиной по сути дела является длина волны . Впервые такие эксперименты были поставлены с электронами.Оценим возможные длины волн де Бройля в реальных условиях. Пусть электроны разгоняются в трубке и проходят разность потенциалов U (огра-

5

ничимся нерелятивистским случаем). Тогда кинетическая энергия электрона

равна	E eU	2	mv	2	, а импульс -	p	2meU . Такой электрон обладает длиной
		1

волны де Бройля

		2	.
		2meU

Если длину волны измерять в Ангстремах, а

разность потенциалов в Вольтах, то

		12.25	.
		U

Итак, если электрон прошел

разность потенциалов U = 10 В, то длина волны 3.9 Å. Если U = 100 В, то1.2 Å, и если U = 200 В, то 0.86 Å. При таких условиях длины волн электронов примерно такие же как для рентгеновского излучения и эксперимент по дифракции таких электронов можно ставить как для рентгеновских лучей, а в качестве дифракционной решетки и использовать кристалл.

В методе	Дебая – Шеррера используют поликристаллические пленки
(толщиной 10-5 10-6 см) или порошки. Электроны ускоряются потенциалом U
~ 17.5 56.5	кВ, при этом волны де Бройля ~		0.92 0.52 Å. Поликристалл –
		беспорядочно ориентированные кристаллики. При
=50o		фиксированной длине волны среди множества кри-
		сталликов найдутся такие, для которых выполняется
		условие Вульфа–Брэгга	2d sin m .	Совокуп-
	d	ность кристалликов обладает симметрией вращения
		вокруг направления падающего пучка, вследствие
		этого на экране наблюдаются кольца.
Зная диаметр колец D и расстояние до экрана L можно найти расстояние

между слоями кристаллической решетки d:

	d	D	m .
		2L

L
пучок е-	Изображение на
D	фотопластинке

поликристаллическая пластинка фотопластинка

толщина 10-5 10-6 см

6

§1.3. Статистическое толкование волн де Бройля и соотношение неопределенностей

Рассмотрим интерференционный опыт: пучок электронов падает на экран
						с двумя щелями. На некотором
						расстоянии от щелей на другом
						экране измеряется число элек-
						тронов, попавших в различные
						точки экрана. Пучок может быть
пучок
						такой малой интенсивности, что
						электроны летят и падают на
						экран со щелями поочередно.
						Прямые измерения с “единич-
						ными” электронами (пучками
экран с 2-мя				экран		малой интенсивности) показали,
щелями
						что даже единичные электроны,

когда взаимодействие между электронами не играет никакой роли, дают интерференционную картину. Отсюда напрашивается вывод - отдельные электроны обладают волновыми свойствами. Если закрывать одну или другую щель, то получаем на экране расширенное изображение щели – пунктир на рисунке. Но когда падают одиночные электроны на обе открытые щели, то получаем интерференционную картину. Однако электрон не делится: он проходит либо через одну, либо через другую щель. Если поставим счетчик на фиксирующем экране, то он срабатывает в определенном месте от “целого” электрона и никакой интерференции не увидим. Просто следующий электрон будет зафиксирован в другом месте, за ним другой снова в другом месте и т.д. И там, где амплитуда волнового поля максимальна, там чаще будут регистрироваться электроны, там вероятность нахождения электрона максимальна.

Вероятность всегда связывают с квадратом модуля амплитуды волны

A 2 . Сама амплитуда имеет различные знаки (плюс-минус) и она является неудобной характеристикой для описания интенсивности поля. Исходя из этого, М.Борном была предложена статистическая интерпретация волн де Бройля. Волны де Бройля следует рассматривать как волны вероятности. Интенсивность волн де Бройля в данный момент времени и в данном месте

7

определяет вероятность обнаружить частицу в данное время и в данном месте. А интенсивность волн пропорциональна квадрату амплитуды.

Итак, при прохождении щелей однозначно предсказать, куда попадет электрон, невозможно. Можно лишь определить вероятность этого попадания.

Пусть r ,t дает амплитуду волн де Бройля или, иначе говоря, r ,t - волно-

вая функция, описывающая поведение частицы. Для свободной частицы мы ее уже знаем – это плоская волна

			i
r ,t A exp				Et pr .

Тогда вероятность обнаружить частицу в каком-либо месте пространства

W ~				2		(1.14)
		r , t			.

Для свободной частицы получаем вероятность, не зависящую от координат и

времени W ~ A	2	, т.е. в любом месте пространства нахождение частицы рав-

новероятно. Если частица в находится в силовом поле, то волновая функция

частицы r ,t не есть плоская волна, однако и в этом случае волновая функ-
				2	или
ция дает амплитуду вероятности, причем можно записать dW ~ r ,t
		2	dV,		(1.15)
dW r , t	r , t

где dW – вероятность обнаружить частицу в элементе объема dV. Плотность вероятности

	dW			2	(1.16)
	dV		r , t

Сама волновая функция – ненаблюдаемая величина, она определена с точностью до фазового множителя. Физический смысл связывается с квадратом ее модуля . Если частица существует, то где-то она с достоверностью находится, следовательно, должно выполняться условие нормировки

	2
dW r , t		dV 1.	(1.17)

Отметим, что в случае свободной частицы волновые функции нормируют другим способом.

8

Соотношение неопределенностей. Свободная частица – нелокализован-

ная частица, для которой плотность вероятности равна постоянной	A	2	. Ча-

стицу можно локализовать, если описывать ее пакетом волн. Рассмотрим волновой пакет частицы, локализованной по оси x (при этом амплитуда отлична от 0 на отрезке x):

k0	k
x, t	a k cos k x kx dk .	(1.18)

k0 k

Это соотношение представляет собой разложение локализованной функции по волнам с определенной частотой. Рассмотрим пакет в начальный момент t = 0 и положим a(k) = a(k0) = const во всем интервале (k0 - k k0 + k). Тогда

k

k

sin kx

k

0

k

a k

r , t 0 a k0

0

coskx dk a k0

sin k0

k x sin k

0

k x

0

k

k

x

k

0

k

x

0

2a k

0

sin kx cosk

x .

(1.19)

x

0

Множитель перед косинусом дает медленно меняющуюся амплитуду, которая изображена на рисунке. Основной максимум расположен около точки x = 0 между ближайшими к этой точке нулями. Ближайшие нули определяются sin kx 0 и kx . Отсюда следует, что размер области основной локали-

зации равен

x

2k

, а

x k

2

1

.

Умножая последнее неравенство на постоянную Планка , получаем

соотношение неопределенностей

Гейзенберга		x
p	x ,	(1.20)
x
где x – неопределенность координаты частицы,		px – неопределенность

проекции импульса на ось x. Их произведение не может быть меньше постоянной Планка . При рассмотрении конкретных примеров в правой части неравенства могут стоять различные значения, такие как h = 2 , 4 и т.д. Это зависит от определения неопределенностей x и px. Итак, существует предел в точности одновременного измерения координаты и соответствующей

9

компоненты импульса. Таким образом, нет понятия траектории частицы, что является следствием особой природы частиц микромира (корпускулярноволновой дуализм). Отметим, что в то же время можно измерить одновременно координату x, например, и перпендикулярную компоненту импульса,

	т.е.	x p			y	0.		Из чуть измененного соотношения неопределенностей
	x vx						видно, что чем больше масса частицы, тем точнее можно ис-
				2m

пользовать понятие траектории. Из-за соотношения неопределенностей для координаты и импульса следует, что кинетическая и потенциальная энергии по отдельности не имеют определенного значения.

Рассмотрим для примера телеэкран, на котором фиксируются падающие

электроны.

Если

e

7

,

vx

4

см / с , то ( = 1.054 10

-27

эрг с, m =

v

~ 10 см / с

~ 10

0.9 10-27г)

x ~

1.05 10

27

4

~

~ 10

см , и положение электрона на экране

m v

10

4

0.9 10

27

x

фиксируется с хорошей точностью.

Для электрона в атоме

v

e

~ 10

8

см / с

, а неопределенность координаты элек-

трона по порядку величины совпадает с размером атома x ~ 10-8 см. Тогда

	v	e	~		8	e . Итак, скорость электрона на орбите совпадает с ее
				m x	~ 10 см / с ~ v

неопределенностью и говорить об орбите (траектории) электрона нельзя.

Глава 2. Математический аппарат квантовой механики

§ 2.1. Уравнение Шредингера

Для того, чтобы определить волновую функцию в общем случае ис- r ,t

пользуется основное уравнение нерелятивистской квантовой механики - уравнение Шредингера (1926г.). Оно не выводится, а вводится как новый принцип, который затем проверяется на эксперименте. Это уравнение удовлетворяет требования, которые вытекают из самых общих физических соображений. Во-первых, оно должно быть линейным уравнением, т.к. должен выполняться принцип суперпозиции. Во-вторых, уравнение должно содержать только фундаментальные константы, например e, m, .

Для свободной нерелятивистской частицы

10

		p	2
	E
		2m

k )

С другой стороны, её волна де Бройля ( E ,p

x,t A exp i t kx A exp

i

Et px

Рассмотрим производные:

x,t

i

i

Et px

i

E x,t ,

t

A

E e

x,t

i

p x,t ;

2 x,t

p2

x,t .

x

x2

2

Последнему выражению можно сопоставить следующее равенство

		2	x,t			x,t
			2
	2m		x	2	i	t	.

(2.1)

(2.2)

(2.3)

Это уравнение и является уравнением Шредингера для свободного одномерного движения. Проделанная процедура не есть получение уравнения, а просто наводящие соображения для его написания. Обобщение на трехмерный

случай (свободная частица A exp																	i			) тривиально:
																			Et pr
		2				2					2				2						x, y, z,t
							2					2			2	x, y, z,t i							,	(2.4)
				x						y				z								t
	2m
					2						x, y, z,t i								x, y, z,t
									2													.		(2.5)
																			t
			2m

Исходя из того, что полная энергия частицы во внешнем поле равна

получаем

i	r , t
	t

2

2m

		p	2
	E
		2m

2 r , t

ur , t

U r ,

,

t r , t .

Если ввести оператор Гамильтона - гамильтониан

ˆ	2		2
H				U r , t ,
	2m
				11

(2.6)

(2.7)

(2.8)

то уравнение Шредингера примет вид

i		ˆ	(2.9)
	t	H .

В таком виде мы имеем нестационарное уравнение Шредингера - основное динамическое уравнение нерелятивистской волновой механики. Оно играет такую же важную роль, как уравнения Ньютона в классической механике и уравнения Максвелла в теории электромагнитного поля. Уравнение Шредингера описывает изменение во времени поведения микрообъектов, характери-

зуемых волновой функцией . r ,t

В стационарном случае, когда гамильтониан не зависит от времени, можно разделить уравнение (2.9) на два уравнения - для координатной и временной частей волновой функции. Для этого подставим волновую функцию в виде

r ,t r t									(2.10)
в уравнение Шредингера.
			2					t .
				2					(2.11)
i t r				t r		U r	r
t		2m

Поделив обе части уравнения на полную функцию

, имеем

		t					r
						2	2		U r const E .
	i	t	t							(2.12)
					2m
							r

Левая часть уравнения зависит только от времени t, а правая часть зависит только от пространственных координат. Поскольку это равенство справедливо при произвольных значениях независимых переменных, то обе части уравнения равны константе - константе разделения, которую обозначим через Е. Итак, мы имеем 2 уравнения. Первое уравнение

		t
	i	t	E	(2.13)
		t

имеет решение

t A exp

	i
		Et .	(2.14)

12