
- •Виды матриц:
- •Элементарные преобразования матриц. Правило прямоугольника.
- •Раздел 2
- •Линейные операции над векторами:
- •Свойства:
- •Смешанное произведение векторов: геометрический смысл, свойства. Теорема о смешанном произведении в координатах.
- •Свойства:
- •Виды уравнения прямой: каноническое, в общем виде, проходящей через две данные точки, в отрезках на осях, параметрическое, через угловой коэффициент, через нормальный вектор.
- •Раздел 3
- •Дифференциал функции. Геометрический смысл дифференциала. Теорема о необходимом и достаточном условии дифференцируемости функции.
- •Асимптоты графика функции.
- •Раздел 1
Раздел 3
-
Предел функции. Теоремы о пределах (предел суммы, предел произведения, предел частного, переход к пределу в неравенстве).
Предел функции - такая величина, к которой стремится значение рассматриваемой функции при стремлении её аргумента к данной точке.
Теорема 1. Предел алгебраической суммы двух, трех и вообще определенного числа функций равен алгебраической сумме пределов этих функций.
Теорема 2. Предел произведения двух, трех и вообще конечного числа функций равен произведению пределов этих функций.
Теорема 3. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля
Предельный
переход в неравенстве. Пусть
в некоторой выколотой δ – окрестности
точки х0 функции f (x)
и g (x)
определены и выполнено неравенство f (x)
< g (x).
Пусть существуют пределы
![]() и
и ![]() .
Тогда
справедливо неравенство А ≤ B.
.
Тогда
справедливо неравенство А ≤ B.
-
Односторонние пределы. Непрерывность функции.
Односторонний предел— предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левым и правым пределами.
Функция называется непрерывной в точке, если:
- функция определена в точке;
- функция имеет конечный предел функции;
- этот предел равен частному значению функции в точке.
-
Точки разрыва и их классификация.
Если в точке функция не является непрерывной, то эта точка называется точкой разрыва функции.
Классификация:
- точка называется точкой разрыва первого рода функции если в этой точке односторонние пределы конечны и не равны между собой;
- точка называется точкой разрыва второго рода функции, если в этой точке, по крайней мере, один из односторонних пределов равен бесконечности или не существует.
-
Неопределенность. Типы неопределенностей и способы их раскрытия.
При вычислении пределов зачастую появляются выражения, значение которых не определено. Такие выражения называют неопределенностями.
Типы неопределенностей:
-

-
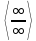
-

-

-

Раскрыть неопределенность можно: - С помощью упрощения вида функции (использование формул сокращенного умножения, тригонометрических формул, дополнительное умножение на сопряженные выражения и последующее сокращение и др. ); - С помощью замечательных пределов; - С помощью правила Лопиталя; - Заменив одно бесконечно малое выражение на эквивалентное ему выражение (как правило, это действие выполняется с помощью таблицы бесконечно малых выражений).
-
Первый замечательный предел.
Предел отношения синуса бесконечно малой дуги к самой дуге, выраженной в радианах, равен единице, т.е.
![]()
Первый замечательный предел:
-
Второй замечательный предел.
Второй
замечательный предел раскрывает
неопределенность
 и равняется числу е.
и равняется числу е.
![]()
Второй замечательный предел:
-
Производная и связь с непрерывностью.
Производная функции - понятие дифференциального исчисления, характеризующее скорость изменения функции в данной точке.
Связь
с непрерывностью.
Если функция ![]() определена
и дифференцируема (имеет производную)
в некоторой окрестности
определена
и дифференцируема (имеет производную)
в некоторой окрестности ![]() ,
то она непрерывна в точке
,
то она непрерывна в точке ![]() .
.
-
Механический смысл производной. Геометрический смысл производной. Уравнение касательной и нормали к кривой.
Механический смысл производной. Скорость – это производная координаты по времени.
Геометрический смысл производной. Производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.
![]()
Уравнение касательной имеет вид:
![]()
Уравнение нормали к кривой имеет вид:
-
Теорема об арифметических операциях над производными.
- производная постоянной функции равна нулю;
-
производная алгебраической суммы
(разности) двух дифференцируемых функций
равна алгебраической сумме (разности)
производных слагаемых:
 ;
;
-
производная произведения двух
дифференцируемых функций равна сумме
произведений производной первого
сомножителя на второй и производной
второго сомножителя на первый:
 ;
;
-
производная частного двух дифференцируемых
функций равна дроби, у которой знаменатель
есть квадрат знаменателя данной дроби,
а числитель представляет собой разность
между произведением знаменателя данной
дроби на производную ее числителя и
произведением числителя на производную
знаменателя:

-
Производной сложной функции.
Сложная функция – это функция, аргументом которой также является функция.
Формула нахождения производной сложной функции:

-
Производная неявной функции. Производная функции, заданной параметрически.
Если
функция
 задана уравнением
задана уравнением
 ,
то говорят, что она задана неявно.
Сначала
необходимо продифференцировать обе
части уравнения по независимой
переменной x,
а после решить полученное уравнение
относительно производной
,
то говорят, что она задана неявно.
Сначала
необходимо продифференцировать обе
части уравнения по независимой
переменной x,
а после решить полученное уравнение
относительно производной  .
.
Зависимость
функции y
от аргумента x
может осуществляться через посредство
третьей переменной t которая
называется параметром. Эта зависимость
имеет вид:
 ,
a
≤ t
≤ b.
В этом случае функция y=y(x)
задана параметрически.
,
a
≤ t
≤ b.
В этом случае функция y=y(x)
задана параметрически.
Первая
производная функции задается формулой:

Вторая
производная функции задается формулой:

-
Правило Лопиталя.
Правило
Лопиталя
представляет собой метод вычисления
пределов, имеющих неопределенность
 или
или
 .
.
Пусть a является некоторым конечным действительным числом или равно бесконечности.
Если
 и
и
 ,
то
,
то

Если
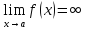 и
и
 ,
то
,
то

Правило
Лопиталя
можно также применять к неопределенностям
типа 0⋅∞,
∞−∞,
00,
1∞,
∞0.
Первые
две
неопределенности
0⋅∞
и
∞−∞
можно
свести
к
типу
 или
или
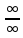 с
помощью
алгебраических
преобразований.
А
неопределенности
00,
1∞
и
∞0
сводятся
к
типу
0⋅∞
с
помощью
соотношения f(x)g(x)=eg(x)lnf(x)
.
с
помощью
алгебраических
преобразований.
А
неопределенности
00,
1∞
и
∞0
сводятся
к
типу
0⋅∞
с
помощью
соотношения f(x)g(x)=eg(x)lnf(x)
.
-
Основные теоремы дифференциального исчисления: Теорема Ферма. Теорема Ролля. Теорема Коши. Теорема Лагранжа.
Теорема Ферма. (О равенстве нулю производной)
Пусть
функция
 удовлетворяет следующим условиям:
удовлетворяет следующим условиям:
-
она дифференцируема на интервале(a;b);
-
достигает наибольшего или наименьшего значения в точке
 .
.
Тогда
производная в этой точке равна нулю, то
есть
 .
.
Теорема Ролля. (О нуле производной функции, принимающей на концах отрезка равные значения)
Пусть
функция
 :
:
-
непрерывна на отрезке [a;b];
-
дифференцируема на интервале (a;b);
-
на концах отрезка [a;b] принимает равные значения
 .
.
Тогда
на интервале (a;b)
найдется, по крайней мере, одна точка
 ,
в которой
,
в которой
 .
.
Теорема Коши. (Об отношении конечных приращений двух функций)
Если
функции
 и
и
 :
:
-
непрерывны на отрезке [a:b];
-
дифференцируемы на интервале (a:b);
-
производная
 на интервале (a:b),
на интервале (a:b),
тогда
на этом интервале найдется по крайней
мере одна точка
 ,
такая, что
,
такая, что
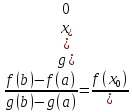
Теорема Лагранжа. (О конечных приращениях)
Пусть
функция
 :
:
-
непрерывна на отрезке [a:b];
-
дифференцируема на интервале (a:b).
Тогда
на интервале (a:b)
найдется по крайней мере одна точка
 ,
такая, что
,
такая, что

