40. Дифференциал функции. Геометрический смысл дифференциала. Теорема о необходимом и достаточном условии дифференцируемости функции.

Дифференциалом функции называется линейная относительно часть приращения функции. Она обозначается как . Таким образом: .

Геометрический смысл. Дифференциал функции в точке равен приращению ординаты касательной, проведенной к графику функции в этой точке, соответствующему приращению аргумента .

Необходимое условие дифференцируемости функции нескольких переменных. Если функция дифференцируема в точке , то она имеет в этой точке частные производные , причем

Достаточное условие дифференцируемости функции нескольких переменных. Если функция имеет частные производные в некоторой окрестности точки , непрерывные в самой этой точке, то она дифференцируема в точке .

41. Производные и дифференциалы высших порядков.

Пусть производная некоторой функции дифференцируема. Тогда производная от производной этой функции называется второй производной функции и обозначается . Таким образом:

Если дифференцируема (n - 1)-я производная функции , то ее n-й производной называется производная от (n - 1)-й производной функции и обозначается . Итак:

Дифференциалом n-го порядка функции называется дифференциал от дифференциала (n - 1)-го порядка этой же функции. Таким образом: .

42. Возрастание и убывание функции. Теорема о необходимом и достаточном условии монотонности.

Функция возрастает на интервале, если большему значению аргумента соответствует большее значение функции.

Функция убывает на интервале, если большему значению аргумента соответствует меньшее значение функции.

Достаточное условие монотонности функции. Если непрерывная на отрезке [а, b] функция у = f(х) в каждой точке интервала (а, b) имеет положительную (отрицательную) производную, то эта функция возрастает (убывает) на отрезке [а, b].

Необходимый признак существования экстремума функции. Если дифференцируемая в точке c функция у = f(х) имеет в этой точке экстремум, то .

43. Экстремум функции. Теорема о необходимом условии экстремума.

Точку называют точкой максимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство . Точку называют точкой минимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство . Точки минимума и максимума называют точками экстремума функции.

Необходимое условие экстремума. Если функция имеет экстремум в точке 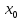, то ее производная либо равна нулю, либо не существует.

44. Выпуклость и вогнутость. Теорема о достаточном условии выпуклости. Точки перегиба.

График функции, дифференцируемой на интервале, является на этом интервале выпуклым, если график этой функции в пределах интервала лежит не выше любой своей касательной.

График функции, дифференцируемой на интервале, является на этом интервале вогнутым, если график этой функции в пределах интервала лежит не ниже любой своей касательной.

Теорема. Пусть дана функция 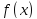, дважды дифференцируема на интервале (a,b). Тогда:

• Если на (a,b), то функция строго выпукла вниз.

• Если на (a,b), то функция строго выпукла вверх.

Точкой перегиба графика функции называется точка, разделяющая промежутки выпуклости и вогнутости.