
- •25. Произведение двух многочленов с целыми коэффициентами.
- •26. Алгебраическая замкнутость поля.
- •27. Основная теорема алгебры.
- •28. Неприводимые над полем комплексных чисел многочлены.
- •29. Неприводимые над полем действительных чисел многочлены.
- •30. Решение уравнений 3 степени. Формулы Кардана.
- •31. Решение уравнений 4 степени. Кубическая резольвента.
- •32. Множество многочленов от нескольких переменных над областью целостности.
- •33. Кольцо многочленов от нескольких переменных над областью целостности.
- •34. Степень многочлена от нескольких переменных.
- •5. Степень произведения многочленов.
- •36. Лексикографическое упорядочение членов многочлена.
- •7. Лемма о высшем члене многочлена.
- •38.Свойства симметрических многочленов.
- •39.Элементарные симметрические многочлены. Теорема Виета.
- •40. Основная теорема о симметрических многочленах.
- •41. Условие при которых многочлены имеют общий корень
- •42. Результант многочленов Решение системы двух уравнений с двумя переменными с помощью результанта.
- •43. Необходимое и достаточное условие существования общего корня у многочленов
25. Произведение двух многочленов с целыми коэффициентами.
Определение: многочлен f(x) с целыми коэффициентами называется примитивным, если НОД всех его коэффициентов равен 1.
Лемма 3. Произведение двух примитивных многочленов также является примитивным многочленом.
Лемма 4:
если многочлен с целыми коэффициентами приводим над
полем Q,
то его можно представить в виде
произведения двух многочленов с целыми
коэффициентами, степень каждого из
которых меньше степени многочлена
.
с целыми коэффициентами приводим над
полем Q,
то его можно представить в виде
произведения двух многочленов с целыми
коэффициентами, степень каждого из
которых меньше степени многочлена
.
до-во: т.к. f(x) –
приводим, то его можно представить в
виде
 ,
,
 ,
,
 ,
,
 и
и
 - многочлены с рациональными коэффициентами.
- многочлены с рациональными коэффициентами.
Пусть
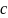 – НОК всех знаменателей коэффициентов
многочленов
и
,
тогда
– НОК всех знаменателей коэффициентов
многочленов
и
,
тогда
 ,
где
,
где
 – многочлены с целыми коэффициентами.
Если
– многочлены с целыми коэффициентами.
Если
 – НОД коэффициентов многочленов
,
то
– НОД коэффициентов многочленов
,
то
 ,
где
–
примитивные многочлены. При необходимости
сократив дробь, представим её в виде
,
где
–
примитивные многочлены. При необходимости
сократив дробь, представим её в виде
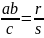 ,
где
,
где
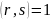 ,
таким образом из
,
таким образом из
 делит все коэффициенты многочлена
делит все коэффициенты многочлена
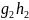 .
По лемме 3 этот многочлен является
примитивным ⇨
.
По лемме 3 этот многочлен является
примитивным ⇨
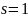 .
.
до-но.
26. Алгебраическая замкнутость поля.
Определение:
поле Р называется алгебраически
замкнутым,
если всякий многочлен из кольца
 степени
степени
 разлагается над полем Р в произведение
линейных множителей.
разлагается над полем Р в произведение
линейных множителей.
Определение: поле Р называется алгебраически замкнутым, если всякий многочлен из степени имеет в поле Р хотя бы один корень.
Покажем, что определения эквивалентны. Пусть поле Р алгебраически замкнуто по первому определению:
 , где
, где
 - элементы поля Р ⇨
- элементы поля Р ⇨
 - это корни ⇨
Р алгебраически замкнуто по второму
определению.
- это корни ⇨
Р алгебраически замкнуто по второму
определению.
 Пусть поле Р
алгебраически замкнуто по второму
определению, т.е. всякий многочлен
из кольца
имеет корень
Пусть поле Р
алгебраически замкнуто по второму
определению, т.е. всякий многочлен
из кольца
имеет корень
 – корень
– корень





Поле Р алгебраически замкнуто по первому определению.
27. Основная теорема алгебры.
Определение:
функция
от комплексной переменной
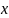 называется непрерывной
в точке
называется непрерывной
в точке
 ,
когда для любого сколь угодно малого
действительного числа
,
когда для любого сколь угодно малого
действительного числа
 существует
существует
 ,
что
,
что
 удовлетворяющего неравенству
удовлетворяющего неравенству
 будет выполнено неравенство
будет выполнено неравенство
 ,
и
,
и
 - действительные
- действительные
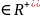 .
.
Функция f(x) называется непрерывной, если она непрерывна в каждой точке области определения.
Лемма 1:всякий
многочлен
из кольца
 является непрерывной функцией.
является непрерывной функцией.
Лемма 2: модуль многочлена из кольца является непрерывной функцией.
Следствие:
если последовательность комплексных
чисел
 сходится к
,
то
сходится к
,
то

Следствие:
если последовательность комплексных
чисел
сходится к
,
то
 ,
то
,
то

Лемма 3(Доломбера):
пусть
многочлен из кольца C[x],
,
если
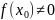 ,
то существует комплексное число C,
что
,
то существует комплексное число C,
что
 .
.
Лемма
4(о
возрастании модуля многочлена): пусть
 - последовательность комплексных чисел
такая что
- последовательность комплексных чисел
такая что
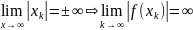
Теорема (основная
теорема алгебры):
всякий многочлен
из кольца
 степени
имеет по крайней мере один комплексный
корень.
степени
имеет по крайней мере один комплексный
корень.
до-во:
Обозначим
через M
множество
всех значений модуля многочлена f
(x)
. Пусть множество М всех значений модуля
многочлена
.
Так как для любого C
– комплексного ,
 – неотрицательное действительное
число, то множество M
ограничено
снизу. Из курса математического анализа
известно, что всякое множество
действительных чисел, ограниченное
снизу, имеет точную нижнюю грань.
Обозначим через l
точную нижнюю грань множества M.
Тогда, в частности, для любого натурального
числа k
можно
подобрать такое комплексное число
,
что
– неотрицательное действительное
число, то множество M
ограничено
снизу. Из курса математического анализа
известно, что всякое множество
действительных чисел, ограниченное
снизу, имеет точную нижнюю грань.
Обозначим через l
точную нижнюю грань множества M.
Тогда, в частности, для любого натурального
числа k
можно
подобрать такое комплексное число
,
что
 .
Если
бы было не так, то
.
Если
бы было не так, то
 ,
,
 и l
не
было бы нижней гранью множества M.
Из (1) следует
и l
не
было бы нижней гранью множества M.
Из (1) следует
 .
Если построенная последовательность
комплексных чисел неограничена, то в
ней можно выделить подпоследовательность,
которая стремится к
.
Если построенная последовательность
комплексных чисел неограничена, то в
ней можно выделить подпоследовательность,
которая стремится к
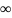 .
.
 .
По лемме 4
.
По лемме 4
 что противоречит (2). ⇨
что последовательность
ограничена. Тогда в ней можно выделить
сходящуюся подпоследовательность,
тогда по лемме 2
что противоречит (2). ⇨
что последовательность
ограничена. Тогда в ней можно выделить
сходящуюся подпоследовательность,
тогда по лемме 2


Если
l
≠
0
, то по лемме 3 существует такое комплексное
число c,
что
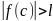 .
.
Это
противоречит тому, что l
–
точная нижняя грань множества M
⇨
l=0
и
 и ⇨
– комплексный корень.
и ⇨
– комплексный корень.
до-но.
