
- •25. Произведение двух многочленов с целыми коэффициентами.
- •26. Алгебраическая замкнутость поля.
- •27. Основная теорема алгебры.
- •28. Неприводимые над полем комплексных чисел многочлены.
- •29. Неприводимые над полем действительных чисел многочлены.
- •30. Решение уравнений 3 степени. Формулы Кардана.
- •31. Решение уравнений 4 степени. Кубическая резольвента.
- •32. Множество многочленов от нескольких переменных над областью целостности.
- •33. Кольцо многочленов от нескольких переменных над областью целостности.
- •34. Степень многочлена от нескольких переменных.
- •5. Степень произведения многочленов.
- •36. Лексикографическое упорядочение членов многочлена.
- •7. Лемма о высшем члене многочлена.
- •38.Свойства симметрических многочленов.
- •39.Элементарные симметрические многочлены. Теорема Виета.
- •40. Основная теорема о симметрических многочленах.
- •41. Условие при которых многочлены имеют общий корень
- •42. Результант многочленов Решение системы двух уравнений с двумя переменными с помощью результанта.
- •43. Необходимое и достаточное условие существования общего корня у многочленов
36. Лексикографическое упорядочение членов многочлена.
Существует способ расположения членов многочлена от нескольких переменных в определённом порядке. Его называют словарным или лексикографическим упорядочением членов многочлена.
Опишем его:
Пусть
 –(1)
–(1)
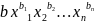 -(2)–
произвольные члены многочлена
с
ненулевыми коэффициентами.
-(2)–
произвольные члены многочлена
с
ненулевыми коэффициентами.
Мы полагаем, что
не содержит подобных членов, поэтому
не все соответствующие показатели
 и
и
 равны
между собой. Пусть
равны
между собой. Пусть
 и
и
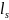 первые из таких показателей, то есть
первые из таких показателей, то есть

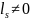 и
=
при
и
=
при
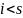 .
Член (1) будем считать выше члена (2) если
.
Член (1) будем считать выше члена (2) если
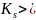 .
Если же
.
Если же
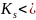 ,
то из двух этих членов будем считать
выше член (2). Иначе говоря, из членов
(1) и (2) будем считать тот выше, у которого
показатель при
,
то из двух этих членов будем считать
выше член (2). Иначе говоря, из членов
(1) и (2) будем считать тот выше, у которого
показатель при
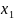 больше. Если же показатели при
равны, то тот из членов будем считать
выше у которого показатель при
больше. Если же показатели при
равны, то тот из членов будем считать
выше у которого показатель при
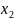 больше и т.д.
больше и т.д.
При словарном упорядочении членов многочлена первым записывается высший член многочлена, вторым – следующий по высоте и так далее.
7. Лемма о высшем члене многочлена.
Лемма 2.1. (о высшем члене многочлена).
Высший член произведения двух многочленов и , отличных от нуля, равен произведению высших членов этих многочленов.
Доказательство.
Расположим члены в многочленах и в словарном порядке.
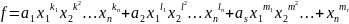 ;
;
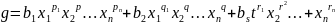 ;
;
Найдём произведение
следующим
образом: вначале умножим последовательно
все члены многочлена,
начиная с первого на первый член
многочлена
.
Очевидно, что при этом словарный
порядк расположения членов не нарушится.
То есть мы получим группу членов,
высшим из которых будет:
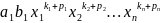 -(3)’
-(3)’
Далее умножим все члены многочлена на второй член многочлена .
Получим группу
членов, высшим из которых будет:
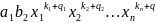 -(3)
и т.д.
-(3)
и т.д.
Наконец, все члены
многочлена
умножим
на последний член многочлена
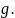 Получим группу членов высшим из которых
будет:
Получим группу членов высшим из которых
будет:
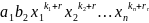
Очевидно, что высший член произведения следует искать среди высших членов найденных групп. Но они в свою очередь составляют группу членов, полученных последовательным умножением многочлена , начиная с первого, на первый член многочлена . При таком умножении словарный порядок расположения членов не нарушится. Следовательно, высшим членом этой группы будет член (3), он же и будет высшим членом произведения . Следовательно, высший член произведения равен произведению высших членов сомножителей и . Теорема доказана.
38.Свойства симметрических многочленов.
Определение:
многочлен
 из кольца
из кольца
 называется
симметрическим,
если в результате любой перестановки
переменных в этом многочлене получается
многочлен равный исходному.
называется
симметрическим,
если в результате любой перестановки
переменных в этом многочлене получается
многочлен равный исходному.
Свойства симметрических многочленов:
1.
сумма, разность и произведение
симметрических многочленов из кольца
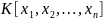 также являются симметрическими
многочленами из этого кольца.
также являются симметрическими
многочленами из этого кольца.
Согласно
приведённому свойству множество
симметрических многочленов образует
подкольцо кольца
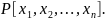
2. пусть
выражение
– (1) является
членом симметрического многочлена
 Тогда членом этого многочлена также
является и всякое выражение, полученное
из (1) в результате перестановки
показателей при переменных.
Тогда членом этого многочлена также
является и всякое выражение, полученное
из (1) в результате перестановки
показателей при переменных.
3.
Пусть выражение (1) является высшим
членом симметрического многочлена
,
тогда выполняются неравенства
 -(2)
-(2)
До-во.
Поменяем местами показатели
 и
и
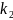 в выражении
(1). Получим выражение: a
в выражении
(1). Получим выражение: a - (3), которое
согласно предыдущему свойству также
является членом многочлена
.
Так как (1) – высший член многочлена,
то, в частности, он выше (2).
- (3), которое
согласно предыдущему свойству также
является членом многочлена
.
Так как (1) – высший член многочлена,
то, в частности, он выше (2).
Отсюда следует,
что
 Поменяем
теперь местами
Поменяем
теперь местами
 в выражении (1), получим также член
многочлена
a
в выражении (1), получим также член
многочлена
a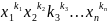 - (4)
- (4)
Учитывая, что (1) –
высший член многочлена, получаем
 и т.д. В конечном
итоге получим неравенства (2).
и т.д. В конечном
итоге получим неравенства (2).
до-но.
