34. Дифференцирование обратной функции.

Теорема 5 (О производной обратной функции). Пусть функции f: X→Y, f^-1: Y→X взаимно обратны и непрерывны в точках x₀ ∈ X и f(x₀) = y₀ ∈ Y соответственно. Если функция f(x) дифференцируема в точке x₀ и f≠0, то функция f^-1 также дифференцируема в точке y₀ , причем (f^-1)’(y₀)=1/f’(x₀).

Доказательство. Из непрерывности f(x) в x₀ и f^-1в y₀ можно заключить, что при x→x₀ , x ∈ X имеем y = f(x) → y₀, y=f(x) ∈ Y и y=f(x)≠ y₀ , если x≠x₀ . Используя теперь теорему о пределе композиции функций и арифметические свойства предела, находим .

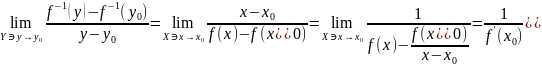Таким образом, показано, что в точке y₀ функция f⁻¹ : Y→X имеет производную и (f^-1)’(y₀)=1/f’(x₀).

Замечание 1. Если бы заранее было известно, что функция f⁻¹ дифференцируема в точке y₀, то из тождества (f⁻¹○f)(x) ≡ x по теореме о дифференцировании композиции функции сразу бы нашли, что (f⁻¹)’ (y₀ )·f’(x₀) = 1.

Замечание 2. Теореме можно дать геометрическую интерпретацию. Как известно, =tgα, где α – значение угла, образуемого касательной графика функции f(x) в точке (x₀, y₀ ) с положительным направлением оси Ox, тогда

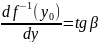, где β – значение угла, образованного той же касательной с осью Oy. Действительно, поскольку β = −α, то

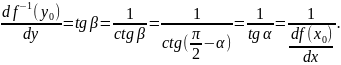
35. Производные и дифференциалы высших порядков 1. Производные высших порядков.

Пусть f : X → Y функция, дифференцируемая в каждойточке x ∈ X. Ее производная в точке x есть некоторая функция g(x) = f’(x). Если функция g(x) дифференцируема, то имеет смысл определить ее производную g’(x) =(f’(x))’, которая называется второй производной функции f(x) и обозначается f’’(x). Таким образом, f’’(x) =(f’(x))’. Аналогично f’’(x) может оказаться дифференцируемой функцией в точке x, тогда f’’’(x)=(f’’(x))’ есть третья производная функции f(x). Точно так же, если в точке x определена производная порядка n−1 функции f(x), то производная порядка n или n-ая производная функции f(x) определяется формулой f⁽ⁿ⁾(x)=(f^(n-1)(x))’ , n=1,2,…

Отметим, что в формуле принято f⁽⁰⁾(x) = f(x), т.е. производная нулевого порядка есть сама функция.

Для n-ой производной функции f(x) применяются и другие обозначения: f⁽ⁿ⁾_xx…x(x), f⁽ⁿ⁾_xⁿ(x), .

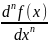Функция f(x) называется n раз дифференцируемой в точке x ∈ X, если в этой точке у нее существуют все производные до n-го порядка включительно.

Если f(x) дифференцируема n раз в каждой точке x ∈ X и f⁽ⁿ⁾(x) является непрерывной функцией на X, то f(x) называется n раз непрерывно дифференцируемой функцией или функцией класса C⁽ⁿ⁾[X]. Множество непрерывных функций, определенных на X, обозначается C[X]. Функция, имеющая производную любого порядка, называется бесконечно дифференцируемой.

2. Дифференциалы высших порядков.

Пусть функция f : X → Y дифференцируема и df = f’(x)dx - ее дифференциал. Дифференциалом второго порядка называется дифференциал от дифференциала первого порядка, который обозначается d²f, то есть d²f = d(df). Дифференциал n-го порядка есть dⁿf = d(d^n-1f).

Если x – независимая переменная, а dx – постоянная (не зависит от x) и функция f имеет n производных, то, учитывая, что (dx)’=(dx)’’=…=(dx)⁽ⁿ⁾=0 последовательно находим: df=f’(x)dx, d²f=d(f’(x)dx)=(f’(x)dx)’dx=f’’(x)(dx)²=f’’(x)dx², … , dⁿf=d(f^(n-1)(x)dx^n-1)=f⁽ⁿ⁾(x)dxⁿ.

Предположим теперь, что x есть некоторая функция параметра t, то есть x = ϕ(t), t ∈ T. Тогда f является сложной функцией f(ϕ (t)) и ее первый дифференциал, как известно, обладает свойством инвариантности формы. Покажем, что дифференциалы более высокого порядка в этом случае инвариантностью не обладают.

В самом деле, если x - независимая переменная, то d²f=f’’_xxdx².

Если же f = f(x), x = ϕ(t), то d²f=d(df)=d(f’_xdx)=df’_x^.dx+f’_x^.d(dx)=f’’_xxdx²+f’_xd²x,

что не совпадает с полученной выше формулой для d²f в случае независимой переменной.