Правило одного шага Жорданого исключения

с разрешающим элементом

1. В новой таблице поменять базисную переменную, стоящую в r-ой строке исходной таблицы и небазисную переменную стоящую в s-ом столбце исходной таблицы

2. Заменить разрешающий элемент на элемент

3. Остальные элементы разрешающей строки делим на разрешающий элемент, те

4. Остальные элементы разрешающего столбца заменить на

5. Элементы, стоящие в i-ой строке и j-ом столбце преобразуются по формуле:

ПРИМЕР

Исходная задача в канонической форме содержит единичный базис. Те таблица без изменений

		3	-1
1		2	1		6	6/2
1		-2	3		9	-
		-3	5		15

			1	-1
	3		1/2	1/2		3
	1		1	4		15
			3/2	13/2		24

Получено оптимальное решение

ЗАМЕЧАНИЯ

1. Если среди относительных оценок несколько отрицательных, то рекомендуется выбирать наименьший отрицательный. Эта оценка определяет разрешающий столбец

2. Если при выборе разрешающей строки минимум достигается для нескольких строк, выбираем любой

3. Сформулированный симплекс метод позволяет за конечное число итераций получить оптимальное решение, либо показать, что задача неразрешима

4. Однако, можно привести пример задачи, с вырожденными опорными решения в к которой идет зацикливание. Зацикливание обходится лексико-графическим порядком.

Метод искусственного базиса

для построение начального опорного решения

Случай 1. Матрица А содержит полный набор единичных столбцов (т.е. содержит базис)

Тогда этот базис является базисом опорного решения.

И начальная симплекс таблица имеет вид

		D
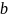
	f

Случай 2. Полный набор отсутствует

Строится вспомогательная задача:

Для простоты будем считать, что нет ни одного единичного столбца

Вспомогательная задача

Вводим в ограничениях равенства искусственные переменные

Искусственные переменные вводятся так, чтобы получить полный набор единичных столбцов.

Далее применяем симплекс метод.

Если оказывается, что , то получаем неразрешимость №1 ( первой задачи.

Если , тогда и оптимальной таблицы строится начальная таблица по определенным правилам

ТЕОРЕМА

Для того, чтобы множество необходимо и достаточно, чтобы

ДОКАЗАТЕЛЬСТВО