Глава 1

=============

КЛАССИЧЕСКАЯ ТЕОРИЯ

ВЕРОЯТНОСТЕЙ

1. Случайные события

1.1. Некоторые формулы комбинаторики

Правило произведения. Если объект А может быть выбран n₁ способами и после каждого такого выбора объект В может быть выбран n₂ способами, то выбор пары А и В может быть осуществлен n₁ n₂ способами. Это правило распространяется и на случай выбора трёх, четырёх и т.д. объектов.

Правило суммы. Если первое событие может произойти n₁ способами, а второе - n₂ способами независимо от первого, то первое или второе события могут произойти n₁+n₂ способами.

Рассмотрим некоторое множество Х, состоящее из n элементов . Будем выбирать из этого множества различные упорядоченные подмножества У из k элементов. Размещением из n элементов множества Х по k элементам назовем любой упорядоченный набор элементов множества Х.

Если выбор элементов множества У из Х происходит с возвращением, т.е. каждый элемент множества Х может быть выбран несколько раз, то число размещений из n по k находится по формуле n^k.

Если же выбор делается без возвращения, т.е. каждый элемент множества Х можно выбирать только один раз, то количество размещений из n по k обозначается и определяется равенством .

Пример. Пусть даны пять цифр: 1; 2; 3; 4; 5. Определим сколько трехзначных чисел можно составить из этих цифр. Если цифры могут повторяться, то количество трехзначных чисел будет . Если цифры не повторяются, то . ◄

Частный случай размещения при n=k называется перестановкой из n элементов. Число всех перестановок из n элементов равно .

Пусть теперь из множества Х выбирается неупорядоченное подмножество У, т.е. два подмножества У₁ и У₂ из k элементов, состоящие из одних и тех же элементов и отличающиеся их порядком будем считать одинаковыми. Сочетаниями из n элементов по k называются подмножества из k элементов, отличающиеся друг от друга хотя бы одним элементом. Общее число всех сочетаний из n по k обозначается и равно

.

В дальнейшем будем считать . Заметим, что справедливо равенство .

Пример. В группе из 27 человек нужно выбрать трех делегатов на профсоюзную конференцию. Найдем сколькими способами это можно сделать

. ◄

1.2. Классическое определение вероятности. Относительная

частота события. Статистическое определение

вероятности. Геометрические вероятности

В этой теме необходимо усвоить три понятия: события, вероятности и относительной частоты появления событий при испытаниях, обратив внимание на свойство устойчивости ее при большом числе испытаний; приобрести навыки в решении задач на вычисление вероятности события по классической формуле.

1. Основным объектом классической теории вероятности является так называемое случайное событие, то есть событие, которое может произойти или не произойти в результате проведенного опыта.

Например, попадание в некоторый объект или промах при стрельбе по этому объекту из данного орудия является случайным событием. Рассмотрим виды событий.

Событие называется достоверным, если в результате испытания оно обязательно происходит.

Невозможным называется событие, которое в результате испытания произойти не может.

Случайные события называются несовместными в данном испытании, если никакие два из них не могут появиться вместе.

Будем говорить, что случайные события образуют полную группу, если при каждом испытании может появиться любое из них и не может появиться какое-либо иное событие, несовместное с ними.

Рассмотрим полную группу равновозможных несовместных случайных событий. Такие события будем называть случаями (исходами). Событие такой группы называется благоприятствующим появлению события А, если появление этого события влечет появление А.

Пример. В урне находится 8 шаров, на каждом из которых поставлено по одной цифре от 1 до 8. Шары с цифрами 1, 2, 3 красные, остальные – черные. Появление шара с цифрой 1 (2 или 3) есть событие, благоприятствующее появлению красного шара. ◄

Числовая величина, характеризующая степень возможности данного события, называется его вероятностью. Если можно пересчитать все возможные исходы проводимого опыта и если ни один из этих исходов не имеет приоритета по сравнению с другими (то есть при большом количестве опытов все исходы наблюдаются с одинаковой частотой), то говорят, что мы имеем дело со схемой случаев.

Будем считать, что — число возможных исходов данного опыта, а — число его исходов, при которых происходит некоторое событие (назовем такие исходы благоприятными или благоприятствующими событию Тогда вероятность события определяется как отношение числа благоприятных исходов к числу возможных:

.

Заметим, что вероятность достоверного события р=1. Вероятность невозможного события р=0. Кроме того из определения вероятности следует, что для любого события А

.

Пример. Из колоды в 32 карты вынуто последовательно без возвращения 2 карты. Найти вероятность того, что обе они — тузы.

Так как первую карту можно извлечь из колоды 32 способами, а вторую — 31 (поскольку в колоде осталась 31 карта), то число возможных исходов опыта . Определим число благоприятных исходов. Первый туз можно выбрать из четырех, имеющихся в колоде, второй — из трех оставшихся. Значит, число благоприятных исходов и искомая вероятность равна

. ◄

Во многих случаях, однако, непосредственный перебор всех возможных исходов опыта затруднителен в силу их большого количества. Для решения таких задач полезно использовать некоторые комбинаторные формулы, в частности, формулу для числа сочетаний. Напомним, что число сочетаний из по , то есть число различных неупорядоченных наборов из элементов, выбранных из имеющихся различных объектов, равно

В частности, если имеется группа из объектов двух видов ( элементов первого вида и — второго), из которых требуется выбрать элементов, среди которых должно быть предметов первого типа и второго, вероятность того, что случайно извлеченная подгруппа имеет нужный состав, определяется так:

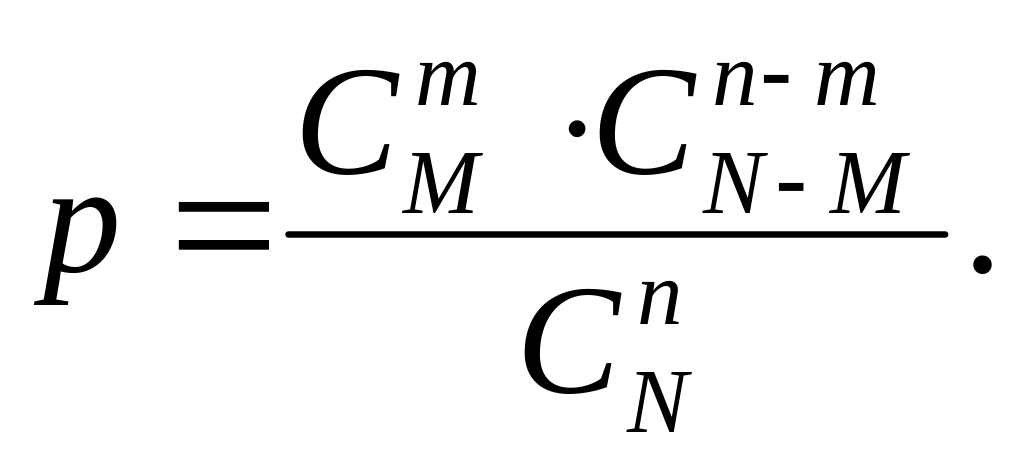
Знаменатель этой дроби представляет собой число возможных исходов опыта, то есть количество различных наборов по элементов, выбранных из имеющихся без учета их качественного состава. В числителе — число благоприятных исходов, представляющее собой число возможных наборов из элементов нужного вида, умноженное на количество возможных наборов из предметов второго типа.

Примеры.

1. В урне 10 пронумерованных шаров с номерами от 1 до 10. Вынули один шар. Какова вероятность того, что номер вынутого шара не превосходит 10?

Пусть событие А – номер вынутого шара не превосходит 10. Число случаев благоприятствующих появлению события А равно числу всех возможных случаев m=n=10. Следовательно, Р(А)=1. ◄

2. В урне 15 шаров: 5 белых и 10 черных. Какова вероятность вынуть из урны синий шар?

Так как синих шаров в урне нет, то m=0, n=15. Следовательно, искомая вероятность р=0. ◄

3. Из колоды в 36 карт вынимается одна карта. Какова вероятность появления карты пиковой масти?

Здесь всего случаев n=36. Событие А – появление карты пиковой масти. Число случаев, благоприятствующих появлению события А, m=9. Следовательно, . ◄

4. Бросаются одновременно две монеты. Какова вероятность выпадения герба на обеих монетах?

Составим схему возможных случаев.

	Первая монета	Вторая монета
1 случай 2 случай 3 случай 4 случай	герб герб не герб не герб	герб не герб герб не герб

Всего случаев 4. Благоприятствующих случаев 1. Следовательно, р=1/4. ◄

5. В урне 10 шаров: 6 белых и 4 черных. Вынули два шара. Какова вероятность, что оба шара белые?

Вынуть два шара из десяти можно следующим числом способов: . Число случаев, когда среди этих двух шаров будут оба белые, равно . Искомая вероятность будет . ◄

6. Из коробки, в которой лежат пять пирожных «эклер» и семь — «наполеон», достали пять пирожных. Найти вероятность того, что среди них два «эклера» и три «наполеона».

Количество возможных исходов опыта представляет собой число сочетаний из 12 по 5:

Число благоприятных исходов является произведением количества способов, которыми можно выбрать два «эклера» из пяти имеющихся, и числа наборов по три «наполеона» из семи:

Следовательно, искомая вероятность равна ◄

7. В цехе работают 6 мужчин и 4 женщины. По табельным номерам наудачу отобраны 7 человек. Найти вероятность того, что среди отобранных лиц три женщины.

Общее число возможных исходов равно числу способов, которыми можно отобрать 7 человек из 10, т.е. . ◄

Найдем число исходов, благоприятствующих интересующему нас событию: трех женщин можно выбрать из четырех способами; при этом остальные четыре человека должны быть мужчинами, их можно отобрать способами. Следовательно, число благоприятствующих исходов равно .

Искомая вероятность . ◄

8. Пять книг расставляются на полку. Найти вероятность того, что две определенные книги окажутся рядом.

Число всех способов, которыми можно расставить на полке пять книг, равно числу перестановок из пяти элементов .

Подсчитаем число благоприятствующих случаев. Две определенные книги можно поставить рядом 2!=2 способами. Оставшиеся книги можно расположить на полке способами. Поэтому .

Итак, . ◄

2. Статистическое определение вероятности. Недостатком классического определения вероятности является то, что не всегда удается узнать, являются исходы испытания равновозможными или не являются.

Относительной частотой р^* случайного события А называется отношение числа m^* появления данного события к общему числу n^* проведенных одинаковых испытаний, в каждом из которых могло появиться или не появиться данное событие.

.

Оказывается, что при большом числе испытаний n, относительная частота появления события А в различных сериях отличается друг от друга мало и это отличие тем меньше, чем больше испытаний в сериях.

При статистическом определении вероятностью события называют относительную частоту события при большом числе испытаний или число близкое к ней:

.

3. Геометрический метод вычисления вероятностей. Если множество возможных исходов опыта можно представить в виде отрезка прямой или в виде некоторой плоской или трехмерной области, а множество исходов, благоприятных событию — как часть этой области, то вероятность рассматриваемого события определяется следующим образом:

где — длина отрезка (площадь или объем области), задающего множество возможных исходов, а — соответствующая мера множества благоприятных исходов.

Пример. В круг наудачу брошена точка. Найти вероятность того, что она не попадет в правильный треугольник, вписанный в этот круг.

В этом случае мерой множества возможных исходов является площадь круга: а мерой множества благоприятных исходов — разность площадей круга и треугольника: . Следовательно, вероятность заданного события равна

◄

Вопросы для самопроверки

1. Что понимается под событием? Как подразделяются события?

2. Какие события называются элементарными или случаями?

3. Сформулируйте аксиомы теории вероятностей и следствия из них

4. Сформулируйте классическое определение вероятности события. Укажите возможные границы вероятности.

5. Что такое относительная частота появления события или частость? В чем состоит свойство статистической устойчивости относительной частоты? В чем состоит различие между вероятностью и относительной частотой?