1. Предмет теоретической механики состоит в изучении и предсказании движений материальных систем. С этой целью формулируются законы механики, создаются и анализируются соответствующие математические модели. Понятие аффинного точечно-векторного пространства представляет собой математическую модель простейших геометрических объектов и их отношений, на которых базируется теория движения.
Предмет теоретической механики состоит из трех разделов: статики, кинематики и динамики.
Предметом теоретической механики являются материальные тела, представленные своими простейшими моделями и рассматриваемые в связи с изменением их взаимного расположения в пространстве и времени. Такое внешнее движение моделей тел, рассматриваемое в отвлечении от внутренних, молекулярных, атомных и других подобных скрытых движений материи в действительных телах, называют механическим движением и противополагают общим движениям материи ( тепловым, электрическим, магнитным и другим), изучаемым в физике.
Материальной точкой называют тело, размерами которого можно пре-небречь. Она обладает массой и способностью взаимодействовать с другими материальными точками. Например, в небесной механике планеты, движущие-ся вокруг Солнца, часто рассматривают как материальные точки, поскольку их размеры малы по сравнению с размерами орбит. Пользоваться понятием мате-риальной точки целесообразно также и в том случае, когда все частицы движу-щегося физического тела перемещаются одинаково. Совокупность материальных точек, положения и движения которых взаимосвязаны между собой, называется системой материальных точек. В теоретической механике пренебрегают малыми деформациями тел и считают эти тела абсолютно твердыми. Абсолютно твердым телом называется такое тело, расстояние между дву-мя точками которого, во все время движения, остается величиной постоянной. Силой называется количественная мера механического взаимодействия тел. Сила является векторной величиной, действие силы на тело определяется численным значением (модулем), направлением и точкой приложения силы
2. Аксиома 1. Две силы, действующие на абсолютно твердое тело уравновешива-ются только тогда, когда они равны по величине и направлены по од-ной прямой в противоположные стороны (рис. 1.2).
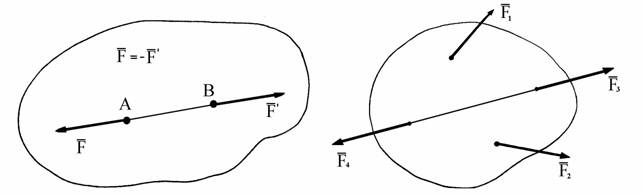
Рис. 1.2 Рис. 1.3
Аксиома 2. Действие данной системы сил на абсолютно твердое тело не изме-нится, если
прибавить к ней или отнять от нее
уравновешенную сис-тему сил
(рис.
1.3).
Следствие из аксиомы 1 и
2. Действие силы на абсолютно твердое
тело (АТТ) не изменится, если точку
приложения этой силы перенести по ли-нии
ее действия. Пусть на тело в точке А
действует сила 
(рис.
1.4). Добавим в точке В, выбранной произвольно
на линии действия си-лы
,
уравновешенную систему сил 
и 
равных
по абсолютной величине
и
направленных по линии ее действия. На
основании аксиомы 1 силы
и
будут
уравновешены и их можно отбросить
(аксиома 2). В результате получим
силу
=
,
но приложенную не в точке А, а в точке
В. Отсюда следует, что сила, приложенная
к АТТ, есть вектор скользящий.
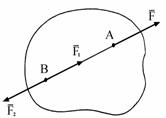
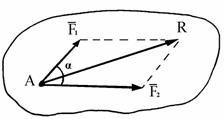
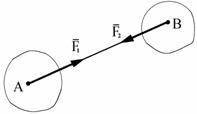
Рис. 1.4 Рис. 1.5 Рис. 1.6
Аксиома 3 Равнодействующая двух сил, приложенных к АТТ в одной точке, равна
их геометрической сумме
, т.е. выражается по моду-лю и направлению
диагональю
параллелограмма,построенного на этих силах (рис. 1.5).
Аксиома 4 Всякому действию одного тела на другое соответствует равное по величине,
но противоположное по направлению противодействие. Действие и противодействие-это силы,
приложенные к двум раз-личным телам, поэтому они не уравновешиваются (рис. 1.6).
Аксиома 5 Если деформируемое тело под действием системы сил находится в
равновесии, то при отвердевании его равновесие сохраняется.
Под действием сил тело D находится в равновесии. Если трос CB заменить стержнем,
то равновесие не нарушится, равновесие не нарушится и в том случае, если трос BD
за-менить стержнем, если же стержень АВ заменить тросом - равновесие нарушится
(рис. 1.7).
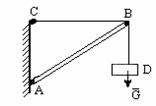
Рис.1.7
3. Связи и их реакции. Твердое тело называется свободным, если оно мо-жет перемещаться в пространстве в любом направлении (ВС в полете). Тело, ограничивающее свободу движения данного твердого тела, является по отно-шению к нему связью. Твердое тело, свобода движения которого ограничена связями, называется несвободным (движение самолета по ВПП). Сила, с которой связь действует на тело, препятствуя его перемещению в том или ином направлении, называется силой реакции этой связи. Для нахождения реакции связей используют аксиому связей, на основании ко-торой всякое несвободное тело можно рассматривать как свободное, если от-бросить связи, заменив их действие на тело силами реакций этих связей. Направление силы реакции связи противоположно тому направлению, в котором активные силы стремятся переместить тело.
Различают три группы связей:
1. Гибкие связи (трос, цепь, ремень, канат).
Реакции связей направлены по оси связей
(рис. 1.8).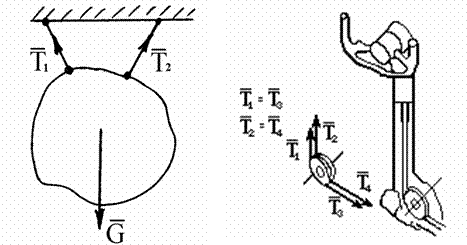 
Рис. 1.8
Если нить отклоняется роликом, в котором не учитывается трение, то натя-жение нити не изменяется.
Например, натяжение тросов, идущих от штурвала к элеронам самолета, с обеих сторон равны по модулю
|Т1|= |Т3|, |Т2|= |Т4| (рис. 1.8б).
2. Твердые, идеально гладкие связи. Реакция направлена по общей нор-мали к поверхностям
соприкасающихся тел (рис. 1.9).
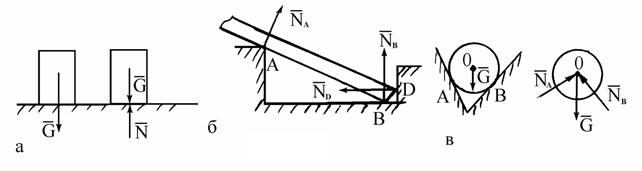
Рис. 1.9
3. Шарнирные связи. Шарниром в механике называется устройство, до-пускающее поворот одного тела
относительно другого, но ограничивающее при этом линейные перемещения этих тел. Шарнирами,
например, являются соеди-нения А, В, С элементов задней опоры самолета (рис. 1.10), узлы А,В,С,D
под-вески авиационного двигателя (рис. 1.11).
Реакция
цилиндрического шарнира 
может
иметь любое направление в плоскости,
перпендикулярной оси шарнира. Направление
реакции зависит от ве-личины и направления
действующих на тело сил. Реакция
подвижного шарнира всегда направлена
по нормали к опорной поверхности шарнира
(рис. 1.12б, в). 
Рис. 1.12
Шаровой шарнир исключает любое перемещение тела во всех направле-ниях, кроме вращения, поэтому
реакция шарового шарнира может иметь любое направление в пространстве. Чаще всего эту реакцию
представляют в виде трех ее составляющих по осям координат x, y, z (рис. 1.13).
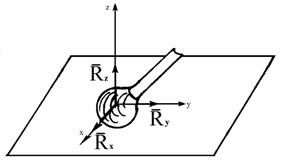
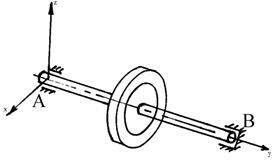
Рис. 1.13 Рис. 1.14
Разнообразные опорные устройства валов машин схематически представ-ляют подшипниками двух типов:
радиальным (цилиндрическим - А), не пре-пятствующим некоторым осевым смещениям вала и радиально-
упорным (В), исключающим осевые перемещения вала (рис. 1.14).
Неподвижная защемляющая опора или жесткая заделка. На заделанный конец балки со стороны опоры
действует система распределенных сил, кото-рую заменяем эквивалентной системой сосредоточенных сил
и
моментом Ма, приложенных в точке А (рис.
1.15).
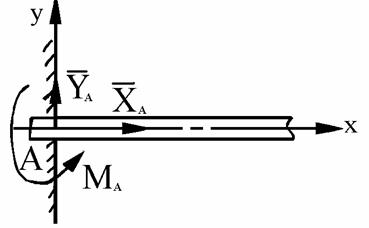
Рис. 1.15
4. Сложение сходящихся сил. Система сил, линии действия которых пересекаются в одной точке,
называется системой с х о д я щ и х с я с и л.
Сложить две или несколько сил - это значит заменить эти силы одной силой, им эквивалентной, т.е.
найти их равнодействующую (рис. 1.16).
Из
ADC:
т.к.
Найти равнодействующую можно также,
построив половину параллело-грамма -
треугольник сил, в котором равнодействующая
является замыкающей стороной (рис.
1.17).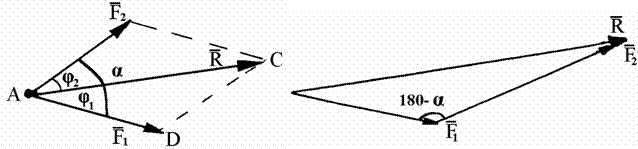 
Рис. 1.16 Рис. 1.17
Равнодействующая трех сил приложенных
в одной точке и не лежащих в одной
плоскости, равна по модулю и направлению
диагонали параллелепипеда, построенного
на этих трех силах (рис. 1.18). Так как 
,
а 
,
то получим
Равнодействующая нескольких сходящихся сил выражается по модулю и на-правлению вектором, соединяющим начальную и конечную точки ломаной ли-нии (правило силового многоугольника) (рис. 1.19).
или
Сходящиеся силы уравновешиваются
в случае, если их равнодействую-щая
равна нулю, т.е. многоугольник сил
замкнут. Конец вектора последней си-лы
совпадает с началом вектора первой
силы, все силы направлены по контуру
многоугольника в одну сторону 
Аналитическое условие равновесия. При
R = 0 получим
где
-
проекции сил на координатные оси.
Следовательно,
Для равновесия тела при действии на
него пространственной системы сходящихся
сил необходимо и достаточно, чтобы сумма
проекций этих сил на каждую из координатных
осей была равна нулю.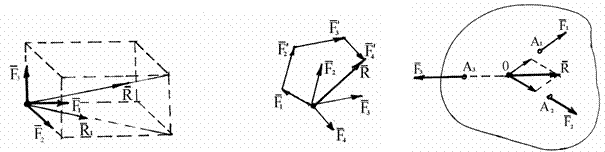 
Рис. 1.18 Рис. 1.19 Рис. 1.20
Теорема о равновесии трех непараллельных сил.
Линии действия трех непараллельных
взаимно уравновешивающихся сил, лежащих
в одной плоскости, пересекаются в одной
точке. К твердому телу в точках А1 , А2 ,
А3 приложены три непараллельные взаимно
уравновешивающиеся силы 
,
лежащие в одной плоскости. Перенесем
силы
и
в
точку О и найдем их равнодействующую.
Сила 
будучи
уравновешивающей системы сил
и
, равна по модулю их равнодействующей
и направлена по линии ее действия в
про-тивоположную сторону (рис. 1.20).
5. Момент силы относительно центра. Опыт
показывает, что эффект дей-ствия силы,
приложенной к телу (например, к рычагу,
штурвалу) на разных расстояниях от точки
закрепления тела, зависит от так
называемого м о м е н т а
с и л ы
относительно точки закрепления.
Моментом
силы 
относительно
центра О называется произведение модуля
силы на кратчайшее расстояние от центра
О до линии действия силы.
(1.6)
где h - кратчайшее расстояние от центра О до линии действия силы Момент силы считается положительным, если сила стремится повернуть тело вокруг центра О против хода часовой стрелки и отрицательным, если по ходу часовой стрелки (рис. 1.24, 1.25). Размерность момента силы Н*м.
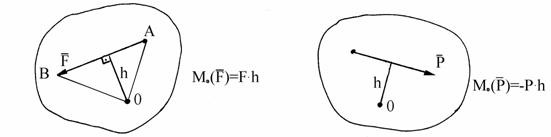
Рис. 1.24 Рис. 1.25
Момент силы не изменяется при переносе точки приложения силы вдоль ее линии действия. Момент силы относительно центра О равен нулю, если сила равна нулю или, если линия действия силы проходит через центр О (плечо рав-но нулю). Графически абсолютная величина момента силы относительно центра О вы-ражается удвоенной площадью ОАВ
= 2S ОАВ
Момент силы относительно центра как
векторное произведение. Введенного
понятия "момент силы относительно
центра как алгебраическая ве-личина"
оказывается недостаточно в случае сил,
произвольно расположенных в пространстве.
Плоскости поворота у разных сил будут
различными и должны задаваться
дополнительно. Удобно ввести понятие
"момент силы относительно центра как
в е к т о р", модуль которого равен
произведению модуля силы на ее плечо,
а направление перпендикулярно плоскости,
проходящей через линию действия силы
и центр момента.
Вектор момента
силы
прикладывают
в центре момента и направляют в сторону,
откуда сила видна вращающей тело в
направлении, противоположном ходу
часовой стрелки (рис. 1.26). Соединим центр
момента О с точкой приложения силы
радиусом-вектором и найдем векторное
произведение 
По определению векторного произведения его модуль | |= 2S ОАВ
Модуль вектора момента силы 
акже
равен удвоенной площади
ОАВ
=
Направление векторного произведения
также совпадает с направлением вектора
момента. Следовательно,
вектор-момент
силы
относительно
центра О можно рассматривать как
векторное произведение
радиус-вектора
проведенного
из этой точки в точку приложения силы,
на вектор силы
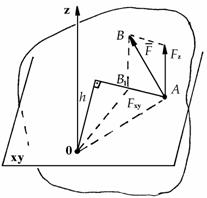
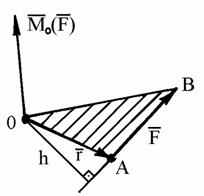
Рис. 1.26 Рис. 1.27
6. Теорема Вариньона: Если система сил, приложенных к абсолютно твердому телу имеет равнодействующую, то момент равнодействующей относительно произвольного центра (оси) равен сумме моментов всех сил системы относительно того же центра (оси).
Векторная запись теоремы:
.
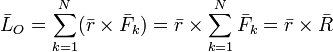
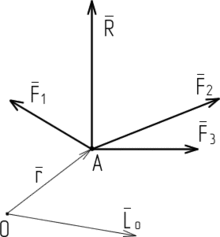
7,8.
Основные положения. Кинематика - раздел теоретической механики, в котором изучается механическое движение, без учета масс и приложения сил. Всякое движение тел происходит в пространстве и во времени, по отношению к другим телам, с которыми жестко связывают систему координат, называемую системой отсчета. Абсолютно неподвижных тел в окружающем нас мире нет, поэтому движение и покой любого тела являются относительными. При изучении движения самолета по аэродрому или при полетах на небольшие расстояния Землю считают неподвижной и связывают с ней систему отсчета. При скоростных полетах на большие расстояния систему отсчета по-прежнему связывают с Землей, но не считают ее неподвижной, а учитывают суточное, а в некоторых случаях и годовое движение. При расчетах движения космических кораблей систему отсчета связывают с Солнцем и так называемыми "непод-вижными" звездами. Для измерения расстояний в пространстве используют единицу длины - метр. Время в механике считают скалярной, непрерывно изменяющейся величиной, одинаковой для всех систем отсчета. За единицу времени принята секунда. Для характеристики рассматриваемого движения в механике пользуются понятиями "траектория точки", "скорость точки" и "ускорение точки". Траекторией называют множество последовательных положений движущейся точки в рассматриваемой системе отсчета. Скоростью точки называют пространственно-временную меру, характеризующую быстроту и направление движения точки. Ускорением точки называют пространственно-временную меру, характеризующую изменение абсолютной величины и направления скорости.
Способы задания движения точки.
Определение скорости и ускорения
точки. Для задания движения точки в
пространстве пользуются каким-либо
одним из трех основных способов:
векторным, координатным,
естественным.
Векторный
способ. Положение точки в пространстве
однозначно определяется заданием
радиуса-вектора 
,
проведенного из некоторого неподвижного
центра О в данную точку М. Для определения
движения точки должна быть задана
вектор-функция
аргумента
t (рис. 1.43):
(1.40)
Траекторией точки является г о д о г р а ф радиуса-вектора. Вектор скорости точки в данный момент времени t равен первой производной от радиуса-вектора точки по времени и направлен по касательной к траектории точки в сторону движения (рис. 1.44).
(1.41)
Размерность [V] = [длина/время] = L/t = м/с. С к о р о с т ь - это векторная величина, характеризующая быстроту и на-правление движения точки в данной системе отсчета. У с к о р е н и е м точки называется вектор, характеризующий быстроту изменения вектора скорости (рис. 1.45)
(1.42)
Ускорение точки равно первой производной от вектора скорости или вто-рой производной от радиуса-вектора точки по времени. Вектор ускорения точ-ки всегда направлен в сторону вогнутости траекториии и лежит в так называемой соприкасающейся плоскости.
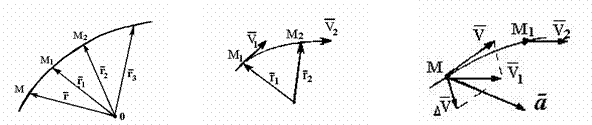
Рис.
1.43 Рис. 1.44 Рис. 1.45
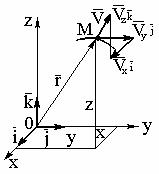Рис.
1.46
Координатный способ. Рассмотрим движение точки в прямо угольной системе декартовых координат. Положение точки М в системе отсчета OXYZ определяется тремя декартовыми координатами точки x, y, z.
уравнения движения точки в декартовых
коорди-натах. Обозначим орты осей
координат 
.
Проведем из начала координат в движущуюся
точку М радиус-вектор
,
где 
,
тогда
где
проекции вектора скорости точки на неподвижные оси декартовых координат. Модуль и направление вектора скорости
V = 
= 
(1.45)
; 
; 
(1.46)
Ускорение точки определяем, зная, что
где
проекции ускорения на координатные оси. Модуль и направляющие косинусы вектора ускорения:
(1.48)
(1.49)
Естественный способ. Движение точки определено, если зада-ны (рис. 1.47): - траектория, положение которой относительно выбранной системы от-счета известно; - начало и направление отсчета дуговой координаты; - уравнение движения
s = f(t), (1.50)
связывающее расстояние S движущейся точки от начала отсчета со временем. В общем случае расстояние S не равно пройденному точкой М пути, так как точ-ка может начать движение не из начала отсчета О, а из другого положения (М1). Численное значение скорости
(1.51)
т.е. равно первой производной по
времени от расстояния. Знак скорости
показывает направление движения точки
в данный момент. При знаке "плюс"
точка движется в сторону положительного
отсчета расстоя-ний и наоборот.
При
естественном способе задания движения
ускорение точки определя-ют его
составляющими, направленными по так
называемым естественным осям. Траектория
точки, как и любая кривая, имеет три
естественные оси (рис. 1.48):
- касательную (орт
оси-
)
направленную в сторону положительно-го
отсчета;
- главную нормаль (орт
оси-
)
- линию пересечения соприкасаю-щейся и
нормальной плоскостей, направленную в
сторону вогнутости кривой;
- бинормаль (орт
оси-
),
перпендикулярную касательной и главной
нормали.
Кривизной К кривой в
данной точке называют предел отноше-ния
угла смежноcти (рис. 1.49) к длине дуги
Величина, обратная кривизне K, называется радиусом кривизны:
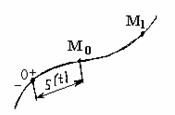
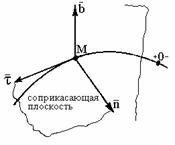
Рис. 1.47 Рис. 1.48 Рис. 1.49
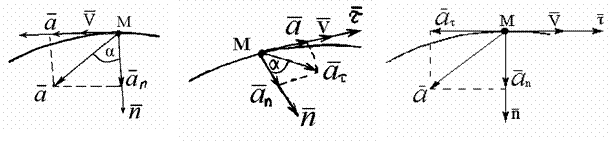
Ускорение точки лежит в соприкасающейся
плоскости и равно производной от вектора
скорости по времени (рис. 1.50). Представим
вектор скорости
как
произведение ее численного значения V
на орт касательный
:
Первое слагаемое есть касательное ускорение точки, характеризующее изменение вектора скорости этой точки только по модулю:
Рассмотрим второе слагаемое.
Величину 
найдем,
взяв предел отношения 
Получим 
,где
-
единичный вектор, направленный по
главной нормали, p- радиус кривизны
траектории.
Тогда 
-
составляющая ускорения точки вдоль
главной нормали к траектории
называется нормальным ускорениемточки
и характеризует изменение направления
вектора скорости:
(1.55)
Нормальное ускорение всегда направлено к центру кривизны траектории Полное ускорение
(1.56)
Модуль ускорения и его направление определяют по формулам:
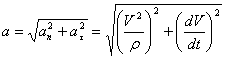(1.57)
или
(1.58)
(1.59)
а б
Рис. 1.50
Рис. 1.51
Движение точки будет ускоренным (рис. 1.51а), если направление векторов скорости и касательного ускорения совпадает, и замедленным (рис. 1.51б), если наоборот. Прямолинейное равномерное движение точки - единственный вид движения, при котором ускорение точки равно нулю
Прямолинейное неравномерное движение точки характеризуется изме-нением скорости по модулю
Криволинейное и равномерное движение точки - происходит изменение направления скорости
Криволинейное неравномерное движение точки
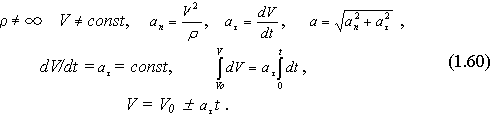
Скорость и уравнение равнопеременного движения точки
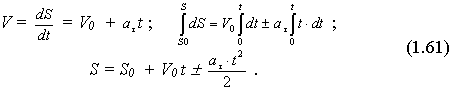
Уравнение равнопеременного движения
точки при 
10.
Простейшие виды движения твердого тела
Поступательное движение. Поступательным
называется такое движение твердого
тела, при котором любая прямая, соединяющая
две точки тела, дви-жется параллельно
самой себе. Траектории точек твердого
тела могут быть лю-быми кривыми
линиями.
Теорема: При поступательном
движении твердого тела все точки
дви-жутся поступательно, описывают
одинаковые траектории (совпадающие при
наложении) и в каждый момент времени
имеют равные скорости и ускорения.
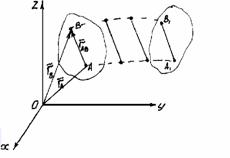
Докажем
эту теорему. Пусть твердое тело совершает
поступательное движение относительно
системы отсчета OXYZ. Положение точек А
и В опре-делено радиусами-векторами 
и 
соответственно,
а положение точки В относительно точки
А - радиусом-вектором 
.
Тогда 
,
где
=
const, учитывая, что 
и 
тогда 
,
но 
Следовательно |
|=|
|
(1.62)
Взяв производные от скоростей обеих
точек, 
или
|
|=|
|
Таким образом, доказано, что
поступательное движение твердого тела
есть простейшая форма движения. Изучение
этого движения сводится к изу-чению
движения точки.
Вращательное
движение твердого тела. В р а щ а т е
л ь н ы м называ-ется такое движение
твердого тела, при котором остаются
неподвижными все его точки, лежащие на
некоторой прямой, называемой осью
вращения (колен-чатый вал поршневого
двигателя, центробежный компрессор,
газовая турбина реактивного двигателя,
винт самолета вращаются вокруг неподвижных
осей). Угол, отсчитываемый от неподвижной
полуплоскости против движения часовой
стрелки, измеряемый в радианах, называется
у г л о м п о в о р о т а т е л а - 
.
Уравнение вращения тела вокруг неподвижной
оси выражает зави-симость угла поворота
от времени (рис. 1.53):
(1.64)
Основными характеристиками
вращательного движения тела являются
угловая скорость - 
и
угловое ускорение - 
.
(1.65)
Размерность [
]
= [рад/с] =[ 
]
.
Величина, характеризующая
быстроту изменения угла поворота с
течением времени, называется угловой
скоростью тела -
.
Угловую
скорость тела можно изобразить в виде
вектора 
,
численная величина которого равна 
и
который направлен вдоль оси вращения
тела в ту сторону, откуда вращение видно
происходящим против хода часовой стрелки
(рис. 1.54а). Такой вектор сразу определяет
и модуль угловой скорости, и ось вращения,
и направление вращения вокруг этой
оси.
В технике угловую скорость
часто выражают не в радианах в секунду,
а частотой вращения n, выраженной числом
оборотов в минуту. Зависимость между n
и
с
учетом того, что каждый оборот
содержит 
рад,
имеет вид
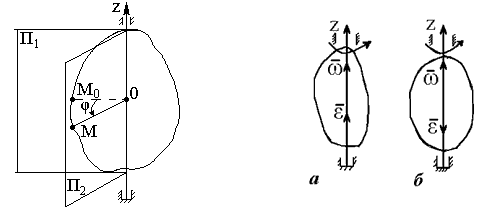
Рис. 1.53 Рис. 1.54
Угловое ускорение тела (по аналогии
с угловой скоростью) можно также
изобразить в виде вектора 
,
направленного вдоль оси вращения. При
этом направление
совпадает
с направлением 
,
когда тело вращается ускоренно и
противоположно
при
замедленном вращении (рис. 1.54а, б).
[рад/
]
(1.66)
Величины 
n
являются угловыми характеристиками,
применимы-ми для всего тела в целом. Их
нельзя относить к отдельной точке
вращающегося тела или к другой какой-либо
точке. Движение точки характеризуется
линейными величинами: скоростью 
и
ускорением 
.
Равномерное
вращение При равномерном вращении
тела постоянна его угловая скорость
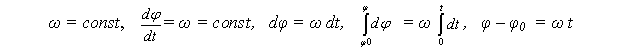
или
(1.67)
Равнопеременное вращение. При равнопеременном вращении постоянно угловое ускорение
(1.68)
(1.69)
При 
и 
получим 
Скорости
и ускорения точек тела, при вращательном
движении. Рассмотрим какую-нибудь точку
М твердого тела, находящуюся на расстоянии
R от оси вращения OZ (рис. 1.55). При вращении
тела точка М будет описывать окружность
радиуса R, плоскость которой перпендикулярна
к оси вращения, а центр С лежит на самой
оси. Если за время dt происходит элементарный
поворот тела на угол 
,
то точка М при этом совершит вдоль своей
траектории элементарное перемещение 
.
Тогда скорость точки будет равна
или
(1.70)
Скорость V называют линейной или окружной скоростью точки М.
Касательное и нормальное ускорения
или
(1.71)
Модуль полного ускорения
(1.72)
и угол 
между
вектором полного ускорения и главной
нормалью траектории
(1.73)
11.12.13.14.
Уравнения плоскопараллельного движения. Разложение движения на поступательное и вращательное.Плоскопараллельным (или плоским) называется такое движение твердого тела, при котором все его точки перемещаются в плоскостях, параллельных некоторой неподвижной плоскости. Рассмотрим сечение тела какой-нибудь плоскостью OXY, параллельной неподвижной плоскости П (рис. 1.56).
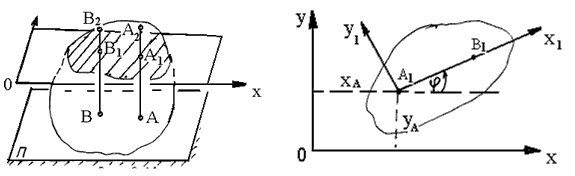
Рис. 1.56 Рис. 1.57
При
плоскопараллельном движении все точки
тела, лежащие на прямой 
,
перпендикулярной к сечению, т.е. к
плоскости П, движутся тождественно.
Поэтому для изучения движения всего
тела достаточно изучить, как дви-жется
сечение тела в плоскости OXY. В дальнейшем
будем плоскость OXY совмещать с плоскостью
рисунка, а вместо всего тела изображать
только его сечение.
Положение
сечения в плоскости OXY определяется
положением какого-нибудь проведенного
в этом сечении отрезка АВ (рис. 1.57).
Положение отрезка АВ можно определить,
зная координаты 
точки
А и угол
,
который от-резок АВ образует с осью
x.
Точку
А, выбранную для определения положения
сечения, называют полюсом. При движении
тела величины
и
будут
меняться:
(1.74)
Уравнения (1.74), определяющие закон происходящего движения, называются уравнениями плоскопараллельного движениятвердого тела. Плоскопараллельное движение можно представить состоящим из поступательного и вращательного движений. Сечение тела (рис. 1.58) можно переместить из одного положения в другое, переместив сначала поступательно и затем повернув на угол вокруг оси, проходящей через полюс (точку А).
Рис. 1.58 Рис. 1.59
Следовательно,
плоскопараллельное движение тела
слагается из поступа-тельного движения,
в котором все точки тела движутся так
же, как полюс, и из вращательного движения
вокруг этого полюса.
За
полюс можно выбрать любую точку, движение
которой известно. При этом поступательное
движение зависит от выбора полюса, а
величина угла по-ворота и направление
поворота от выбора полюса не зависят
(рис. 1.58).
Скорости
точек тела при плоскопараллельном
движении.
Теорема
1. Абсолютная
скорость 
любой
точки плоской фигуры в каждый данный
момент равна геометрической сумме двух
скоростей: скорости 
про-извольно
выбранного полюса в поступательном
движении плоской фигуры и вращательной
скорости 
во
вращательном движении фигуры относительно
полюса.
Положение
любой точки В тела можно определить
равенством (рис. 1.59)
Взяв производную от обеих частей уравнения по времени получим,
,
где 
-
искомая скорость; 
-
скорость полюса; 
-
скорость точки В при вращательном
движении тела вокруг полюса А при 
Таким
образом
(1.75)
Теорема
2. Проекции
скоростей двух точек плоской фигуры на
ось, про-ходящую через эти точки, равны
и имеют одинаковый знак (рис. 1.60). Зная,
что 
,
спроецируем данное выражение на прямую
АВ, тогда
Теорема
3.
Плоская фигура в каждый момент времени
имеет одну точку, абсолютная скорость
которой равна нулю. Эта точка называется
мгновенным центром скоростей (МЦС),
обозначим ее буквой Р (рис.1.61). Докажем
сущест-вование МЦС
и 
заданы.
Повернем полупрямую АI на 90 в сторону
вращения плоской фигуры. Отложим
отрезок Теорема
3.
Плоская фигура в каждый момент времени
имеет одну точку, абсолютная скорость
которой равна нулю. Эта точка называется
мгновенным центром скоростей (МЦС),
обозначим ее буквой Р (рис.1.61). Докажем
сущест-вование МЦС 
тогда
точка Р и будет искомой.
|
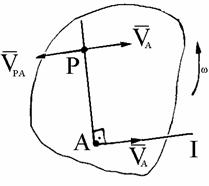
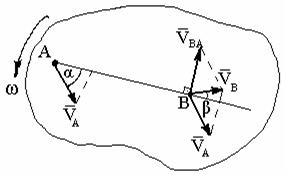
Рис. 1.60 Рис. 1.61
При движении плоской фигуры положение МЦС непрерывно меняется. Графически МЦС находится как точка пересечения перпендикуляров, восста-новленных из двух точек к направлениям их скоростей (рис. 1.62)
Скорости точек плоской фигуры пропорциональны расстояниям от них до мгновенного центра скоростей.
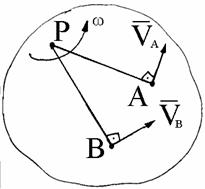
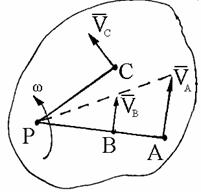
Рис. 1.62 Рис. 1.63
Если за полюс выбран МЦС, то скорость любой точки плоской фигуры есть вращательная скорость вокруг МЦС. Модуль скорости пропорционален расстоянию от точки до МЦС (рис. 1.63).
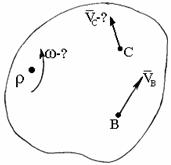
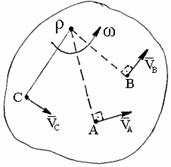
Рис. 1.64 Рис. 1.65
Зная
для данного момента времени положение
МЦС и скорость какой-либо точки В плоской
фигуры, можно определить угловую скорость
и скорость любой точки плоской фигуры
(рис. 1.64).
Если
известна по модулю и направлению скорость
одной точки А и на-правление скорости
другой точки В, то можно определить
скорости всех точек плоской фигуры
(рис. 1.65):
1.
Известно направление и модуль
и
направление
2.
Найдем положение МЦС: проведя перпендикуляры
к векторам скоростей
и
3.
Определим 
4. 
и
т.д.
Частные
случаи определения положения МЦС.
Известны направления скоростей двух
точек. Рассмотрим этот случай на примере
кривошипно-шатунного механизма (рис.
1.66). Направления скоростей точки А
кривошипа и ползуна В известны. МЦС
должен лежать в точке пересечения
перпендикуля-ров к направлениям скоростей
этих точек. Эта точка в бесконечности.
Точка А принадлежит кривошипу и ее
скорость 
,
но точка А также принадлежит и шатуну
АВ. Выберем точку А за полюс, тогда
,
спроецируем на прямую АВ:
Спроецируем векторное равенство на перпендикуляр к АВ:
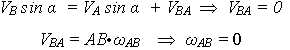
Шатун АВ совершает, так называемое, мгновенно-поступательное движение. Следовательно, если угловая скорость плоской фигуры равна нулю, то МЦС удален в бесконечность и тело совершает мгновенно- поступательное движение. Скорости всех точек плоской фигуры равны по величине и направ-лению. Если скорости двух точек плоской фигуры параллельны между собой и перпендикулярны линии, соединяющей эти точки, то МЦС можно найти из ус-ловия пропорциональности скоростей точек расстояниям от этих точек до МЦС (рис. 1.67).
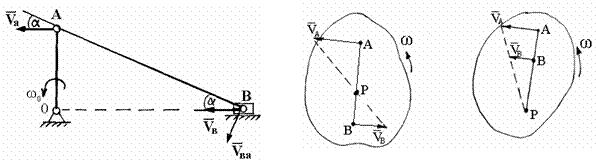
Рис. 1.66 Рис. 1.67
При качении без скольжения одного тела по поверхности другого неподвижного тела МЦС совпадает с точкой соприкосновения тел, так как при отсутствии скольжения скорость точки соприкосновения равна нулю (рис. 1.68).
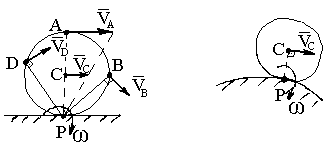
Рис. 1.68 Рис. 1.69
Определение ускорений точек тела. Абсолютное ускорение любой точки В плоской фигуры равно геометрической сумме ускорения полюса А и ус-корения точки В во вращательном движении фигуры вокруг полюса (рис. 1.69).
(1.77)
Движение
плоской фигуры задано 
Ускорение 
точки
В во вращательном движении вокруг полюса
найдем по формулам (1.71) и
(1.72) 
или 
и 
Вектор 
всегда
направлен от точки В к полюсу А,
вектор 
направлен
перпендикулярно ВА в сторону вращения,
если оно ускоренное, и против вращения,
если оно замедленное.
Тогда
вместо равенства (1.77) получим:
(1.78)
15.
Основные понятия, допущения и гипотезы
В статике мы изучали абсолютно твердые тела, которые под действием внешних сил не изменяют размеров и формы. В действительности таких тел нет, все реальные элементы конструкций и машин при действии на них внешних сил изменяют свою форму и размеры - деформируются и при некоторой величине сил могут разрушиться.
Способность деформироваться - одно из основных свойств всех твердых тел. Она является следствием их молекулярного строения. Как известно, твердые тела состоят из молекул, расположенных беспорядочно (аморфное строение) или в определенном порядке (кристаллическое строение). Молекулы не за-полняют всего объема тела, а удерживаются на некотором расстоянии одна от другой под влиянием межмолекулярных сил взаимодействия. Приложение внешних сил нарушает нормальные расстояния между молекулами, и тело деформируется. При этом изменяется нормальное межмолекулярное взаимодействие и внутри тела возникают силы, которые противодействуют деформации и стремятся вернуть частицы тела в прежнее положение. Эти внутренние силы называют силами упругости, а свойство тел устранять деформацию после прекращения действия внешних сил называется упругостью.
Если тело не восстанавливает первоначальной формы и размеров, деформации называют остаточными или пластичными. Наличие остаточных деформаций в деталях машин в подавляющем большинстве недопустимо. Внутренние силы могут увеличиваться лишь до определенного предела, характеризуемого прочностью материала. Если внутренние силы не в состоянии уравновесить внешние нагрузки, тело разрушается.
Для расчета реальной конструкции, установления математических соотношений между действующими силами, геометрическими размерами деталей конструкции, деформациями и силами упругости необходимо отбросить несущественные с точки зрения расчета факторы, т.е. идеализировать конструкцию - создатьрасчетную схему, сохраняющую основные свойства реальной конструкции, но лишенную ее второстепенных свойств.
Основные допущения и принципы, принятые при расчете конструкций:
1. Все тела предполагаются абсолютно упругими.
2. Все тела по своему строению предполагаются сплошными, не имеющими во внутренней структуре трещин или полостей.
3. Материал рассматривается как однородная, изотропная, сплошная среда, обладающая свойством упругости.
Изотропный материал обладает одинаковыми физико-механическими свойствами во всех направлениях (не изотропный материал - дерево, оно по разному сопротивляется нагружению вдоль и поперек волокон).
4. Перемещения точек тела под действием нагрузок очень малы по сравнению с размерами тела, поэтому уравнения равновесия составляются как для недеформируемого тела.
5. Перемещения точек упругого тела прямо пропорциональны действующим нагрузкам.
6. Внешние силы действуют независимо друг от друга. Результат действия на тело нескольких сил равен сумме результатов действия каждой силы, при этом порядок приложения сил безразличен. Это положение известно под названием принципа независимости действия сил.
16.
Метод сечений. Виды деформаций. Напряжения
Будем рассматривать внутренние силы и деформации, возникающие в элементах конструкций, схематизированных в форме бруса (вал двигателя, тяга управления, лонжерон), длина которых значительно превышает их поперечные размеры. Брус может быть прямым (валы, оси, тяги, балки) или кривым (крюк, пружина, звено цепи), иметь постоянное или переменное сечение. Например, подкос шасси самолета считают брусом постоянного сечения, лопатку компрессора ГТД, лопасть воздушного винта - брусом переменного сечения. Кроме стержней (брусьев), могут встречаться пластинки или оболочки, у которых только один размер (толщина) мал по сравнению с двумя другими, и массивные тела, у которых все три размера примерно одинаковы.
Выше отмечалось, что внешние силы, действующие на тело, вызывают в нем внутренние силы упругости. Эти внутренние силы стремятся уничтожить полученную телом деформацию. Обнаружить возникающие в нагруженном теле внутренние силы можно, применив метод сечений. Суть метода заключается в том, что внешние силы, приложенные к отсеченной части тела, уравновешиваются внутренними силами, возникающими в плоскости сечения - заменяющими действие отброшенной части тела на оставленную.
Находящийся в равновесии стержень (рис. 2.1) рассечем на две части. В сечении возникают внутренние силы упругости (рис. 2.1б), уравновешивающие внешние силы, приложенные к отсеченной части. Это позволяет применить к любой отсеченной части тела условия равновесия, дающие в общем случае пространственной системы сил шесть уравнений. В соответствии с правилами статики приведем внутренние силы к главному вектору и главному моменту. Разложим главный вектор и главный момент внутренних сил на составляющие по осям координат (рис. 2.2), где
-
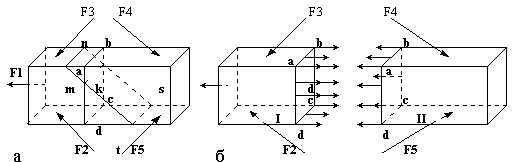
продольная сила; 
и 
-
поперечные силы (срезающие
или сдвигающие); 
-
крутящий момент;Mx и My -
изгибающие моменты.
Рис. 2.1
В частных случаях отдельные силовые факторы могут быть равны нулю. Координатные оси будем направлять следующим образом: ось Z – вдоль оси стержня, а оси X и Y - вдоль главных центральных осей его поперечного сечения.
Внутренние силовые факторы, возникающие в поперечном сечении стер-жня, полностью определяют характер его деформации. Деформации отдельных элементов могут быть сложными, но любую деформацию всегда можно представить как сочетание нескольких простейших деформаций.
Известны следующие простейшие виды деформаций стержней:
- осевое растяжение и сжатие - такой вид деформации, при котором в любом поперечном сечении стержня возникает только продольная сила - (работа тросов, канатов, цепей, тяг управления самолетом, стоек шасси самолета, подкосов рамы двигателя, шатунов поршневых двигателей);
- сдвиг или
срез -
такой вид деформации, при котором в
любом поперечном сечении бруса возникает
только поперечная сила -
(работа
болтов подвижных соединений, цапф,
пальцев сочленения, сварных швов, шпонок
и др.);
- кручение - такой вид деформации, при котором в любом поперечном сечении бруса возникает только крутящий момент - (работа валов, крыла и фюзеляжа самолета, рулей и элеронов, работа стойки шасси);
- изгиб чистый - такой вид деформации, при котором в любом поперечном сечении бруса возникает только изгибающий момент –Mх или My
Если в сечении стержня возникает еще и поперечная сила, то изгиб называют поперечным (работа всякого рода балок, лонжеронов крыла, качалок управления самолетом, ручки управления самолетом, стойки шасси).
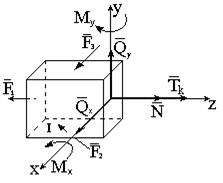
Рис. 2.2
Напряжения. Принято считать, что внутренние силы действуют непрерывно по всему сечению. Мерой их интенсивности является напряжение - величина внутренних сил, приходящихся на единицу площади сечения (рис. 2.3). Напряжение представляет собой отношение внутренней силы к некоторой площади и измеряется в единицах силы, отнесенных к единице площади: 1 H/м2 = 1Па. В практических расчетах удобно измерять напряжения в мегапаскалях (1МПа = 1Н/мм2 = 106 Па = 106 Н/м2).
Через одну и ту же точку тела можно провести бесчисленное множество сечений, разделяющих тело на две части. В общем случае напряжения по различным сечениям будут различны.
Напряжения в некоторой точке какого-либо сечения тела характеризуются числовым значением и направлением, т.е. напряжение представляет собой вектор, наклоненный под тем или иным углом к рассматриваемому сечению. Направление и числовая величина напряжения зависят от характера и величины внешних сил, приложенных к телу, от положения сечения в теле и положения точки в сечении.
Пусть в некоторой точке К сечения тела по некоторой малой площадке А действует сила под некоторым углом к площадке (рис. 2.3).
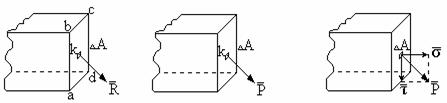
Рис. 2.3
Поделив эту силу на площадь ΔА, найдем возникающее в точке К напряжение
(2.1)
при А 0
Разложим
напряжение 
на
составляющие: 
(сигма)
– нормальное напряжение (по нормали к
площадке Δ А) и касательное напряжение
-
(тау).
Полное напряжение и его составляющие и являются векторами. Рассматривая нормальное или касательное напряжения по какому-либо сечению, мы тем самым точно фиксируем их направление. Поэтому эти напряжения не принято обозначать как векторы. Нормальное напряжение возникает при сближении или отрыве частиц тела, а касательное при скольжении или сдвиге частиц.
При решении задач сопротивления материалов удобнее оперировать не с полным напряжением, а с его составляющими, среднюю величину которых при равномерном распределении нагрузки можно вычислить по формулам:
σ
= 
и = 
(2.2)
Полное напряжение
(2.3)
Напряжение, при котором происходит разрушение материала или возникают заметные пластические деформации, называют предельным, и обозначают σпр, τпр . Эти напряжения определяют опытным путем.
Во избежание разрушения элементов сооружений или машин, возникающие в них рабочие (расчетные) напряжения (σ, τ) не должны превышать так называемых допускаемых напряжений, которые обозначаются буквами в квадратных скобках: [ σ ], [ τ ].
Допускаемые напряжения - это наибольшие напряжения, при которых обеспечивается надежная работа детали
[σ ] = σпр / [n], [ τ ] = τпр / [n], (2.4)
где [n] = 1,2 … 5 и более - коэффициент запаса прочности. Выбор допускаемых напряжений и запаса прочности детали производится с учетом характера действия нагрузок, механических свойств материала, назначения проектируемой конструкции, вида деформации детали, наличия или отсутствия концентрации напряжений, точности расчета и других факторов. Назначение недостаточного запаса может привести к разрушению детали, излишне большой запас приводит к перерасходу материала и утяжелению конструкции.
Опасным напряжением для пластичного материала будет предел текучести σт по которому и берется допускаемое напряжение, опасным же напряжением для хрупкого материала будет предел прочности σВ, тогда
[ σ ] = σТ / [n] и [σ ] = σв / [n] (2.4)
Нагрузка, по которой следует производить расчет на прочность, должна быть больше эксплуатационной, чтобы обеспечить безопасность работы конструкии для этого вводится коэффициент безопасности f – число, показывающее во сколько раз разрушающая нагрузка Fр будет больше эксплуатационной
17.