
- •“Дискретні структури”
- •§1.1. Поняття нечіткої множини
- •§1.2. Операції над нечіткими множинами
- •§1.3. Нечіткі числа
- •§1.4. Операції над нечіткими числами
- •Лекція 3
- •§1.5. Нечіткі інтервали
- •§1.6. Відношення
- •Лекція 5
- •§1.7. Операції над нечіткими відношеннями
- •§1.8. Відображення нечітких множин.
- •§2.1. Основні поняття та означення.
- •§2.2. Зчисленні множини та їх властивості
- •§2.3. Множини потужності континуум.
- •§2.4. Властивості множин потужності континуум.
- •§2.5. Множини, потужність яких є вищою за потужність континуум.
- •§2.6. Порівняння потужностей.
§2.2. Зчисленні множини та їх властивості
Означення 2.2.1. Множина А називається зчисленною, якщо A~N, тобто |A|=|N|.
Приклад 2.2.1. N, {2;4;6;…;2n;…}, {3,6,9,12,…,3n,..} – зчисленні множини.
Теорема 2.2.1. Множина А називається зчисленною тоді і тільки тоді, коли її елементи можна пронумерувати, тобто A~N.
Доведення.
Необхідність(![]() ).
А - зчисленна
A~N
).
А - зчисленна
A~N![]() ,
тобто кожен елемент нумерується аn.
,
тобто кожен елемент нумерується аn.
Достатність(![]() ).
A={a1;a2;…;an;…}
).
A={a1;a2;…;an;…}![]() тоді
приймемо
тоді
приймемо ![]() -зчисленна.
-зчисленна.
Теорему доведено.
Теорема 2.2.2. Із кожної нескінченої множини А можна вибрати зчисленну підмножину.
Доведення.
Шукану зчисленну множину В виберемо так: В={a1;a2;…;an;…}, де a1єА, а2єА\{a1}, a3єА\{a1;a2},…, anєА\{a1,a2,…,an-1}. Теорему доведено.
Теорема 2.2.3. Довільна нескінченна підмножина В зчисленної множини А є зчисленною.
Доведення.
А={a1;a2;a3;…;an;…} і оскільки В⊂А і елементи В можна пронумерувати В – зчисленна множина.
Теорему доведено.
Теорема 2.2.4. Якщо А-зчисленна множина, а В – скінченна множина, причому А⋂В= Ø, то А⋃В є зчисленною множиною.
Доведення.
A={a1;a2;…;an;…},
B={b1;b2;…;bm}.
Пронумеруємо множину А⋃В:
b1
1,
b2![]() ,…,bm
m,
a1
m+1,
a2
m+2,…,
an
m+n,…
,…,bm
m,
a1
m+1,
a2
m+2,…,
an
m+n,…
Теорему доведено.
Теорема
2.2.5. Об’єднання
скінченної кількості зчисленних множин
Аі
![]() таких, що не перетинаються (тобто Ai⋂Aj=
Ø
таких, що не перетинаються (тобто Ai⋂Aj=
Ø ![]() є
зчисленною множиною.
є
зчисленною множиною.
Доведення.
Розглянемо
множини 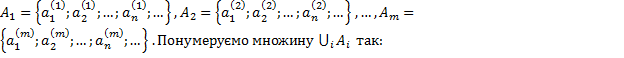
![]()
Теорему доведено.
Теорема 2.2.7. Об’єднанням зчисленної кількості зчисленних множин і таких, що не перетинаються є зчисленною множиною.
Доведення.
Розглянемо множини:
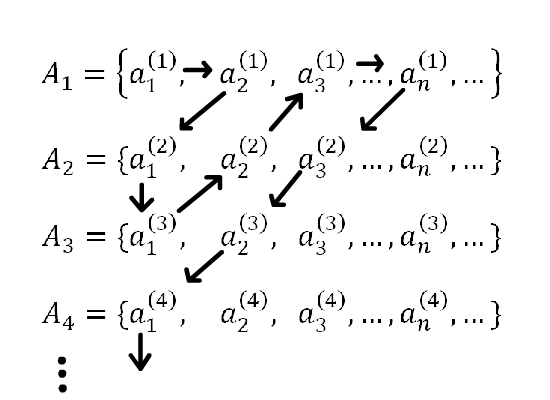
![]()
![]()
Нумерацію
елементів множини ![]() показано стрілками.
показано стрілками.
Теорему доведено.
Зауваження. Умови неперетинності множин у наведених теоремах не зменшують загальності.
Приклад 2.2.2.
Множина раціональних чисел Q є зчисленною. Покажемо це:
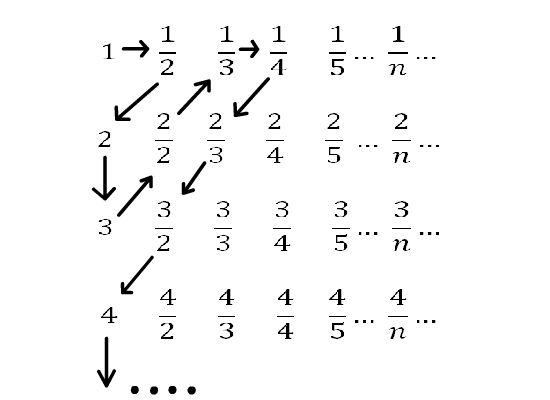
Зображений спосіб нумерації додатних раціональних чисел забезпечує повторення деяких елементів (1, ½, …), а це означає, що Q+ є підмножиною занумерованої множини і за теоремою 2.2.3 Q+ є зчисленною. Оскільки множина відємних раціональних чисел Q- є еквівалентною множині Q+ і Q = Q-⋃Q+⋃{0}, то Q є зчисленною за теоремами.
Множина алгебраїчних чисел є зчисленною (алгебраїчне число – це число, яке є коренем многочлена з цілими коефіцієнтами).
Теорема 2.2.8. Якщо А є нескінченою множиною, а В – зчисленною множиною, то А⋃В є нескінченою множиною, причому А⋃В~A.
Доведення.
А
– нескінченна
![]()
Теорему доведено.
Теорема 2.2.9. Якщо А – нескінченна множина, а В – зчисленна її підмножина і А\В – нескінченна підмножина, то А\В~A.
Доведення.
Множину А зобразимо у вигляді А = (А\В)⋃В. Оскільки А\В – нескінченна, а В – зчисленна, то (А\В)⋃В~A\B (за попередньою теоремою). І тому А~A\B.
Теорему доведено.
Лекція 8
§2.3. Множини потужності континуум.
Теорема 2.3.1. Множина чисел із відрізка [0;1] є незчисленною.
Доведення.
Припустимо, що множина [0;1]
є зчисленною. Тоді всі значення
і відрізка [0;1] можна перенумерувати. У
результаті нехай це будуть {x1;
x2; …
; xn
; …}.
Розіб’ємо відрізок [0;1]
на три рівні частини. Очевидно, що хоча
б одна з отриманих частин не містить
значення х1.
Нехай це буде відрізок [a1;b1],
який знову поділимо на три рівні частини,
при чому одна з яких не містить значення
х2.
Нехай це буде відрізок [a2;b2].
Продовжуючи цей процес далі, отримаємо
![]() тобто
тобто ![]() - послідовність вкладених відрізків,
довжини яких прямують до нуля
- послідовність вкладених відрізків,
довжини яких прямують до нуля ![]() .
За принципом Кантора
.
За принципом Кантора ![]()
З іншого боку, оскільки ![]() ,
то згідно з припущенням
,
то згідно з припущенням ![]()
Приклад 2.3.1. Покажемо,
що множина чисел із напівінтервалу
[0;1) є незчисленною.
Припустимо, що дана множина є зчисленною.
Тоді усі значення з цієї множини можна
пронумерувати. Нехай це будуть
x1=0,a1a2a3a4…;
x3=0,b1b2b3b4…;
x3=0,c1c2c3c4…;
…; xn=0,z1z2z3z4…;…
. Утворимо число
α=0,a1’b2’c3’…zn’…,
![]() та
відрізняється від кожного із занумерованих
чисел
та
відрізняється від кожного із занумерованих
чисел ![]() хоча б однією цифрою . У
зв’язку з цим його немає серед
.
Отримана суперечність доводить
твердження, що напівінтервал [0;1) є
незчисленною множиною.
хоча б однією цифрою . У
зв’язку з цим його немає серед
.
Отримана суперечність доводить
твердження, що напівінтервал [0;1) є
незчисленною множиною.
Означення 2.3.1 Множина А називається множиною потужності континуум, якщо вона є еквівалентною відрізку [0;1].
Приклад 2.3.2. Множини [a;b], (a;b), [a;b), (a;b], R мають потужність континуум, оскільки [0;1]~[a;b]~(a;b)~R.
