
№ 2.3
Условие: есть два заряда, q1 и q2 с радиус векторами r1 и r2, соответственно.
Найти, каким должен быть третий заряд q3, и каким должен быть его радиус-вектор r3, чтобы суммарная сила взаимодействия для всех зарядов была нулевой?

Решение:
Рассмотрим третий заряд: из равенства по модулю действующих на него сил:
![]()
![]()
Решая это квадратное уравнение относительно x, получим:

Из
рисунка видно, что
![]() ,
тогда
,
тогда

Рассматривая первый заряд,
![]()
![]()
№2.5
Два
небольших одинаково заряженных шарика
массой m
подвешены к одной точке на шелковых
нитях, образующих между собой малый
угол
![]() и находятся на одном уровне. Найти
скорость утечки заряда с каждого шарика,
если скорость сближения шариков постоянна
и равна V.
и находятся на одном уровне. Найти
скорость утечки заряда с каждого шарика,
если скорость сближения шариков постоянна
и равна V.
Решение:

l
![]()
x Fk
mg
tg![]() ;
;
Fk=![]() ;
- сила
Кулоновского взаимодействия
;
- сила
Кулоновского взаимодействия
подставим:
![]() ;
;
V=dx/dt=l![]()
Выразим
угол:![]()
Тогда
![]()
Скорость
утечки заряда
![]() ={
={![]() }=
}=![]()
№-2.007.
Тонкое проволочное
кольцо
![]() =100мм
имеет электрический заряд
=100мм
имеет электрический заряд
![]() =50мкКл.Каково
будет приращение силы ,растягивающей
проволоку ,если в центре кольца поместить
точечный заряд
=50мкКл.Каково
будет приращение силы ,растягивающей
проволоку ,если в центре кольца поместить
точечный заряд
![]() =7.0мкКл
?
=7.0мкКл
?
Решение:
![]() ; а
; а
![]() ;
;
![]()
![]() ;
;
Ответ: .
№ 2.9
В вершинах квадрата с диагональю 2l=100 мм находятся одинаковые по модулю (q=2.5мкК) точечные заряды, знаки которых при обходе квадрата расположены в порядке ‘+’,’+’,’-‘,’-‘. Найти напряжённость Е электрического поля в точке, отстоящей на расстоянии х=50 мм от центра квадрата и расположенной симметрично относительно вершин.
Получаем
равнобокую пирамиду с квадратным
основанием. В проекции на высоту получаем
0.А в проекции на основание квадрат с
полудиагоналями
![]()
![]() напряженность от 1 заряда
напряженность от 1 заряда
Суммарное
воздействие
![]()
Ответ:
![]()
2.13. Полубесконечный круглый цилиндр радиуса R заряжен равномерно по поверхности так, что на единицу его длины приходится заряд . Найти напряженность электрического поля в центре основания цилиндра.
Решение:
Разобьем цилиндр на множество колец. В центре основания цилиндра поле перпендикулярно этому основанию т. к. тангенциальные составляющие взаимно компенсируются. Тогда можно проинтегрировать по углу:
Пусть dq – заряд элементa dl длины цилиндра, видимого под углом d, – угол между направлениями на край цилиндра и dl из центра основания, r – расстояние от центра основания до dl,
![]()
![]()
![]()
Ответ:![]() .
.
№ 2.17
Тонкое непроводящее кольцо радиуса R заряжено с линейной плотностью =0cos, где 0 постоянная, - азимутальный угол. Найти модуль напряженности электрического поля :
а) в центре кольца ;
б) на оси кольца в зависимости от расстояния x от до его центра. Исследовать полученное
выражение при x>>R .
Р ешение:
ешение:
а)
Выделем маленький участок кольца dr=Rd
Считая заряд на нем распределенным равномерно, получим
dq=0cosRd;
Разложим составляющие E на Ex и Ey
Ex=EsinEy=Ecos
 ;
;
![]() ;
;
тогда
![]() ;
;
![]() ;
;
![]() ;
;
б)
Р ассмотрим
действие небольшого элемента кольца
dr на расстоянии x
от центра:
ассмотрим
действие небольшого элемента кольца
dr на расстоянии x
от центра:
dq=cosRd
|dE|![]() ;
;
Разложим вектор dE на dEx ,dEy и dEz
Очевидно что из-за симметрии cosсумма всехdEx и dEy будет равна нулю (левое полукольцо(заряжено противоположно правому) действует в проекциях на Ox и Oy с той же силой, но в противоположном направлении, что и правое полукольцо).
dEz=dEsin![]()
r2=x2+R2 (одинаково для всех точек кольца);
Тогда из рисунка
:
![]() ;
;
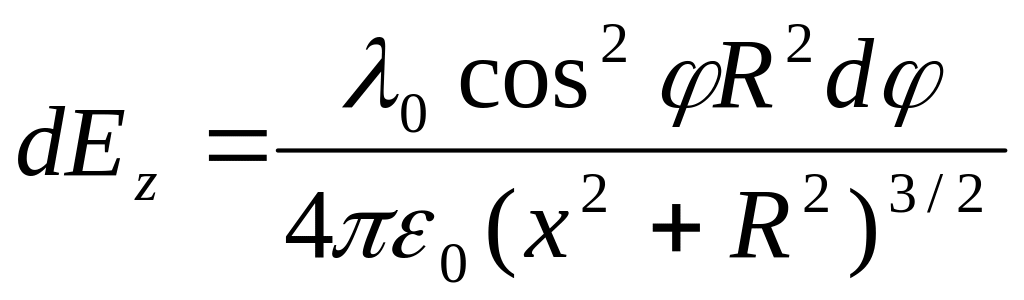 ;
;
 ;
;
Ответ:
а)
![]() ;
;
б) .
.
2.19. Длинная прямая равномерно заряженная нить имеет заряд λ на единицу длины. Найти модуль и направление электрического поля в точке, которая отстоит от нити на расстояние y и находиться на перпендикуляре к нити, проходящем через один из её концов.
Решение:

Выделили элемент dx, его заряд dq= λ*dx.
Напряжённость поля от этого элемента в точке O в проекции на Оv:
![]()
![]()
Для проекции на Ou:

И направлен под углом 450 к нити.
Ответ:

2.26 Две
скрещивающиеся, взаимно-перпендикулярные
нити бесконечной длины заряжены
равномерно с линейной плотностью
![]() .
Найти силу их взаимодействия.
.
Найти силу их взаимодействия.
Решение: copyright 2001 Андрюха, 13РФ.
Пусть наименьшее
расстояние между точками нити
![]() .
Примем координату
.
Примем координату
![]() одной из этих точек и координату
одной из этих точек и координату
![]() другой за нули. Тогда сила взаимодействия
двух элементов нитей
другой за нули. Тогда сила взаимодействия
двух элементов нитей
![]() и
и
![]() равна
равна
![]() ,
а результирующая сила взаимодействия
нитей
,
а результирующая сила взаимодействия
нитей
![]() .
.
2.30 Напряженность электрического поля E=arr, где a- постоянная, r- расстояние от центра поля. Найти плотность зарядов ρ(r), создающих это поле.
Решение:
![]()
![]()
Уравнение
Максвелла:
![]()
![]()
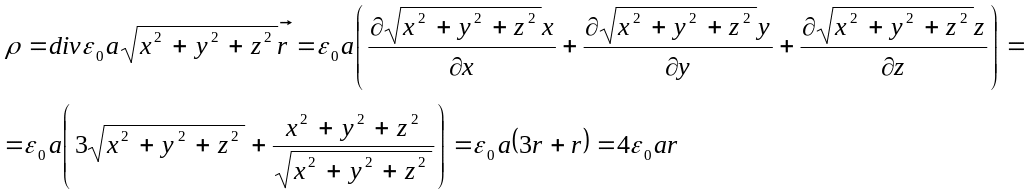 Ответ:
Ответ:
![]() .
.
2.38. Условие: Тонкое кольцо R=25 см. имеет заряд q=5,0 мкКл, неравномерно распределённый по кольцу. Найти работу электрических сил по перемещению точечного заряда q1=10ккК из центра кольца по произвольному пути в точку, находящуюся на оси кольца на l=50 см от его центра.
Решение: Работа по перемещению заряда не зависит от траектории.
A=1-2;
1=qq1/(4R0);
d2=q1dq/(40![]() );
);
2=qq1/(40 );
A==1-2=qq1(1-![]() )/(40)=0,1
Дж;
)/(40)=0,1
Дж;
Задача № 2.39 (3.32)
Находящаяся в вакууме круглая тонкая пластинка радиуса R равномерно заряжена с поверхностной плотностью . Найти потенциал и модуль напряженности электрического поля на оси пластинки как функцию расстояния l от ее центра.
Решение:
Для кольца напряженность:
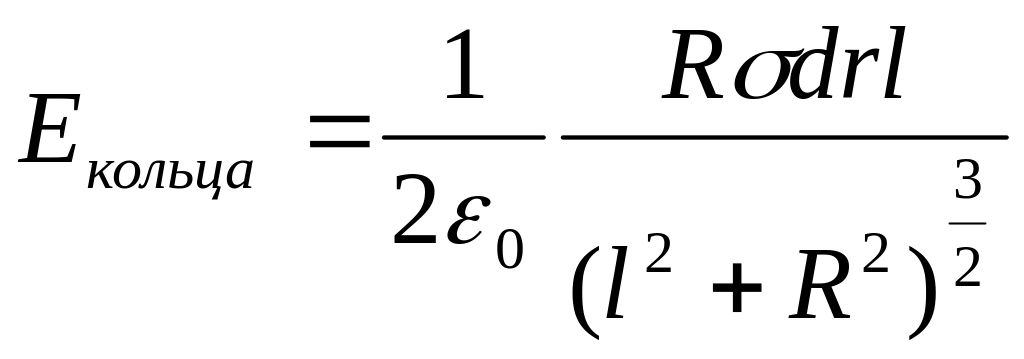 где
dr – толщина кольца;
где
dr – толщина кольца;
Разбивая диск на кольца получаем:  для
потенциала:
для
потенциала: ![]() Проинтегрируем
и получим:
Проинтегрируем
и получим:
![]()
![]() ;
;
2.40
Условие:
Коническая поверхность с основанием радиуса R и углом между боковой поверхностью и прямой соединяющей центр основания и вершину β, равномерно заряжена с поверхностной плотностью . Найти потенциал в вершине конуса.
Решение:
Рассмотрим точечный заряд q, находящийся на расстоянии r от вершины конуса. Создаваемый им потенциал равен:
![]()
Просуммируем потенциалы, создаваемые элементарными кольцами по всему конусу:
![]()

Ответ:
![]()
№ 2.51.
2.51.
Два коаксиальных кольца, каждое радиуса R, из тонкой проволоки находятся на малом расстоянии l друг от друга (l<<R) и имеют заряды q и –q. Найти потенциал и напряженность электрического поля на оси системы как функции координаты х.
РЕШЕНИЕ:
Найдем зависимость потенциала системы от расстояния.
В ыразим
через полученное значение напряженность.
ыразим
через полученное значение напряженность.
О ТВЕТ.
ТВЕТ.

2.58 Потенциал
поля внутри заряженного шара зависит
только от расстояния до его центра как
![]() ,
где
,
где
![]() и
и
![]() - постоянные. Найти распределение
объёмного заряда
- постоянные. Найти распределение
объёмного заряда
![]() внутри шара.
внутри шара.
Решение: copyright 2001 Андрюха, 13РФ.
![]() .
Возьмём две концентрические сферы
радиусами
.
Возьмём две концентрические сферы
радиусами
![]() и
и
![]() .
Тогда между ними заключен заряд
.
Тогда между ними заключен заряд
![]() .
По теореме Гаусса
.
По теореме Гаусса![]() .Приравнивая,
получаем
.Приравнивая,
получаем![]() .
.
2.64
Точечный заряд q находиться между двумя проводящими взаимно перпендикулярными полуплоскостями. Расстояние от заряда до каждой полуплоскости l. Найти модуль силы, действующей на заряд.
Решение:
Полуплоскости равносильны трём точечным зарядам, которые находятся в вершинах квадрата со стороной 2l, в четвертой вершине – заряд из условия. Знаки и значения зарядов на диагоналях совпадают и противоположны другой диагонали. По закону Кулона:
![]()
Ответ:
![]()
2.64
Точечный заряд q находиться между двумя проводящими взаимно перпендикулярными полуплоскостями. Расстояние от заряда до каждой полуплоскости l. Найти модуль силы, действующей на заряд.
Решение:
Полуплоскости равносильны трём точечным зарядам, которые находятся в вершинах квадрата со стороной 2l, в четвертой вершине – заряд из условия. Знаки и значения зарядов на диагоналях совпадают и противоположны другой диагонали. По закону Кулона:
Ответ:
№ 2.66.
Точечный заряд q находится на расстоянии l от проводящей безграничной плоскости. Определить поверхностную плотность зарядов, индуцированных на плоскости, как функцию расстояния r от основания перпендикуляра, опущенного из заряда на плоскость.
РЕШЕНИЕ.
Так как плоскость проводящая, можем записать.

![]()
ОТВЕТ:
![]() .
.
№2.68.
Условие:
На расстоянии l от плоскости из диэлектрика перпендикулярно ей расположена равномерно заряженная нить с линейной плотностью заряда . Найти поверхностную плотность заряда на плоскости на расстоянии r от точки проекции нити на плоскость и в точке проекции.
Решение: рассмотрим срез ( т. к. поле симметрично относительно нити)


При рассмотрении создаваемого на достаточно маленьком расстоянии от поверхности плоскости поля можно пренебречь его параллельной компонентой, а рассмотреть лишь перпендикулярную компоненту, рассчитываемую по формуле:
![]() ,
тогда имеем:
,
тогда имеем:
![]() ,
тогда
,
тогда
![]()
№2.71
Заряд q распределен неравномерно по тонкому кольцу радиуса R. На расстоянии l от центра кольца на его оси расположен центр проводящей незаряженной сферы. Найти её потенциал.
Решение:
![]() ,
(внутри сферы потенциал постоянен)
,
(внутри сферы потенциал постоянен)
№-2.074.
4 большие металлические пластины расположены на малом расстоянии d друг от друга.
Внешние пластины
соеденены проводником , а на внутренние
подана разность потенциалов
![]() .
Найти: а)напряжённость
электрического поля между пластинами;
.
Найти: а)напряжённость
электрического поля между пластинами;
б)суммарный заряд на единицу площади каждой пластины.
Решение:


1
По определению :
![]()
2 Эту систему можно рассмотреть как систему 3-х конденсаторов
3
одинаковых ёмкостей. Два из них соеденены последовательно ,а 3-й
4
параллельно
им. Следовательно напряжение на каждом
из 2-х соедененых последовательно
конденсаторах напряжение будет равно
![]() ;
;
![]() ;
;
Исходя
из тех же соображений можно записать:![]()
![]() ;
;
Можно
также записать
![]() ;
Отсюда находим :
;
Отсюда находим :
![]() а
а
![]() ;
;
![]() и
и
![]()
![]()
![]() ;
;
![]()
![]() ;
;
Ответ: ;
![]() ;
.
;
.
![]()
2.77. Найти электрическую силу, которую испытывает заряд, приходящийся на единицу поверхности произвольного проводника в точке, где = 46 мкКл/м2.
Решение:

Примечание: в данной задаче используется модель, в которой полагается, что поле у поверхности проводника такое же, как у поверхности заряженной плоскости.
Ответ:![]()
№2.79
Условие задачи:
Незаряженный
проводящий шар радиуса r
поместили в однородное поле, в результате
чего на поверхности шара появился
индуцированный заряд с поверхностной
плотностью
![]() ,
где
- полярный угол. Найти модуль суммарной
электрической силы, действующей на весь
индуцированный заряд одного знака.
,
где
- полярный угол. Найти модуль суммарной
электрической силы, действующей на весь
индуцированный заряд одного знака.

Рисунок:
Решение:
Найдем суммарный заряд одного знака, проинтегрировав по половине поверхности:
![]()
Найдем силу, действующую на весь индуцированный заряд одного знака:
F=Eq= ,
,
где Ф-поток вектора напряженности э/ст. поля через половину поверхности шара
Ответ:
F=
№ 2.80
Найти энергию упругого диполя с поляризованностью p=Eво внешнем электрическом поле с напряженностью E .
Решение:
M=[pE] однако , так как при повороте диполя относительно E диполь удлиняется или сжимается, т.е. плечо силы изменяется, то M не постоянен.
M=[ElE] , El - вектор проекции поля на диполь El=Ecos
