Бесконечно большая функция

Расстановка ударений: БЕСКОНЕ`ЧНО БОЛЬША`Я ФУ`НКЦИЯ

БЕСКОНЕЧНО БОЛЬШАЯ ФУНКЦИЯ - функция переменного х, к-рая в данном процессе изменения х становится и остается по абсолютной величине больше любого наперед заданного числа. Точнее, функция f(x), определенная в окрестности точки х₀, наз. бесконечно большой функцией при х, стремящемся к x₀, если для любого числа М > 0 найдется такое число δ = δ (М) > 0, что для всех х ≠ х₀ и таких, что |х - х₀ | < δ, выполняется неравенство |f(x)| > M. Этот факт записывается так:

Аналогичным образом определяются

Напр.,

означает, что для любого М > 0 найдется такое δ = δ (M) > 0, что для всех z < - δ выполняется неравенство f(x) > M. Изучение Б. б. ф. может быть сведено к изучению бесконечно малых функций, т. к. если f(x) есть Б. б. ф., то функция ψ (х) = 1/f(x) является бесконечно малой.

Связь между бесконечно малыми и бесконечно большими функциями

Если f(x) — бесконечно большая функция при x → x0, то  

1

f(x)

   — бесконечно малая функция при x → x0.

Если α(x) — бесконечно малая функция при x → x0   и   "x О 

·

O

(x0)    α(x) ≠ 0,   то   

1

α(x)

   — бесконечно большая функция при x → x0.

Вопрос №14

Непрерывность функции на отрезке

Наряду с непрерывностью функции в точке рассматривают ее непрерывность на разных промежутках.

Функция f(x) называется непрерывной на интервале (a, b), если она непрерывна в каждой точке этого интервала.

Функция f(x) называется непрерывной на отрезке [a, b], если она непрерывна на интервале (a, b), непрерывна справа в точке a и непрерывна слева в точке b.

Замечание. Функция, непрерывная на отрезке [a,b] может быть разрывной в точках a и b (рис. 1)

Множество функций, непрерывных на отрезке [a, b] обозначается символом C[a, b].

Свойства функций, непрерывных на отрезке

Теорема 1 (об ограниченности непрерывной функции). Если функция f(x) непрерывна на отрезке [a, b], то она ограничена на этом отрезке, т.е. существует такое число C> 0, что "x О [a, b] выполняется неравенство |f(x)| ≤ C.

Теорема 2 (Вейерштрасс). Если функция f(x) непрерывна на отрезке [a, b], то она достигает на этом отрезке своего наибольшего значения M и наименьшего значения m, т.е. существуют точки α, β О [a, b] такие, что m = f(α) ≤ f(x) ≤ f(β) = M для всех x О [a, b] (рис.2).

Наибольшее значение M обозначается символом max_{x О [a, b]} f(x), а наименьшее значение m — символом min_{x О [a, b]} f(x).

Теорема 3 (о существовании нуля). Если функция f(x) непрерывна на отрезке [a, b] и на концах отрезка принимает ненулевые значения разных знаков, то на интервале (a, b) найдется по крайней мере одна точка ξ в которой f(ξ) = 0.

Геометрический смысл теоремы состоит в том, что график функции, удовлетворяющей условиям теоремы, обязательно пересечет ось OX (рис.3).

Замечание. На этой теореме основан метод приближенного решения уравнения

 

f(x) = 0,

(1)

 

называемый методом бисекции (дихотомии), или методом половинного деления.

Схема решения уравнения методом половинного деления

Отделяем корни уравнения (1). Для этого устанавливаем промежутки, в которых функция f(x) имеет единственный нуль и на его концах принимает значения разных знаков. С этой целью используем графические построения или составляем таблицу значений функции. Обозначим такой отрезок символом σ₀.

Разделим этот отрезок пополам. Если в середине отрезка функция f(x) равна нулю, уравнение (1) решено. В противном случае на концах одного из полученных половинных отрезков f(x) вновь принимает значения разных знаков. Обозначим этот отрезок символом σ₁ и вновь разделим его пополам. Если в середине σ₁ функция f(x) равна нулю, то уравнение (1) решено. В противном случае продолжим указанную процедуру. Таким образом, мы либо на каком–то этапе получим точку, в которой f(x) = 0, т.е. точное решение уравнения (1), либо получим последовательность вложенных друг в друга отрезков σ₀ Й σ₁ Й … , на каждом из которых f(x) имеет значения разных знаков. В этом случае можно заключить искомый корень уравнения (1) в промежуток произвольной длины и, следовательно, вычислить этот корень с любой заданной точностью.

Замечание. Метод неприменим для отыскания корней четной кратности.

Теорема 4 (Больцано–Коши). Если функция f(x) непрерывна на отрезке [a, b], то она принимает на (a,b) все промежуточные значения между f(a) и f(b).

Доказательства теорем приведены в книге Л.Д. Кудрявцева “Краткий курс математического анализа”. Т.1. М.: ФИЗМАТЛИТ, 2002. Стр.122–124.

Cуществование непрерывной обратной функции

Пусть функция y = f(x) определена, строго монотонна и непрерывна на отрезке [a,b]. Тогда на отрезке [α, β] ( α = f(a), β = f(b) ) cуществует обратная функция x =g(y), также строго монотонная и непрерывная на отрезке (α, β).

Вопрос №15

Точки, в которых функция не обладает свойством непрерывности, называется точкой разрыва.

1. Устранимый разрыв

Точка a называется точкой устранимого разрыва функции, если предел точки a существует, но в самой точке a значения не существует.

2) Разрыв 1 рода.

Тока а называется разрывом 1 рода если пределы справа и слева конечны и не равны друг другу.

3) разрыв 2 рода.

Точка a называется точкой разрыва 2 рода, если в этой точке функция не имеет хотя бы одного одностороннего предела, либо хотя бы один односторонний предел равен бесконечности.

Вопрос №16

Приращение аргумента Δx = x –x0

Приращение функции Δf = f (x0 + Δx) – f (x0)

Производной функции в данной фиксированной точке при дельта X стремящемся к 0, называется предел приращения функции дельта Y к приращению аргумента дельта X, если этот предел существует.

Геометрический смысл производной. Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.

Касательная к графику функции в точке М (х0, у0):

У-У0=К(Х-Х0)

Определение непрерывности в терминах приращений аргумента и функции

Определение непрерывности можно также сформулировать, используя приращения аргумента и функции. Функция является непрерывной в точке x = a, если справедливо равенство

где  .  Приведенные определения непрерывности функции эквивалентны на множестве действительных чисел.  Функция является непрерывной на данном интервале, если она непрерывна в каждой точке этого интервала. 

Связь между непрерывностью и дифференцируемостью функции. Если функция  f ( x ) дифференцируема в некоторой точке, то она непрерывна в этой точке. Обратное неверно:  непрерывная функция может не иметь производной.  

С л е д с т в и е . Если функция разрывна в некоторой точке, то она не имеет производной в этой точке.

П р и м е р .

Функция  y = | x | ( рис.3 )  всюду непрерывна, но она не имеет производной при  x = 0 , так как в этой точке не существует касательной к графику этой функции. ( Подумайте, почему ? )

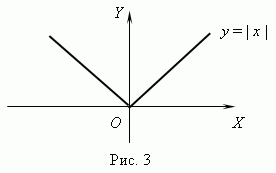
Достаточные признаки монотонности функции.

Если  f ’( x ) > 0  в каждой точке интервала ( a, b ), то функция  f ( x ) возрастает на этом интервале.

Если  f ’( x ) < 0  в каждой точке интервала ( a, b ) , то функция  f ( x ) убывает на этом интервале.

Бескочная производная

Можно ввести также понятие бесконечной производной f (x)=+ f (x)=− f (x)=   (последний случай может иметь место, если, например, lim x +0 x y=+ lim x −0 x y=− .

Если функция дифференцируема в точке x 0, то она непрерывна в этой точке.

Односторонние производные

Односторонние производные функции в точке.

  Определение. Правой (левой) производной функции f(x) в точке х = х₀ называется правое (левое) значение предела отношения   при условии, что это отношение существует.

 

 

  Если функция f(x) имеет производную в некоторой точке х = х₀, то она имеет в этой точке односторонние производные. Однако, обратное утверждение неверно. Во- первых функция может иметь разрыв в точке х₀, а во- вторых, даже если функция непрерывна в точке х₀, она может быть в ней не дифференцируема.

 

  Например: f(x) = x- имеет в точке х = 0 и левую и правую производную, непрерывна  в этой точке, однако, не имеет в ней производной.

  Теорема. (Необходимое условие существования производной) Если функция f(x) имеет производную в точке х₀, то она непрерывна в этой точке.

  Понятно, что это условие не является достаточным.

Вопрос №17