
- •1(X1;y1;z1) - произвольная точкаплоскости) на направление нормального вектора
- •1). Скалярное произведение подчиняется закону коммутативности:
- •2). Скалярное произведение двух векторов равно нулю тогда и только тогда, когда хотя бы один из векторов нулевой или векторы ортогональны:
- •1) Коллинеарны;
- •2) Одинаково направлены (сонаправлены —);
- •3) Имеют равные модули.
- •1. Собственные векторы и собственные значения линейного оператора.
- •2. Условие диагональности линейного оператора.
- •1) Если , то плоскости совпадают;
- •2) Если , то плоскости параллельны;
- •3) Если или , то плоскости пересекаются и система уравнений
- •Проходящей через две данные точки
- •Прямая как пересечение двух плоскостей
- •Взаимное расположение двух прямых в пространстве
1) Если , то плоскости совпадают;
2) Если , то плоскости параллельны;
3) Если или , то плоскости пересекаются и система уравнений
является уравнениями прямой пересечения данных плоскостей.
Различные способы задания прямых
К аноническое
уравнение прямой
аноническое
уравнение прямой
![]() ,
,
где (х0; у0; z0) – точка прямой,
![]() (k;
l;
m)
– направляющий вектор.
(k;
l;
m)
– направляющий вектор.
Уравнение прямой в пространстве,
Проходящей через две данные точки
![]()
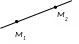
Прямая как пересечение двух плоскостей
![]()

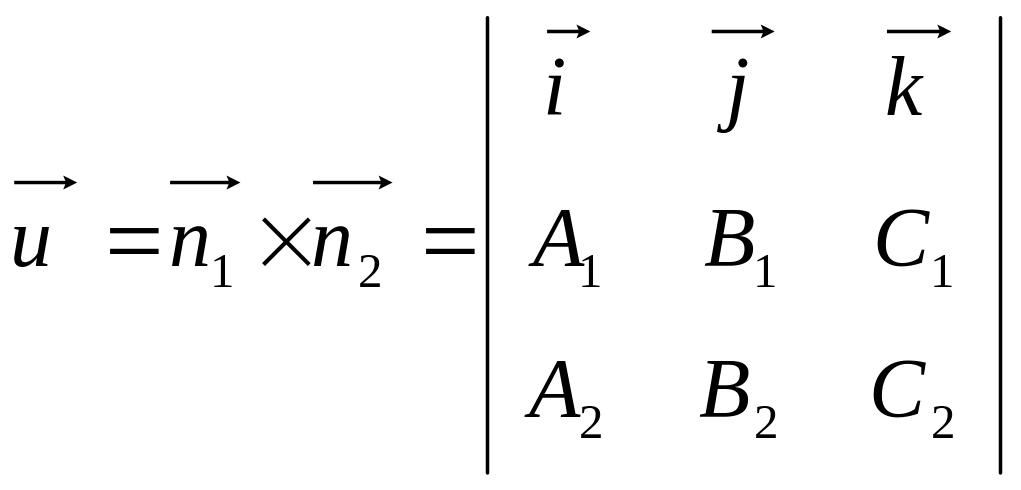 ,
,
где – направляющий вектор прямой,
![]() и
и
![]() – векторы нормалей данных плоскостей.
– векторы нормалей данных плоскостей.
№21.2
Взаимное расположение двух прямых в пространстве
l1: ![]() ; l2:
; l2: ![]()


![]() и при этом
и при этом
(!) ![]()
прямые параллельны и при этом различны
 и при этом
и при этом
(!) ![]()
прямые совпадают

![]() – некомпланарные
векторы, т.е.
– некомпланарные
векторы, т.е.
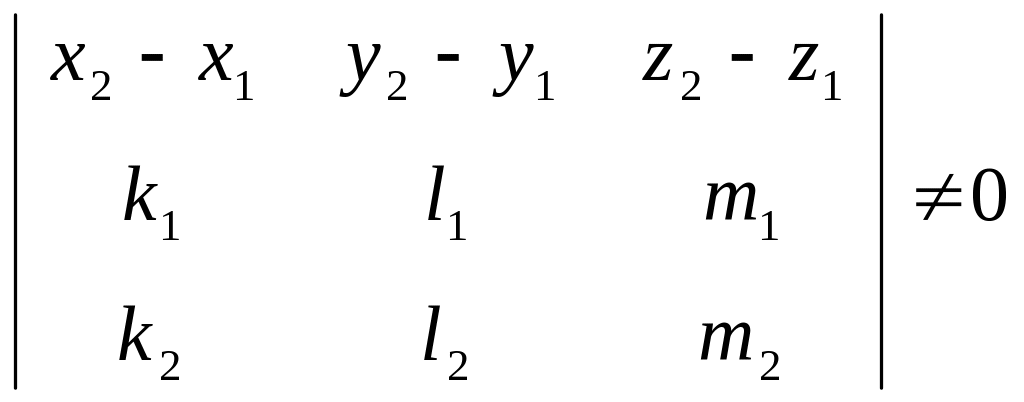
прямые скрещиваются
– компланарные векторы, т.е.

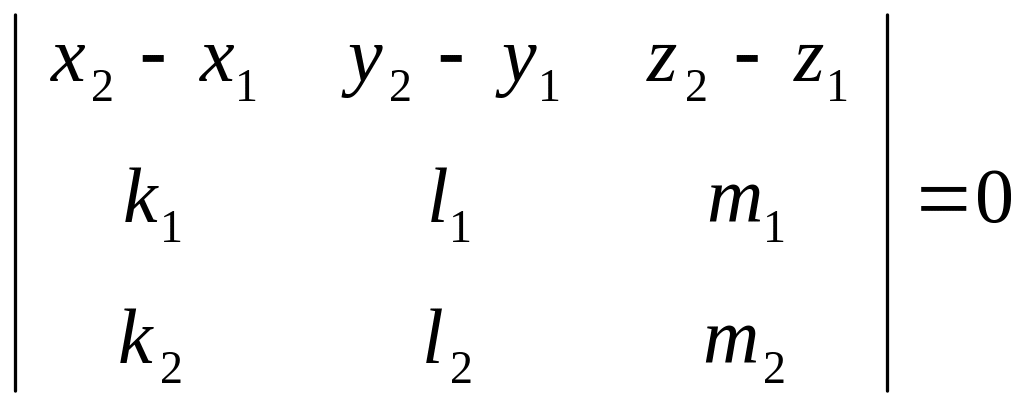 и
при этом
и
при этом
прямые пересекаются (!) ![]() –
неколлинеарны,
т.е.
–
неколлинеарны,
т.е.
нарушается одно из равенств:
№22
Обратная матрица - такая матрица, при умножении на которую исходная матрица даёт в результате единичную матрицу E. Обратную матрицу можно найти только у квадратной матрицы, тоесть у матрицы, у которой число строк равняется числу столбцов.
Обра́тная
ма́трица — такая матрица A−1,
при умножении на которую исходная
матрица A
даёт в результате единичную матрицу E:
![]()
Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.
Определение
Пусть
![]() — прямоугольная матрица.
— прямоугольная матрица.
Тогда по определению рангом матрицы A является:
ноль, если A — нулевая матрица;
число
![]() , где Mr
— минор матрицы A
порядка r,
а Mr
+ 1 — окаймляющий к нему минор порядка
(r
+ 1), если они существуют.
, где Mr
— минор матрицы A
порядка r,
а Mr
+ 1 — окаймляющий к нему минор порядка
(r
+ 1), если они существуют.
Теорема
(о корректности определения рангов).
Пусть все миноры матрицы
порядка k
равны нулю (Mk
= 0). Тогда
![]() ,
если они существуют.
,
если они существуют.
Линейное преобразование и ранг матрицы
Пусть
A
— матрица размера
![]() над полем C
(или R).
Пусть T
— линейное преобразование, соответствующее
A
в стандартном базисе; это значит, что
T(x)
= Ax.
Ранг матрицы A
— это размерность области значений
преобразования T.
над полем C
(или R).
Пусть T
— линейное преобразование, соответствующее
A
в стандартном базисе; это значит, что
T(x)
= Ax.
Ранг матрицы A
— это размерность области значений
преобразования T.
Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.
Элементарные преобразования используются в методе Гаусса для приведения матрицы к треугольному или ступенчатому виду.
№23
Линейная независимость векторов
V- произвольные векторное пространство. Система векторов u1……un пространства V линейно независима, если существуют такие числа α1 u1+ α2 u2+….+ αnun=0 выполняется при αi =0
Базис- множество таких векторов в векторном пространстве , что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества.
Размерность линейного пространства:
Х- n-мерное линейное пространство, если существует натуральное n такое, что х содержит линейно независимую систему из n векторов , а любая система из n+1 – зависима.
№24
Линейное (векторное) пространство — естественное обобщение обычного трёхмерного евклидова пространства; в нём определены две алгебраические операции: сложение элементов (векторов) и умножение элементов на число (скаляр), подчинённые семи аксиомам.
Определение
Пусть
![]() — поле вещественных или комплексных
чисел (поле скаляров). Множество
— поле вещественных или комплексных
чисел (поле скаляров). Множество
![]() называется линейным (векторным)
пространством над
,
если для каждых двух его элементов x и
y определена их сумма
называется линейным (векторным)
пространством над
,
если для каждых двух его элементов x и
y определена их сумма
![]() и для любого элемента
и для любого элемента
![]() и
числа
и
числа
![]() определено произведение
определено произведение
![]()
причём эти операции удовлетворяют следующим аксиомам.
Аксиомы линейного пространства
(x + y) + z = x + (y + z) (ассоциативность сложения);
x + y = y + x (коммутативность сложения);
(λμ)x = λ(μx) (ассоциативность умножения);
(λ + μ)x = λx + μx (дистрибутивность);
λ(x + y) = λx + λy (дистрибутивность);
в
существует такой элемент
![]() ,
что
,
что
![]() для любого
(нулевой элемент);
для любого
(нулевой элемент);
![]() (умножение на
единицу);
(умножение на
единицу);
Если
в множестве
введены операции сложения и умножения
на число так, что
превращено в линейное пространство, то
говорят, что
наделено линейной структурой. Линейное
пространство над
![]() называется вещественным, а над
называется вещественным, а над
![]() — комплексным линейным пространством.
— комплексным линейным пространством.
КРИТЕРИЙ ЛИНЕЙНОЙ ЗАВИСИМОСТИ СИСТЕМЫ ВЕКТОРОВ ЛИНЕЙНОГО ПРОСТРАНСТВА
Для того, чтобы система векторов линейного пространства была линейно зависма, необходимо и достаточно, чтобы хотя бы один из векторов системы линейно выражался через остальные векторы системы (мог быть представлен в виде разложения по векторам системы).
№25.1
Поверхности второго порядка
К невырожденным поверхностям второго порядка относятся эллипсоид, эллиптический параболоид, гиперболический параболоид, однополостной гиперболоид и двуполостной гиперболоид. Строгое изучение этих поверхностей проводится в курсе аналитической геометрии. Здесь же мы ограничимся определениями и иллюстрациями.
Определение
Поверхность, задаваемая в некоторой
прямоугольной декартовой системе
координат уравнением
![]() a > 0, b > 0, c > 0, называется эллипсоидом.
a > 0, b > 0, c > 0, называется эллипсоидом.
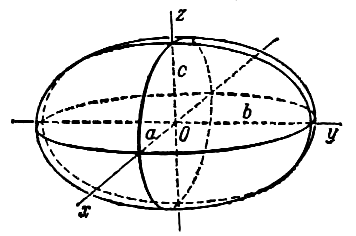
Свойства эллипсоида.
Эллипсоид
– ограниченная поверхность, поскольку
из его уравнения следует, что
![]()
![]()
![]()
Эллипсоид обладает
центральной симметрией относительно начала координат,
осевой симметрией относительно координатных осей,
плоскостной симметрией относительно начала координат.
В сечении эллипсоида плоскостью, перпендикулярной любой из координатных осей, получается эллипс.
Определение
Поверхность,
задаваемая в некоторой прямоугольной
декартовой системе координат уравнением
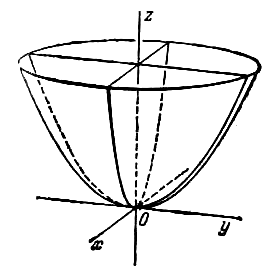
![]() a
> 0, b > 0, называется эллиптическим
параболоидом.
a
> 0, b > 0, называется эллиптическим
параболоидом.
Свойства эллиптического параболоида.
Эллиптический параболоид – неограниченная поверхность, поскольку из его уравнения следует, что z ≥ 0 и принимает сколь угодно большие значения.
Эллиптический параболоид обладает
осевой симметрией относительно оси Oz,
плоскостной симметрией относительно координатных осей Oxz и Oyz.
В сечении эллиптического параболоида плоскостью, ортогональной оси Oz, получается эллипс, а плоскостями, ортогональными осям Ox и Oy – парабола.
Определение
Поверхность,
задаваемая в некоторой прямоугольной
декартовой системе координат уравнением
![]() a > 0, b > 0, называется гиперболическим
параболоидом.
a > 0, b > 0, называется гиперболическим
параболоидом.
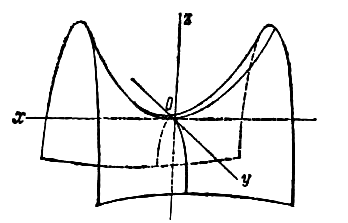
Свойства гиперболического параболоида.
№25.2
Гиперболический параболоид – неограниченная поверхность, поскольку из его уравнения следует, что z – любое число.
Гиперболический параболоид обладает
осевой симметрией относительно оси Oz,
плоскостной симметрией относительно координатных плоскостей Oxz и Oyz.
В сечении гиперболического параболоида плоскостью, ортогональной оси координат Oz, получается гипербола, а плоскостями, ортогональными осям Ox и Oy, – парабола.
Гиперболический параболоид может быть получен поступательным перемещением в пространстве параболы так, что ее вершина перемещается вдоль другой параболы, ось которой параллельна оси первой параболы, а ветви направлены противоположно, причем их плоскости взаимно перпендикулярны.
Определение
Поверхность,
задаваемая в некоторой прямоугольной
декартовой системе координат уравнением
![]() a > 0, b > 0, c > 0, называется однополостным
гиперболоидом.
a > 0, b > 0, c > 0, называется однополостным
гиперболоидом.
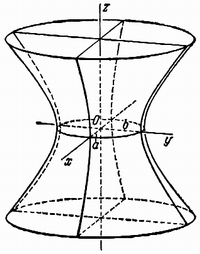
Свойства однополостного гиперболоида.
Однополостной гиперболоид – неограниченная поверхность, поскольку из его уравнения следует, что z – любое число.
Однополостной гиперболоид обладает
центральной симметрией относительно начала координат,
осевой симметрией относительно всех координатных осей,
плоскостной симметрией относительно всех координатных плоскостей.
В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат Oz, получается эллипс, а плоскостями, ортогональными осям Ox и Oy – гипербола.
Определение
Поверхность,
задаваемая в некоторой прямоугольной
декартовой системе координат уравнением
![]() a > 0, b > 0, c > 0, называется двуполостным
гиперболоидом.
a > 0, b > 0, c > 0, называется двуполостным
гиперболоидом.
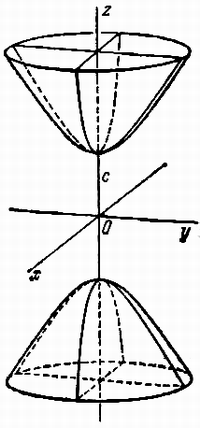
Свойства двуполостного гиперболоида.
Двуполостный
гиперболоид – неограниченная поверхность,
поскольку из его уравнения следует, что
![]() и неограничен сверху.
и неограничен сверху.
Двуполостный гиперболоид обладает
центральной симметрией относительно начала координат,
осевой симметрией относительно всех координатных осей,
плоскостной симметрией относительно всех координатных плоскостей.
№25.3
В
сечении однополостного гиперболоида
плоскостью, перпендикулярной оси
координат Oz, при
![]() получается
эллипс, при
получается
эллипс, при
![]() – точка, а в сечении плоскостями,
перпендикулярными осям Ox и Oy, – гипербола.
– точка, а в сечении плоскостями,
перпендикулярными осям Ox и Oy, – гипербола.
По аналогии с коническими сечениями существуют и вырожденные поверхности второго порядка. Так, уравнением второго порядка x2 = 0 описывается пара совпадающих плоскостей, уравнением x2 = 1 – пара параллельных плоскостей, уравнением x2 – y2 = 0 – пара пересекающихся плоскостей. Уравнение x2 + y2 + z2 = 0 описывает точку с координатами (0; 0; 0), уравнение x2 + y2 = 1 – круговой цилиндр, уравнение x2 + y2 = z2 – круговой конус. Существуют и другие вырожденные случаи. Полная теория поверхностей второго порядка рассматривается в курсе аналитической геометрии.
