5)Равносильность формул.
Равносильные формулы логики предикатов.
Определение 1.
Две формулы логики предикатов А и В называются равносильными на области М, если они принимают одинаковые логические значения при всех значениях входящих в них переменных, отнесенных к области М.
Определение 2.
Две формулы логики предикатов А и В называются равносильными, если они равносильны на всякой области.
Ясно, что все равносильности алгебры высказываний будут верны, если в них вместо переменных высказываний подставить формулы логики предикатов. Но, кроме того, имеют место равносильности самой логики предикатов. Рассмотрим основные из этих равносильностей.
Пусть А(х) и В(х) – переменные предикаты, а С – переменное высказывание (или формула, не содержащая х). Тогда имеют место равносильности:
1.
2.
3.
4.
5.
.
Равносильность
1 означает тот простой факт, что, если
не для всех х истинно А(х), то существует
х, при котором будет истиной
.
Равносильность 2 означает тот простой факт, что, если не существует х, при котором истинно А(х), то для всех х будет истиной .
Равносильности 3 и 4 получаются из равносильностей 1 и 2, соответственно, если от обеих их частей взять отрицания и воспользоваться законом двойного отрицания.
ЗАКОНЫ ЛОГИЧЕСКИХ ОПЕРАЦИЙ.
(общезначимые формулы логики предикатов)
|
|
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
6) Основные равносильности, содержащие кванторы.
1. Законы де Моргана ¬(∀xP(x))=∃x¬(P(x)) ¬(∃xP(x))=∀x¬(P(x)) 2. Коммутативность ∀x∀yP(x,y)=∀y∀xP(x,y) ∃x∃yP(x,y)=∃y∃xP(x,y) 3. Дистрибутивность ∀x(P(x)&Q(x))=∀xP(x)&∀xQ(x) ∃x(P(x)&Q(x))=∃xP(x)&∃xQ(x) 4. Ограничение действия кванторов ∀x(P(x)vQ(y))=∀xP(x)vQ(y) ∃x(P(x)&Q(y))=∃xP(x)&Q(y) 5. Для любого двухместного предиката ∃y∀xP(x,y)→∀x∃yP(x,y)=1
7)Применение кванторов для записи математических определение и теорем.
Алгебра множеств
1)Множество.
Под множеством понимают совокупность объектов (предметов или понятий), которая рассматривается как одно целое. Элементом множества называется объект, входящий в состав множества.
Под универсумом (U или I ) понимают множество, включающее в себя все множества в данном контексте.
2)Равенство множеств.
Два
множества А и В называются равными (А=В)
тогда и только тогда, когда определяющие
их предикаты равносильны
3)Операции над множествами и их свойства.
Любой одномерный предикат Р(х), определенный на I можно считать предикатом, порожденный множеством.
Булевы операции над множествами.
Дополнением
ко множеству
А относительно универсального множества
I
называется множество, обозначаемое
,
определяемое следующим:
Объединением
множеств А и
В называется множество обозначаемое
А
B,
определяемое следующим:
Пересечением
множеств А и В называется множество,
обозначаемое А
В,
определяемое следующим:
Разностью
множеств А и В называется множество,
обозначаемое А\В, определяемое следующей
равносильностью:
.
Так же имеет место равенство А\В=А
Симметрической
разностью
множеств А и В называют множество,
обозначаемое А
В,
определяемое следующим:
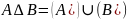
4)Геометрическая интерпретация операций над множествами («круги Эйлера или «диаграммы Венка»).
5)Формула включения исключения.
1)
2)
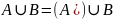
6) Подмножество.
Множество
А является подмножеством В (пишут А(с)В)
тогда и только тогда когда каждый элемент
множества А является элементом множества
В, т.е А(с)В
Для
того что бы множество А являлось
подмножеством множества В необходимо
и достаточно что бы А\В=
7)Свойства подмножеств.
1. А(с) - рефлексивность
2. (А(с)В)&(В(с)С)=> А(с)С –транзитивность
3. (А(с) В) & (В(с)А) А=В -антисимметричность
8)Декартово произведения множеств.
Декартовым
произведением множеств Х
и Y
называется множество, обозначаемое Х
Y,
элементами которого являются упорядоченные
пары (x;y),
где
.
Равенство упорядоченных пар z1=(x1,y1)
и z2=(x2,y2)
(z1,z2
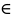X
Y)
понимается в следующем смысле: z1=z2
9)Множество-степень.
Множество подмножеств данного множества называется множество-степень.
А={а,в,с}
2^А={∅,{а},{в},{с},{а,в},{а,с},{в,с},{а,в,с}}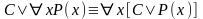