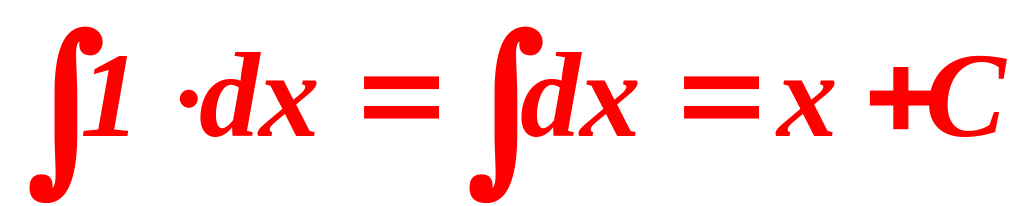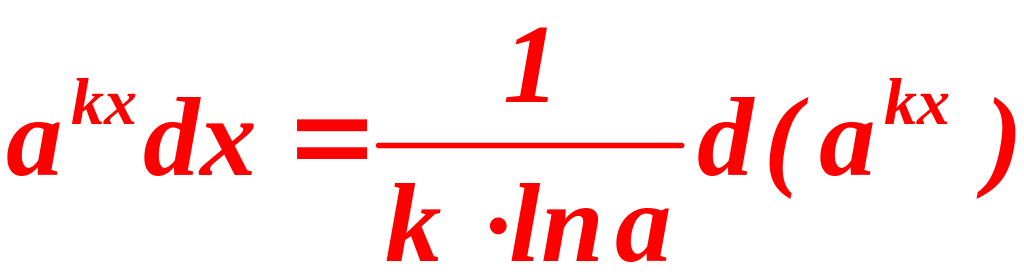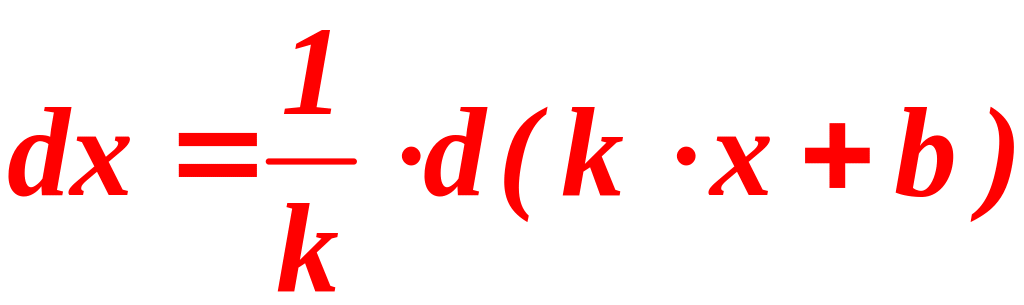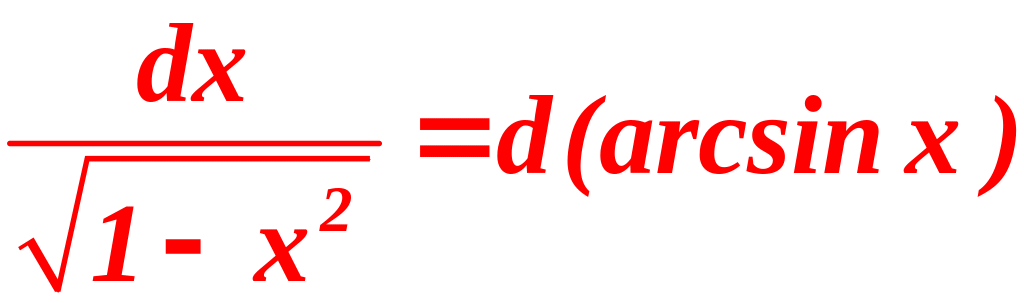- •1.2. Понятие неопределенного интеграла и его свойства
- •Свойства неопределенного интеграла
- •1.3. Правила и формулы интегрирования Правила:
- •2. Замена переменной в неопределенном интеграле
- •Алгоритм интегрирования методом замены переменной.
- •3. Интегрирование «по частям» в неопределенном интеграле
- •- Формула интегрирования по частям.
- •Алгоритм нахождения интеграла методом интегрирования по частям.
- •4. Интегрирование выражений, содержащих квадратный трехчлен
- •Интегралы вида ,
- •5. Простейшие рациональные дроби и их интегрирование
- •Интегрирование рациональных дробей
- •6. Интегрирование некоторых иррациональных выражений
- •7. Интегрирование тригонометрических функций
- •8. Определенный интеграл
- •8.1. Понятие определенного интеграла.
- •8.2. Геометрический смысл определенного интеграла
- •8.3. Свойства определенного интеграла
- •8.4. Интеграл как функция переменного верхнего предела
- •8.5. Производная от интеграла по переменному верхнему пределу.
- •8.6. Вычисление определенного интеграла. Формула Ньютона-Лейбница
- •8.7. Замена переменной в определенном интеграле
- •8.8. Интеграл с симметричными пределами от четной и нечетной функции
- •8. 9. Интегрирование «по частям» в определенном интеграле
- •4. Длина дуги кривой и ее дифференциал.
- •Задача о вычислении пути.
- •12. Несобственные интегралы
- •12.1. Несобственные интегралы с бесконечными пределами
- •12.2. Применение формулы Ньютона-Лейбница.
- •12.3. Несобственные интегралы с конечными пределами
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ
ОДНОЙ ПЕРЕМЕННОЙ
1. Неопределенный интеграл
Пусть
![]() определена и дифференцируема на множестве
определена и дифференцируема на множестве
![]() ,
т.е. мы знаем, как найти производную этой
функции. Например, известен закон
движения материальной точки
,
т.е. мы знаем, как найти производную этой
функции. Например, известен закон
движения материальной точки
![]() ,
то путем дифференцирования мы можем
найти
,
то путем дифференцирования мы можем
найти
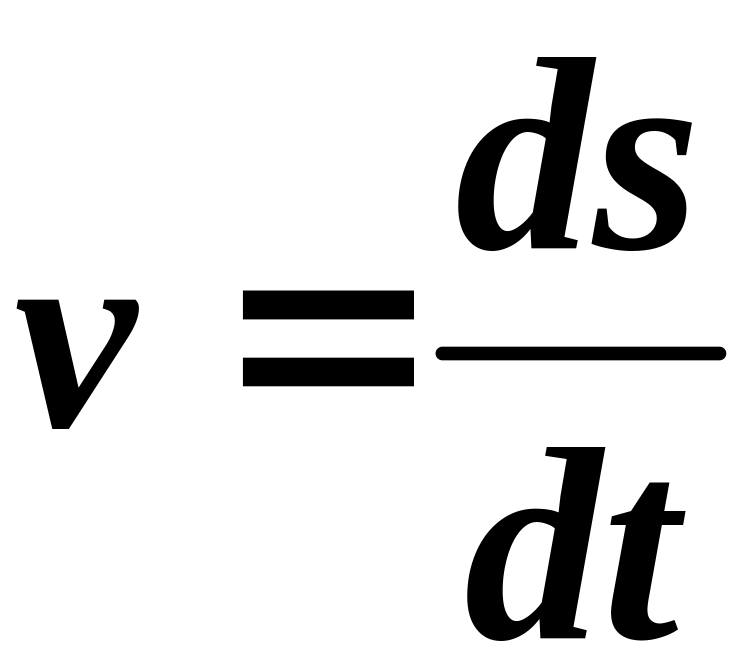 и
и
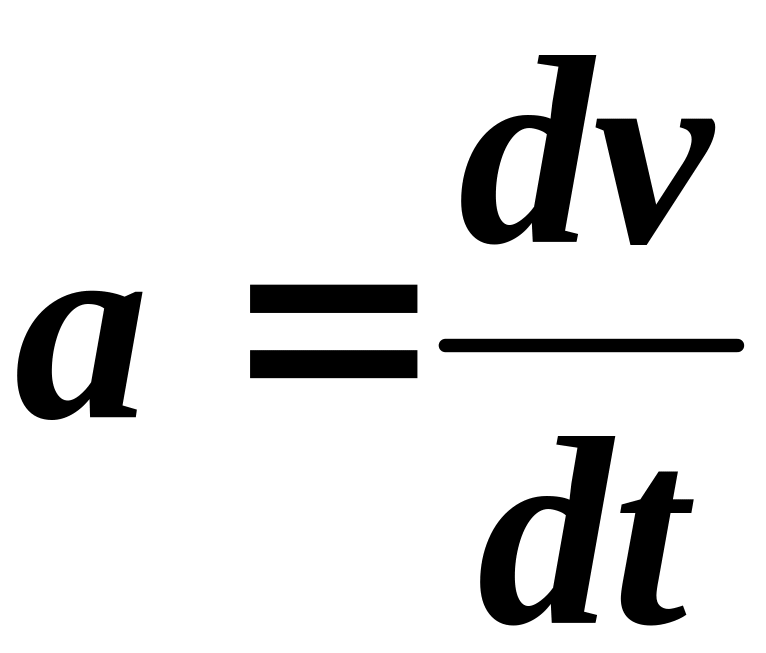 .
.
![]()
1.1. Понятие первообразной функции
Пусть
![]() определена на
определена на
![]() .
.
Определение:
Функция
![]() называется первообразной функцией для
функции
называется первообразной функцией для
функции![]() ,
если
,
если
![]() .
.
Пример.
1)
 -
первообразная для
-
первообразная для
![]() ,
т.к.
,
т.к.
 .
.
2)
![]()
 - тоже первообразная для
- тоже первообразная для
![]() ,
т.к.
,
т.к.
![]() .
.
Таким образом, первообразная определяется не однозначно.
Теорема:
Если функция
является первообразной для
,
то функция
![]() ,
где
,
где
![]() – постоянная, также является первообразной
для
.
– постоянная, также является первообразной
для
.
Обратно:
Если
- первообразная для
,
то любая другая первообразная для
имеет вид
![]()
Доказательство:
1)
Пусть
первообразная для
,
это значит
![]() .
Требуется доказать, что
– первообразная. Продифференцируем
функцию.
.
Требуется доказать, что
– первообразная. Продифференцируем
функцию. .
Это означает, что
- тоже первообразная для
.
.
Это означает, что
- тоже первообразная для
.
2)
Пусть
- первообразная для
и
![]() - другая первообразная для
.
По определению первообразной это
означает, что:
- другая первообразная для
.
По определению первообразной это
означает, что:
 ,
но тогда эти функции могут отличаться
лишь на
,
но тогда эти функции могут отличаться
лишь на
![]() ,
т.е.
,
т.е.
![]() .
Теорема доказана.
.
Теорема доказана.
1.2. Понятие неопределенного интеграла и его свойства
Определение:
Неопределенным
интегралом функции
называется совокупность всех ее
первообразных, т.е.
.
Обозначается
 .
.
Процесс отыскания первообразной функции называется интегрированием данной функции.
Примеры:
1. ;
2.
;
2. ;
3.
;
3. .
.
Свойства неопределенного интеграла
Производная, от неопределенного интеграла, равна подынтегральной функции:
 .
.Дифференциал от неопределенного интеграла равен подынтегральному выражению
 .
.Интеграл от дифференциала какой-либо функции равен этой функции плюс постоянная:
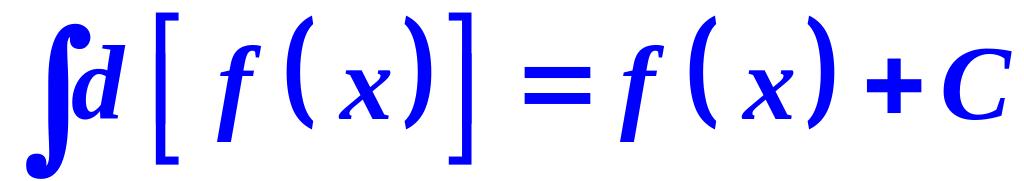 .
.
Пример.
1) ;
2)
;
2)
 .
.
Определение: Функция, неопределенный интеграл которой существует, называется интегрируемой.
Теорема: (достаточное условие существования неопределенного интеграла). Если функция непрерывна в промежутке х, то она интегрируема в этом промежутке.
1.3. Правила и формулы интегрирования Правила:
Множитель можно выносить за знак интеграла
 .
.Интеграл от алгебраической суммы функций равен сумме интегралов этих функций
 .
.Если интегрируется по t, то и первообразная записывается по t
 .
. .
.
Доказательство.

Случаи: ;
;
 .
.
Примеры:
1.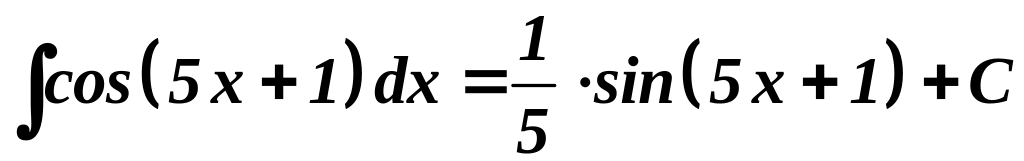 ;
2.
;
2. ;
;
3. .
.
Таблица интегралов
№/п |
Формула |
№/п |
Формула |
1 |
|
11 |
|
2 |
|
12 |
|
3 |
|
13 |
|
4 |
|
14 |
|
5 |
|
15 |
|
6 |
|
16 |
|
7 |
|
17 |
|
8 |
|
18 |
|
9 |
|
19 |
|
10 |
|
20 |
|
21 |
|
||
22 |
|
||
Таблица дифференциалов
№/п |
Формула |
№/п |
Формула |
1 |
|
12 |
|
2 |
|
13 |
|
3 |
|
14 |
|
4 |
|
15 |
|
5 |
|
16 |
|
6 |
|
17 |
|
7 |
|
18 |
|
8 |
|
19 |
|
9 |
|
20 |
|
10 |
|
21 |
|
11 |
|
22 |
|
Примеры.
Вычислить:
1) ;
2)
;
2)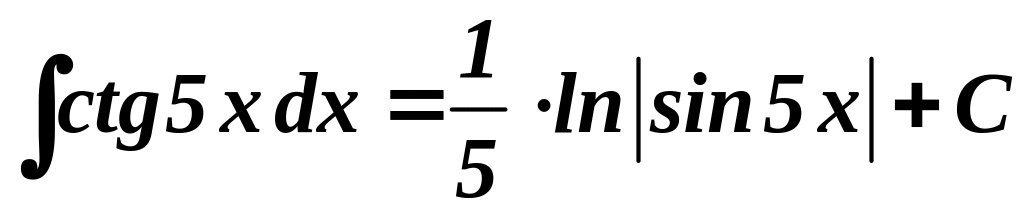 ;
;
3) ;
4)
;
4) ;
;
5) ;
;
6) .
.
2. Замена переменной в неопределенном интеграле
Пусть
требуется найти интеграл,
 и мы не можем воспользоваться формулами
непосредственно. Делаем замену
и мы не можем воспользоваться формулами
непосредственно. Делаем замену![]() ,
где
,
где
![]() -
непрерывна, дифференцируема, тогда:
-
непрерывна, дифференцируема, тогда:
 .
.
Алгоритм интегрирования методом замены переменной.
1. Определяют, к какому табличному интегралу приводится данный интеграл (предварительно преобразовав подынтегральное выражение, если нужно).
2. Определяют, какую часть подынтегральной функции заменить новой переменной, и записывают эту замену.
3. Находят дифференциалы обеих частей записи и выражают дифференциал старой переменной (или выражение, содержащее этот дифференциал) через дифференциал новой переменной.
4. Производят замену под интегралом.
5. Находят полученный интеграл.
6. В результате производят обратную замену, т.е. переходят к старой переменной. Результат полезно проверить дифференцированием.
Примеры:
1)

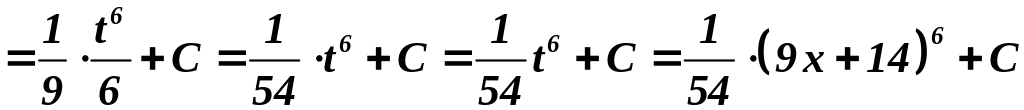 .
.
2)
3)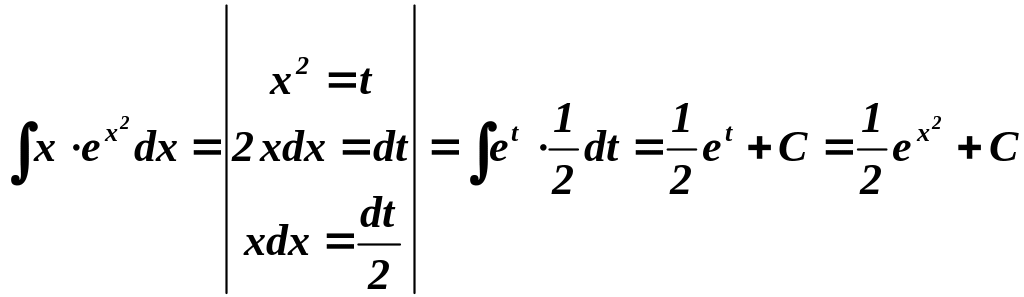 .
.