1 Тема

Понятие множества

Множеством называется совокупность некоторых элементов, объединенных каким-либо общим признаком. Элементами множества могут быть числа, фигуры, предметы, понятия и т.п.

Символика задания множеств, способы задания.

М ножество можно обозначить овалом, внутри которого точками изображены его элементы- называется диаграмма Эйлера- Венна

О сновные операции над множествами, их свойства

Общее определение функции м связанные с ним понятия

Функция — математическое понятие, отражающее связь между элементами множеств. Можно сказать, что функция это «закон», по которому каждому элементу одного множества (называемому областью определения x) ставится в соответствие некоторый элемент другого множества (называемого областью значений y) .

Теоретико-множественное определение

В теоретической математике функцию f удобно определить как бинарное отношение (то есть множество упорядоченных пар ), которое удовлетворяет следующему условию: для любого^[3] существует единственный элемент такой, что .

Это и позволяет говорить о том, что элементу сопоставлен один и только один элемент такой, что .

Таким образом, функция — это упорядоченная тройка (или кортеж) объектов (f,X,Y), где

• множество X называется о́бластью определе́ния;

• множество Y называется о́бластью значе́ний;

• множество упорядоченных пар 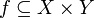или, что то же самое, график функции.

Если задана функция f, которая определена на множестве X и принимает значения в множестве Y, значит, функция f отображает множество X в Y

2 Тема

Вещественные числа и векторное пространство.

Вещественные числа и числовая прямая

Вещественные числа- это действительные. Коротко говоря, это числа которые могут быть обозначены на числовой прямой, но у которых не обязательно будет конечная или периодическая дробная часть( она может быть бесконечной- например √2).

Числовая (координатная) ось – прямая, на которой выбрана начальная точка (начало) О, выделено положительное направление, которое обозначается стрелочкой (противоположное направление считается отрицательным) и единица масштаба или масштабный отрезок ОА. С помощью точек числовой оси изображаются действительные числа. Точке О соответствует нуль, точке А -1, и т.д. (Рис.1.)

Рис.1.

Интервалы могут быть:

1.      открытый интервал (а,b) – совокупность всех точек числовой оси, лежащих строго между точками а и b;

2.      замкнутый интервал [a,b] – совокупность точек числовой оси, расположенных между а и b, включая сами точки а и b;

3.      полуоткрытые интервалы – интервалы вида [а,b) или (a,b];

4.      бесконечные интервалы (а, ∞) или (-∞,b) – множество точек которые находятся справа от числа а (больше числа а) или слева от числа b (меньше числа b). Вся числовая ось может рассматриваться как бесконечный интервал (-∞,∞).

Окрестность точки. 1. На числовой оси окрестность точки – любой интервал (открытый промежуток), содержащий данную точку. В частности открытый (не содержащий границ) промежуток (а – δ; а + δ) с центром в точке а называется δ-окрестностью точки а (положительное число δ – радиус δ-окрестности).   

Расширенное множество вещественных чисел

Мнимые числа[2]), — расширение множества вещественных чисел, обычно обозначается . Любое комплексное число может быть представлено как формальная сумма x + iy, где x и y — вещественные числа, i — мнимая единица[3].

Функция многих переменных

Функция двух переменных. Переменная (с областью изменения  ) называется функцией независимых переменных  в множестве  , если каждой паре их значений из  по некоторому правилу или закону ставится в соответствие одно определенное значение  из множества . Множество v область определения функции, множество  v область ее значений. Функциональная зависимость   от обозначается так:  и т.п. Выберем в пространстве систему координат  , изобразим на плоскости  множество  ; в каждой точке этого множества восстановим перпендикуляр к плоскости и отложим на нем значение . Геометрическое место полученных таким образом точек и является пространственным графиком функции двух переменных.

Аналогчно и с большим числом аргументов- каждой упорядоченной тройке, четверке, пятерке и.т.д аргументов, соответствует единственное значение из некоторого меножества.

Числовые последовательности

Последовательностью называется множество чисел, перенумерованных с помощью натуральных чисел и расставленных в порядке возрастания их номеров x₁,x₂,...x_n Числа x₁,x₂,...,x_n — называются элементами последовательности, символ x_n — общим элементом, а число n — его номером. Сокращенно последовательность обозначается символом {x_n}.

Способ задания функции

1 Функцию можно задать непосредственно как множество упорядоченных пар, например:

2 Если ввести переменную x, пробегающую множество и переменную y, пробегающую множество , указанную функцию можно задать аналитически, как: .

Аналогично можно задавать числовые функции. Например: где х пробегает множество вещественных чисел задает некоторую функцию f. Важно понимать, что само выражение не является функцией. Функция как объект представляет собой множество (упорядоченных пар). А данное выражение как объект есть равенство двух переменных. Оно задает функцию, но не является ею.

Однако, во многих разделах математики, можно обозначать через f(x) как саму функцию, так и аналитическое выражение, ее задающее. Это синтаксическое соглашение является крайне удобным и оправданным.

3 Графический :

Если в качестве линейного пространства взять евклидово пространство свободных геометрических векторов (направленных отрезков), а число аргументов функции f не превосходит 2, указанное множество точек можно изобразить наглядно в виде чертежа (графика). Если сверх того исходный базис взять ортонормированным, получим "школьное" определение графика функции. Каждой упорядоченной паре(тройке) точек , находящихся на осях координат соответствует точка на плоскости ( в пространстве) построенная отложением отрезков на этих осях. И множество этих точек образуют линию или плоскость, называемую графиком.

Для функций 3 аргументов и более такое представление не применимо ввиду отсутствия у человека геометрической интуиции многомерных пространств.

4 табличный

Системы координат

Прямоугольными декартовыми координатами называют две взаимно перпендикулярные числовые оси ОХ и ОУ, имеющие одинаковые или различные масштабные единицы. Точка О – начало координат, прямые ОХ и ОУ называют осями координат, ось ОХ называют осью абсцисс, ось ОУ – осью ординат. Плоскость, на которой задана система координат, называют координатной плоскостью. (Рис.3.)

                                             

                                Рис.3.

Каждой точке координатной плоскости соответствует пара чисел. Например, точке А соответствует пара чисел (2,1). Говорят, что точка А имеет координаты 2 и 1. Первое число всегда откладывают на оси ОХ (абсцисс), второе – на оси ОУ (ординат). Точка О имеет координаты (0,0).

Рис. 4: Полярные системы координат

Полярными координатами точки P называются радиус-вектор ρ - расстояние от точки P до заданной точки O (полюса) и полярный угол φ - угол между прямой OP и заданной прямой, проходящей через полюс (полярной осью). Полярный угол считается положительным при отсчете от полярной оси против часовой стрелки и отрицательным при отсчете в обратную сторону.

Формулы для перехода от полярных координат к декартовым

x=ρ*cos(φ), y=ρ*sin(φ)

Параметрическое представление функции

Предположим, что функциональная зависимость y от x не задана непосредственно y = f(x), а через промежуточную величину — t. Тогда формулы

  

задают параметрическое представление функции одной переменной.

Графиком функции называется множество точек плоскости, абсциссами которых служат значение аргумента х, а ординатами – соответствующие им значения функции у.

Неявная функция

Рассмотрим функцию

Мы видим, что слева у нас одинокий «игрек» (функция), а справа – только «иксы». То есть, функция  в явном виде выражена через независимую переменную .

Рассмотрим другую функцию:  

Здесь переменные  и  расположены «вперемешку». Причем никакими способами невозможно выразить «игрек» только через «икс».

Это и есть неявная функция.

Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательное, либо всегда неположительное. Если в дополнение приращение не равно нулю, то функция называется стро́го моното́нной. Монотонная функция — это функция, меняющаяся в одном и том же направлении.

Обратная функция и ее график

Если в заданной явно функции , где у выражен через х – «оголить » х, т.е выразить его через у – получится обратная функция.

Графики взаимно обратных функция симметричны относительно прямой y=x

Суперпозиция функция

 Пусть имеются две функции: z = h(y) и y = g(x), причем область значений функции g принадлежит области определения функции h. Тогда функция z = h(g(x)) называется композицией функций h и g, или сложной функцией, или суперпозицией функций. Аналогично можно рассматривать композицию любого конечного числа функций.

Те тоже самое что и сложная функция.

Арифметические операции над функциями

Теорема. Если две функции и определены в одном и том же промежутке и обе непрерывны в точке то в той же точке будут непрерывны и функции

(последняя — при условии, что

Четные, нечетные, периодические функции

Четные: это когда функция от а равна функции от –а. График симметричен относительно оси у.

Нечетные : функция от -а равна : –функции от а График симметричен относительно начала координат.

Периодическая: когда функция от а равна функции от (а+ период). График повторяется через определенный период.

Ограниченность функции.

Функция f(x) называется ограниченной на данном промежутке (a,b), если существуют некоторые числа m и M такие, что

m ≤ f(x) ≤ M

при хє(a,b).

Число m_o= inf {f(x)} [x є (a,b)] = min m называется нижней гранью функции ,

а число M_o= sup {f(x)} [x є (a,b)]= max M называется верхней гранью функции на данном промежутке (a,b).

Разность M_o- m_o называется колебанием функции на промежутке (a,b).

Тема 3 Пределы функций и последовательностей.

Число b,

к которому стремится функция при стремлении x к числу _, называется пределом функции. Вот так

это все записывается:

limf(x) =b при x→a(пишется под lim)

Определение предела функции в точке.

Пределом функции в точке а( лежит на х) называется такое число А( лежит на у) если для любого ε (эпсилон- окрестность точки А ) найдется такая δ(дельта- окрестность точки а) что если модуль разности х и а меньше дельты, то модуль разности f(x) и А меньше эпсилона.

Теорема о единственности предела

 Если функция имеет предел в точке а, то этот предел единственный для этой точки.

Ограниченность функции имеющей предел

Теорема об ограниченности функции

Если функция в некоторой окрестности имеет предел, то она в этой окрестности ограничена.

Предел функции на бесконечности

Определение предела функции в бесконечности.

Пределом функции в бесконечности называется число А (лежит на у) если для любого эпсилона найдется такое число М что если х меньше М то модуль разности f(x) и А меньше эпсилона.

Предел последовательности

Число а называется пределом последовательности если

что для любого существует такой номер , что все c номерами расположены между и .

Последовательность, предел которой - конечное число , называется сходящейся, и ее предел обозначают

Бесконечно большие величины и бесконечный предел

Если переменная x стремиться к бесконечности, то ее называют бесконечно большой переменной величиной и пишут

x→∞.

по мере стремления к значения неограниченно возрастают (убывают) и могут по модулю превзойти любое положительное число N, как бы велико оно ни было. Говорят, что бесконечно большая переменная имеет бесконечный предел.

О п р е д е л е н и е 5. Функция y = f (x)  называется бесконечно большой величиной при , если для каждого положительного сколь угодно большого числа N найдется соответствующее сколь угодно большое число K(N) такое, что для всех х, удовлетворяющих неравенству , будет выполняться неравенство :

Бесконечно малые величины и их свойства

О п р е д е л е н и е 1. Функция y = f (x) называется бесконечно малой величиной (Б.М.В.) при , если ее предел равен нулю

1. Сумма (разность) бесконечно малых величин есть величина бесконечно малая:

2. Произведение бесконечно малых величин есть величина бесконечно малая:

3. Произведение бесконечно малой величины на константу С или на функцию, имеющую конечный предел , есть величина бесконечно малая:

Взаимные свойства бесконечно малых и бесконечно больших величин

1. Сумма бесконечно больших величин есть величина бесконечно большая:

2. Произведение бесконечно больших величин есть величина бесконечно большая:

3. Произведение бесконечно большой величины на константу С, или на функцию, имеющую конечный предел , есть величина бесконечно большая:

4. Величина, обратная бесконечно малой величине, есть величина бесконечно большая, и наоборот, величина, обратная бесконечно большой величине, есть величина бесконечно малая.

Теоремы о пределах функций

Теорема 1. (о единственности предела функции). Функция не может иметь более одного предела.

Теорема 2. Если функции f(x) и  g(x) имеют пределы в точке , то:

1) предел алгебраической суммы функций равен алгебраической сумме пределов слагаемых, т.е.

2) предел произведения функций равен произведению пределов сомножителей,

предел частного двух функций равен частному от деления предела делимого на предел делителя, если предел делителя не равен нулю,

Теорема 3 (о пределе сложной функции). Если существует конечный предел

а функция f(u) непрерывна в точке , то

Другими словами, для непрерывных функций символы предела и функции можно поменять местами.

Представление функции имеющей предел

Для того чтобы функция  имела при  конечный предел , необходимо и достаточно, чтобы функция   была бесконечно малой при .

Предельный переход в неравенствах

Если две функции удовлетворяют неравенству, и все значения одной функции в окрестности точки а больше значений другой функции, и обе имеют предел в точке а то пределы этих функции тоже удовлетворяют этому неравенству.

Если есть три функции удовлетворяющие неравенству g(x)<=f(x)<=w(x) И пределы g(x) и w(x) в точка а =А, и f(x) тоже имеет предел в этой точке то он тоже = А.

Монотонные последовательности

числовая последовательность  a₁, a₂, a₃, ...  называется монотонно возрастающей, если для любого п

a_n+1 > a_n

Критерий сходимости Коши

Пусть задана числовая последовательность {x_n}. Эта последовательность сходится тогда и только тогда, когда для любого числа ε > 0 существует номер N такой, что при всех n > N  и любых натуральных m выполняется неравенство (т.е. расстояние между членами последовательности с номерами n  и n+m меньше ε) – критерий Коши сходимости последовательности.

Неопределенные выражения

П ри вычислении пределов возможны следующие комбинации бесконечно малых и бесконечно больших величин, которые называются неопределенностями:

Предел рациональной дроби

Если нужно найти предел от дроби в которой числитель и знаменатель представляют собой некоторые многочлены ( рациональная дробь), рекомендуется сократить эту дробь один или несколько раз на бином (х-а).

Первый и второй замечательные пределы 

Теорема 2.14   Первый замечательный предел равен

Вторым замечательным пределом называется предел

Сравнение бесконечно малых величин и их эквивалентность

Определение 4.1. Функции и называются бесконечно малыми величинами одного порядка малости, если .

Определение 4.4. Функция называется бесконечно малой величиной более высокого порядка малости, чем , если .

Определение 4.3. Функция называется бесконечно малой величиной более низкого порядка малости, чем , если .

Односторонние пределы

Функция может иметь разный предел при стремлении аргумента к числу х с разных сторон.

Справа х+0 и слева х-0

Существует два принципиально разных случая когда разница между этими пределами конечная – разрыв первого рода и

Разница между пределами – бесконечная- разрыв второго рода.

Тема 4

Непрерывность функции

1.Функция называется непрерывной в точке а если она определена в этой точке, и имеет предел в этой точке равный f(a).

2. Если при стремлении приращения аргумента к нулю, функция стремится приращение функции стремится к нулю- то в этой точке функция непрерывна.

3 Если односторонние пределы и предел функции в точке а равны, то функция в этой точке непрерывна.

Равномерная непрерывность

Если на интервале (а b) взяты точки х’ и x” и для любого эпсилон найдется такая дельта, что расстояние между иксами будет меньше дельты, и при этом расстояние между значениями функции от этих иксов будет меньше эпсилона, то такая функция будет равномерно непрерывной.

Классификация точек разрыва

Если предел функции в точке а равен А, а значение функции в этой точке равен В то в этой точке функция претерпевает разрыв.

Если расстояние между односторонними пределами в точке а конечное число, это это точка разрыва первого рода, а если бесконечность ( т.е. если хотя бы с одной стороны функция в этой точке уходит в бесконечность) то это точка разрыва второго рода..

Есть еще устранимая точка разрыва, когда предел функции в точке не равен значению функции в точке. В этом случае функцию можно доопределить и присвоить функции в этой точке значение равное пределу, и таким образом устранить разрыв.

Свойства непрерывных функций

Если значение функции в некоторой точке а больше ( или меньше) А то можно найти эпсилон- окрестность ( окрестность с радиусом эпсилон) точки а, что значения функции для точек из этой окрестности тоже будут больше ( меньше )А.

Если значение функции в некоторой точке а больше нуля ( или меньше нуля), то существует такая эпсилон окрестность в которой все точки, ей принадлежащие будут давать значение функции тоже больше нуля ( или меньше).

Сумма , разность произведение, частное и сложная функция в точке а будут непрерывны, если все функции- участники этих действий непрерывны в этой точке.

Если функция непрерывна на отрезке, то она непрерывна на любом интервале, входящем в этот отрезок и на любой точе принадлежащей этому отрезку.

Теорема Вейерштрасса

Если функция непрерывна на отрезке [а b] то она на нем ограничена,т. Е. имеет верхний и нижний предел.