Остаточный член формулы Тейлора в форме Лагранжа

Остаточный член в форме   дает лишь качественную оценку  . Хотелось бы иметь более точную количественную оценку. Такую оценку часто позволяет получить остаточный член в форме Лагранжа.

Рассмотрим еще раз выражение для 

Рассмотрим функцию

Обратите внимание, как строиться выражение для функции  : в выражение для  вместо   ставиться аргумент z.

Очевидно, что

, 

Далее вычислим 

.

Рассмотри еще функцию  . Для нее

;  ;  .

А теперь воспользуемся формулой Коши

,  .

Подставляя сюда соответствующие члены, получим

Отсюда получается выражение для остаточного члена  :

,  .

Эта форма остаточного члена и называется остаточным членом в форме Лагранжа. Ее дальнейшее использование заключается в том, что пытаются оценить сверху  , т.е. ищут такое  , что  .

Тогда

что и позволяет оценивать погрешность от использования формулы Тейлора для вычисления  . Сама формула Тейлора с остаточным членом в форме Лагранжа имеет вид

,

где  . В частном случае 

Эта формула носит название ряда Маклорена с остаточным членом в форме Лагранжа.

20. Применение формул Тейлора и Маклорена для приближенных вычислений и вычисления пределов.

Применение формулы Тейлора для нахождения пределов и приближённых вычислений.

 7.9.1. Нахождение пределов с помощью формулы Тейлора. Рассмотрим примеры:

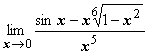. Так как в знаменателе стоит х5, то при представлении функций, стоящих в числителе, по формуле Маклорена, мы должны брать многочлены не ниже пятой степени:  ;   (следующий член разложения имеет шестую степень)  ,

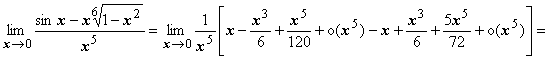
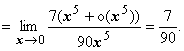
2.  . Здесь мы в выкладках обязаны удерживать члены до четвёртой степени: 

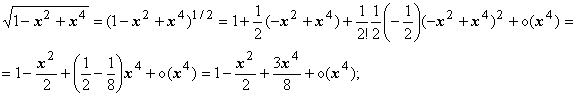
поэтому  .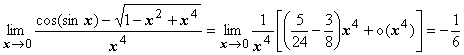

 7.9.2. Приближённые вычисления с помощью формулы Тейлора. В разделе 6.8.4 Применение дифференциала в приближённых вычислениях мы пользовались выражением у(x+х) у(x)+ у'(x) х, которое, как теперь очевидно, содержит два первых члена формулы Тейлора. Формула Тейлора обобщает это выражение; она позволяет проводить более точные вычисления и оценивать точность этих вычислений. Рассмотрим следующий пример: требуется вычислить sin1 с погрешностью, не превышающей 0,00001. Остаточный член в форме Лагранжа для функции   имеет вид , следовательно  . Подбором находим, что  , следовательно, мы должны взять степени х вплоть до седьмой:

21. Определение, геометрический и механический смысл производной функции.

22. Производная сложной, обратной функции и функции, заданной параметрически.\

Производная сложной функции ~ Производная обратной функции

Производная сложной функции.Пусть     - функция, дифференцируемая в точке   ,    - функция, дифференцируемая в точке    , причем   . Тогда    - сложная функция независимого переменного  , дифференцируема в точке     и ее производная в этой точке вычисляется по формуле    .

Обычно     называют внешней функцией, а  - внутренней. При вычислении производной сложной функции сначала дифференцируют внешнюю функцию, не обращая внимания на внутреннюю (ведь она может быть любой), затем умножают на производную конкретной внутренней функции.

ПРИМЕР 1.  Вычисление производных сложных функций

Производная обратной функции.

Пусть функция  дифференцируема и строго монотонна на  . Пусть также в точке  производная  . Тогда в точке    определена дифференцируемая функция  , которую называют обратной к   , а ее производная вычисляется по формуле  .