18. Связь между аналитическими и гармоническими функциями.

19. Интеграл от функции комплексного переменного, его свойства и вычисление. Вычисление интеграла от функции f(z) комплексного переменного z сводится к вычислению обычных криволинейных интегралов, а именно: где С кусочно-глаткая замкнутая или незамкнутая ориентированная  кривая, лежащая в D. Если f(z) аналитическая функция в односвязной области D, то интеграл не зависит от пути интегрирования. В этом случае Если кривая С задана параметрическими уравнениями x=x(t), y=y(t) и начальные и конечные точки дуги С соответствуют значения параметра t₀ и t₁, то где z(t)=x(t)+iy(t). Все свойства интегралов сохраняются для(такие как умножение на const…). Если функция f(z) аналитична в односвязной D, содержащей точки z₀ и z₁, то имеет место формула Ньютона-Лейбница. где F(z)-какая-либо первообразная для функция f(z), т.ч. в области D F ^/(z)= f(z)

20. Интеграл от аналитической функции. Основная теорема Коши для односвязных и многосвязных областей  где n – целое, С- замкнуты контур. 1)n<0 2)n³0: Если точка а внутри С то интеграл не равен 0. Теорема Коши не зависит от пути интегрирования при  Теорема Коши: Если функция f(z) – аналитична в односвязной области G, ограниченная замкнутая контуром С, а также и на контуре С, то: Доказательство: Пусть f(z) непрерывна. Эти два интеграла тоже, что и криволинейный интеграл 2-го рода. Так как f(z) аналитична выполняется условие Коши-Римана. После подстановки условий К-Р можно сделать вывод, что (Теорема верна без предположения, что f(z) непрерывна) . Пункт 2. Пусть область G  многосвязная. Рассмотрим многосвязную область G, ограниченную внешним контуром С₀ ивнутренними контурами С₁,С₂,…,С_n.  Пусть f(z)- аналитичная в области G  и на контурах С₁,С₂,…,С_n. (С=С₀ÈС₁È…È С_n). Пусть   По замкнутому контуру С_k , обходится против часовой стрелки. Соединим контура между собой дугами  Область G разобьется на две односвязные области Г^/  и Г^// которые ограничиваю две односвязные области. Функция f(z) аналитична на контурах Г^/  и Г^// и в односвязных облостях которые они ограничивают. Из теоремы коши будем иметь: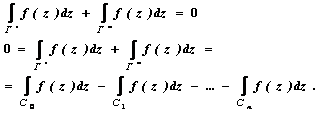  При сложении интегралов в левой части интегралы сократятся в силу того, что при обходе по первому контуру мы берем их со знаком плюс при обходе по второму контуры берем со знаком минус.

Пункт 3. Если интеграл f(z) по любому замкнутому контуру расположенному внутри области G равен 0 то интеграл по любой дуге принадлежащей G зависит только от начальной и конечной точек этой дуги и не зависит от пути интегрирования. Т.е. одинаков для всех дуг, имеющих общую начальную и конечную точки.

21. Интегральная формула Коши для аналитической функции и ее производных. Пусть f(z)- аналитичная в односвязной области G и на контуре Г, ограничивающую эту область G и пусть точка Z любая точка внутри контура, тогда имеет место интегральная формула Коши: Доказательство: g - окружность с центром в точке z и радиусом r причем gÎG. По теореме Коши для составного контура будем иметь. Доказав (**). Подставим в (***).

22. Степенные ряды комплексного переменного и их свойства. Пусть переменная а принимает последовательно значения а₁,а₂,а₃,…,а_n. Такое перенумерованное множество чисел называется последовательностью. Она бесконечна. Числовым рядом называется выражение а₁+а₂+а₃+…+а_n+…=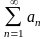 . Числа а₁,а₂,а₃,…,а_n – члены ряда. Например. а₁ – первый член ряда. а_n – n-ый или общий член ряда. Ряд считается заданным, если известен n-ый (общий член ряда).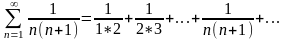 Числовой ряд имеет бесконечное число членов.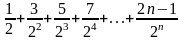 Числители – арифметическая прогрессия (1,3,5,7…). n-ый член находится по формуле а_n=а₁+d(n-1); d=а_n-а_n-1. Знаменатель – геометрическая прогрессия. b_n=b₁q^n-1; 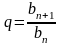. Рассмотрим сумму первых n членов ряда и обозначим ее Sn. Sn=а1+а2+…+а_n. Sn – n-ая частичная сумма ряда. Рассмотрим предел: S - сумма ряда. Ряда сходящийся, если этот предел конечен (конечный предел S существует). Ряд расходящийся, если этот предел бесконечен. В дальнейшем наша задача заключается в следующем: установить какой ряд. Одним из простейших, но часто встречающихся рядов является геометрическая прогрессия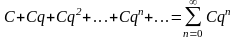 , C=const. Геометрическая прогрессия является сходящимся рядом, если 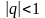, и расходящимся, если 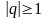. Также встречается гармонический ряд (ряд ). Этот ряд расходящийся. Свойства числовых рядов.

1. Если сходится а₁+а₂+а₃+…+а_n+…= , то сходится и ряд а_m+1+а_m+2+а_m+3+…, полученный из данного ряда отбрасыванием первых m членов. Этот полученный ряд называется m-ым остатком ряда. И, наоборот: из сходимости m-го остатка ряда вытекает сходимость данного ряда. Т.е. сходимость и расходимость ряда не нарушается, если прибавить или отбросить конечное число его членов.

2. Если ряд а₁+а₂+а₃+… сходится и его сумма равна S, то ряд Са₁+Са₂+…, где С= так же сходится и его сумма равна СS.

3. Если ряды а₁+а₂+… и b₁+b₂+… сходятся и их суммы равны соответственно S1 и S2, то ряды (а₁+b₁)+(а₂+b₂)+(а₃+b₃)+… и (а₁-b₁)+(а₂-b₂)+(а₃-b₃)+… также сходятся. Их суммы соответственно равны S1+S2 и S1-S2.

4. а). Если ряд сходится, то его n-ый член стремится к 0 при неограниченном возрастании n (обратное утверждение неверно).

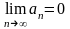- необходимый признак (условие) сходимости ряда.

б). Если 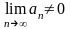то ряд расходящийся – достаточное условие расходимости ряда.

-ряды такого вида исследуются только по 4 свойству. Это расходящиеся ряды.

23. Ряды Тейлора. Разложение основных элементарных ФКП в ряды Маклорена. Если функция f (x) имеет непрерывные производные вплоть до (n+1)-го порядка, то ее можно разложить в степенной ряд по формуле Тейлора: где R_n − остаточный член в форме Лагранжа определяется выражением Если приведенное разложение сходится в некотором интервале x, т.е. , то оно называется рядом Тейлора, представляющим разложение функции f (x) в точке a. Если a = 0, то такое разложение называется рядом Маклорена: Разложение некоторых функций в ряд Маклорена











24. Ряд Лорана, его кольцо сходимости. Разложение функции в ряд Лорана.  Как уже отмечалось, аналитической функции f(z) всегда можно сопоставить степенной ряд , который сходится к функции f(z) окрестности точки z₀ или в круге . Точка z₀ такого типа называется правильной точкой функции f(z). Например, все точки будут правильными для функции , как это следует из свойств ряда. Таким образом, с помощью степенных рядов можно исследовать поведение функции f(z ) в окрестности ее правильных точек. Наоборот, точки, которые не являются правильными для функции f(z), называются ее особыми точками. Так, для z = 1ряд не будет сходиться, а для функции эта точка будет особой. Поведение функции f(z ) в окрестности ее особой точки можно исследовать с помощью ряда Лорана, который определяется как степенной ряд следующего вида:

при этом называют    - главной;    - правильной частью ряда.

25. Изолированные особые точки аналитической функции, их классификация. Точка а С_z называется изолированной особой точкой однозначного характера функции f (z), если f (z) аналитическая и однозначная (регулярная) в кольце {z:0<|z–a|< }, а в самой точке а не определена. Бесконечно удаленная точка называется изолированной особой точкой однозначного характера функции f (z), если f (z) регулярна в некоторой окрестности {R<|z|<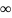 } точки z= и функция имеет в точке  =0 изолированную особую точку однозначного характера. В зависимости от поведения функции f (z) вблизи точки а различают следующие три типа особых точек. Изолированная особая точка а функции f (z) называется а) устранимой особой точкой, если существует конечный предел б) полюсом, если в) существенно особой точкой, если не существует. Заметим, что типы особых точек z= функции f (z) и =0 функции совпадают, ибо Порядком (или кратностью) полюса функции g(z) в точке а называется кратность нуля в точке а регулярной функции Если а – простой нуль f (z), то точка а называется простым полюсом функции g(z).

26. Вычеты. Вычисление вычетов. Теорема о вычетах. Пусть f(z) — комплекснозначная функция в области , голоморфная в некоторой проколотой окрестности точки , f(z) в a называется число . Согласно определению вычет может быть вычислен как контурный интеграл, однако в общем случае это довольно трудоёмко. Поэтому на практике пользуются, в основном, следствиями из определения: В устранимой особой точке , так же как и в точке регулярности, вычет функции f(z) равен нулю. В то же время для бесконечно удалённой точки это утверждение не верно. Например, функция имеет в бесконечности нуль первого порядка, однако, . Причина этого в том, что форма имеет особенность как в нуле, так и в бесконечности. В полюсе a кратности n вычет может быть вычислен по формуле: , частный случай n = 1 .Если функция имеет простой полюс в точке a, где g(z) и h(z) голоморфные в окрестности a функции, h(a) = 0, , то можно использовать более простую формулу: . Очень часто, особенно в случае существенно особых точек, удобно вычислять вычет пользуясь разложением функции в ряд Лорана. Например, , так как коэффициент при z ^{− 1} равен 1. Теорема Если f аналитична в некоторой замкнутой односвязной области , за вычетом конечного числа особых точек , из которых ни одна не принадлежит граничному контуру , то справедлива следующая формула: , где  — вычет f в точке a_k. Для использования теоремы в вычислении вещественных интегралов нужно продолжить интегрируемую функцию на комплексную плоскость и найти ее вычеты, что обычно довольно просто сделать. После этого нужно замкнуть контур интегрирования, добавив к вещественному отрезку полуокружность, лежащую в верхней или нижней комплексной полуплоскости. После этого интеграл по этому контуру можно вычислить, использую основную теорему о вычетах. Зачастую интеграл по полуокружности можно устремить к 0, выбрав ее правильным образом, после чего контурный и нтеграл станет равен вещественному.

27. Случайные события и операции над ними. Несовместимые события. Полная группа событий. Опыт со случайным исходом – это комплекс условий, в которых происходит то или иное явление. Результат опыта – случайное событие. Заранее оговорено, что представляют собой возможные исходы опыта. Случайные события разделяют на элементарные (неразложимые) и составные (разложимые). Достоверное событие заведомо произойдет в результате данного опыта. Невозможное событие заведомо не произойдет в результате данного опыта. События называют несовместными, если появление одного из них исключает появление других событий в одном и том же опыте. События nAAA,...,,21 образуют полную группу событий, если в результате опыта появится хотя бы одно из них. В частности, если события, образующие полную группу, попарно несовместны, то в результате испытания появится одно и только одно из них. События A и B называются равносильными (равными), если в результате опыта они одновременно происходят или не происходят. Событие A влечет событие B ( BA ), если из того, что наступает событие A следует наступление события B , т.е. A является частным случаем B . Разностью событий A и B называется событие A \ B , которое происходит тогда и только тогда, когда наступает событие A, но наступает событие B .Противоположным событию A называется событие A, которое происходит тогда и только тогда, когда не наступает событие A. Суммой (объединением) событий A и B называется событие BA или BA, которое происходит тогда и только тогда, когда наступает хотя бы одно из событий A или B , т.е. когда наступает событие A или событие B , или оба события A и B .Произведением (пересечением) событий A и B называется событие AB или BA, которое происходит тогда и только тогда, когда происходят оба события A и . Замечание. Понятие суммы и произведения событий обобщаются на любое конечное число событий. По́лной гру́ппой собы́тий в теории вероятностей называется система случайных событий такая, что в результате произведенного случайного эксперимента непременно произойдет одно из них. Сумма вероятностей всех событий в группе всегда равна 1.

28. Равновозможные события. Классическое определение вероятностей. События А и В называют равновозможными, если не существует никаких объективных причин, вследствии которых при многократном повторении опыта одно из них наступает чаще, чем другое. Классическое определение вероятности. Как было сказано выше, при большом числе n испытаний частота P*(A)=m/n появления события A обладает устойчивостью и дает приближенное значение вероятности события A, т.е. . Это обстоятельство позволяет находить приближенно вероятность события опытным путем.   Два события называются равновероятными (или равновозможными), если нет никаких объективных причин считать, что одно из них может наступить чаще, чем другое. Так, например, появления герба или надписи при бросании монеты представляют собой равновероятные события. Рассмотрим другой пример. Пусть бросают игральную кость. В силу симметрии кубика можно считать, что появление любой из цифр 1, 2, 3, 4, 5 или 6 одинаково возможно (равновероятно). События E1,E2, ..., EN в данном опыте образуют полную группу, если в результате опыта должно произойти хотя бы одно из них. Так, в последнем примере полная группа событий состоит из шести событий — появлений цифр 1, 2, 3, 4, 5 и 6.  Очевидно, любое событие A и противоположное ему событие образуют полную группу. Событие B называется благоприятствующим событию A, если наступление события B влечет за собой наступление события A.  Так, если A — появление четного числа очков при бросании игральной кости, то появление цифры 4 представляет собой событие, благоприятствующее событию A. Пусть события E1,E2, ..., EN в данном опыте образуют полную группу равновероятных и попарно несовместных событий. Будем называть их исходами испытания. Предположим, что событию A благоприятствуют M исходов испытания. Тогда вероятностью события A в данном опыте называют отношение M/N. Итак, мы приходим к следующему определению. Вероятностью P(A) события в данном опыте называется отношение числа M исходов опыта, благоприятствующих событию A, к общему числу N возможных исходов опыта, образующих полную группу равновероятных попарно несовместных событий:  

29. Геометрическое и статическое определение вероятностей. Иногда недостаток конечного числа возможных исходов испытания можно преодолеть, используя геометрическое определение вероятности. Рассмотрим некоторую замкнутую область G в пространстве Обозначим через ее меру. Если область – одномерная (отрезок), то мерой будет ее длина, если область двумерная (некоторая плоская фигура), то ее мера - площадь, если трехмерная (тело в пространстве), то – объем. Пусть область D полностью содержится в области G. Мера области D - . Рассмотрим следующий эксперимент: случайно из области G выбирается точка А. Необходимо определить вероятность попадания точки А в подобласть D. Роль элементарных событий в данном эксперименте играют точки области G. Все множество точек области G образует пространство элементарных событий. Все элементарные события – равновозможны, так как все точки области G равноправны в отношении попадания туда случайной точки A. Но число этих элементарных событий бесконечно. Поэтому в данном случае классическое определение вероятности не применимо. Согласно геометрическому определению, вероятность случайного события А равна отношению меры области, благоприятствующей появлению события А, к мере всей области, т.е. .Итак, статистическая вероятность случайного события А равна относительной частоте появления этого события в ряде испытаний, т.е. , где m – число испытаний, в которых появилось событие А; n – общее число испытаний. Это и есть статистическое определение вероятности.

30. Теорема о вероятности суммы событий. Рассмотрим теоремы, позволяющие вычислить вероятность появления события А или В в результате одного испытания, т.е. вероятность суммы этих событий А+В. Возможны два случая: события совместны и несовместны. Теорема1: Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий: Р(А+В)=Р(А)+Р(В). Доказательство: Число всех исходов N, число исходов благоприятствующих событию А- К, событию В- L. Так как А и В несовместны, то ни один из этих исходов не может благоприятствовать А и В одновременно, т.е. А и В взаимно исключающие, следовательно число благоприятствующих исходов для события А+В равно К+L. Тогда вероятность равна  Теорема2: Вероятность суммы двух совместных событий А и В равна сумме их вероятностей без вероятности их совместного появления, т.е. Р(А+В)=Р(А)+Р(В)-Р(АВ). Доказательство: Всего исходов N, благоприятствующих событию А- К, событию В- L, совместному появлению А и В- М. Следовательно, благоприятных исходов для события А+В : K+L-M. Откуда вероятность события А+В:

31. Условная вероятность. Независимость событий. Теорема о вероятности произведения событий. Условная вероятность — вероятность одного события при условии, что другое событие уже произошло. Определение . Условной вероятностью события А при условии, что произошло событие В, называется число Условная вероятность определена только в случае, когда Независимость событий. Без преувеличения можно сказать, что понятие независимости является одним из ключевых в теории вероятностей. Мы начинаем с обсуждения независимости двух событий. Определение 1.6   События А и В называются независимыми, если Замечание 1.1   Если А и В независимы и , то Аналогично, если А и В независимы (и ) Произведением событий A и B называют событие, состоящее в совместном появлении этих событий. Произведением нескольких событий A1,A2,...,Ak называют событие, состоящее в совместном появлении всех этих событий. p(A∖B)−  вероятность события A при условии, что B уже произошло.

32. Формула полной вероятности. Формула Байеса.  Пусть событие A может произойти только вместе с одним из попарно несовместных событий H1, H2, ..., Hn, образующих полную группу. Тогда, если произошло событие A, то это значит, что произошло одно из попарно несовместных событий H1A, H2A, ..., HnA. Следовательно,   Применяя аксиому сложения вероятностей, имеем   Но (i=1, 2, ..., n), поэтому  Эта формула называется формулой полной вероятности. События H1, H2, ..., Hn часто называют «гипотезами». Формула Байеса: , где P(A) — априорная вероятность гипотезы A (смысл такой терминологии см. ниже); P(A | B) — вероятность гипотезы A при наступлении события B (апостериорная вероятность); P(B | A) — вероятность наступления события B при истинности гипотезы A; P(B) — вероятность наступления события B.

33. Схема независимых испытаний Бернулли. Формула Бернулли.   Проводится серия из n независимых испытаний, каждое из которых заканчивается либо “успехом” либо “неуспехом”, в каждом испытании (опыте) вероятность успеха p, а вероятность неуспеха q=1-p. Вероятность того, что в серии будет реализовано ровно k “успехов” вычисляется по формуле , где 0<p<1, k=0, 1,., n, , . Теорема: Если Вероятность p наступления события Α в каждом испытании постоянна, то вероятность P_k,n того, что событие A наступит k раз в n независимых испытаниях, равна: где q = 1-p

34. Дискретные случайные величины. Таблица распределения вероятностей. Матиматическое ожидание и его свойства. Рассмотрим случайную величину * , возможные значения которой образуют конечную или бесконечную последовательность чисел x1, x2, ..., xn, ... . Пусть задана функция p(x), значение которой в каждой точке x=xi (i=1,2, ...) равно вероятности того, что величина примет значение xi

Такая случайная величина называется дискретной (прерывной). Функция р(х) называется законом распределения вероятностей случайной величины, или кратко, законом распределения. Эта функция определена в точках последовательности x1, x2, ..., xn, ... . Так как в каждом из испытаний случайная величина принимает всегда какое-либо значение из области ее изменения, то

 1°. Математическое ожидание постоянной С равно этой постоянной.    Доказательство. Постоянную C можно рассматривать как случайную величину , которая может принимать только одно значение C c вероятностью равной единице. Поэтому  2°. Постоянный множитель можно выносить за знак математического ожидания, т.е.

 3°. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий этих величин:

(41)

4°. Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий этих величин **:

35. Дисперсия дискретной случайной величины и ее свойства. Среднее квадратичное отклонение, коэффициент вариации. Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математичекого ожидания *:    Пусть - дискретная случайная величина, принимающая значения x₁, x₂, ..., x_n соответственно с вероятностями p₁, p₂, ..., p_n. Очевидно, случайная величина принимает значения с теми же вероятностями p₁, p₂, ..., p_n. Следовательно, согласно определению математического ожидания дискретной случайной величины, имеем    Если же - случайная величина с плотностью распределения , то по определению    Принимая во внимание определение дисперсии и свойства математического ожидания, имеем    Так как и - постоянные, то используя свойства математического ожидания, получим  Следовательно,    Откуда окончательно находим    Рассмотрим теперь свойства дисперсии.    1°. Дисперсия постоянной равна нулю. (Доказательство)    2°. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:    3°. Если и - независимые случайные величины , то дисперсия суммы этих величин равна сумме их дисперсий: Средним квадратическим отклонением случайной величины называется корень квадратный из ее дисперсии:

36. Биномиальный закон распределения и его числовые характеристики. Событие “n испытаний привели m раз к успеху” содержит столько элементарных событий, сколькими способами можно распределить m символов по n местам, что совпадает с числом сочетаний  из n элементов по m. Другими словами, пространство элементарных событий состоит из  точек, каждая из которых, по определению, имеет вероятность .

Следовательно, вероятность m успехов ( ) в серии из n испытаний Бернулли описывается формулой  , где p – вероятность успеха;  q – вероятность неудачи в одном испытании (q = 1 – р). Согласно существующей терминологии, число успехов в серии из n испытаний является случайной величиной, а формула (*) описывает распределение этой случайной величины и называется биномиальным законом распределения вероятности. Заметим, что выражение  представляет собой m-ый член биномиального разложения . Следовательно, , как того и требует понятие вероятности.

37. Распределение Пуассона и его числовые характеристики. Приближенная формула Пуассона. Пусть производится п независимых испытаний, в которых появление события А имеет вероятность р. Если число испытаний п достаточно велико, а вероятность появления события А в каждом испытании мало (p£0,1), то для нахождения вероятности появления события А k раз находится следующим образом. Сделаем важное допущение – произведение пр сохраняет постоянное значение: Практически это допущение означает, что среднее число появления события в различных сериях испытаний (при разном п) остается неизменным. По формуле Бернулли получаем: Найдем предел этой вероятности при п®