Тема 1.2. Анализ данных методами многомерной классификации.

1. Общая характеристика методов классификации многомерных данных.

2. Основные понятия кластерного анализа.

3. Иерархические методы кластеризации. Построение дендрограмм.

4. Итерационные методы кластеризации. Метод k-средних.

1. Общая характеристика методов классификации многомерных данных.

В 60-х годах XX века внутри прикладной статистики достаточно четко оформилась область, посвященная методам классификации. Среди наиболее распространенных отметим следующие: дискриминантный анализ, кластерный анализ, группировка.

При проведении дискриминантного анализа классы предполагаются заданными - плотностями вероятностей или обучающими выборками. Задача состоит в том, чтобы вновь поступающий объект отнести в один из этих классов. У понятия «дискриминация» имеется много синонимов: диагностика, распознавание образов с учителем, автоматическая классификация с учителем, статистическая классификация и т.д.

При кластеризации и группировке целью является выделение классов. Синонимы: построение классификации, распознавание образов без учителя, автоматическая классификация без учителя, типология, таксономия и др.

С помощью кластерного анализа (cluster) по эмпирическим данным производиться оценка, насколько элементы "группируются" в изолированные "скопления" или "кластеры". В кластерном анализе осуществляется естественное выявление классов, свободное от субъективизма исследователя. В результате имеем группы однородных объектов, сходных между собой при резком отличии этих групп друг от друга.

При группировке, наоборот, элементы разбиваются на группы независимо от того, естественны ли границы разбиения. Задача по-прежнему состоит в выявлении групп однородных объектов, сходных между собой (как в кластер-анализе), однако «соседние» группы могут не иметь резких различий (в отличие от кластер-анализа). Границы между группами условны, не являются естественными, зависят от субъективизма исследователя.

Главное назначение кластерного анализа – разбиение множества исследуемых объектов и их признаков на однородные в соответствующем понимании группы или кластеры. Это означает, что решается задача классификации данных и выявления соответствующей структуры в ней. Методы кластерного анализа применяются для различных случаев, в том числе, и когда речь идет о простой группировке, в которой все сводится к образованию групп по количественному сходству.

Большое достоинство кластерного анализа в том, что он позволяет проводить разбиение объектов не только по одному параметру, но и по целому набору признаков. Кроме того, кластерный анализ в отличие от многих методов математической статистики не накладывает никаких ограничений на вид рассматриваемых объектов, и позволяет рассматривать множество исходных данных практически любой природы. Это имеет большое значение, например, для прогнозирования конъюнктуры, когда показатели имеют разнообразный вид, затрудняющий применение традиционных эконометрических подходов.

Основные понятия кластерного анализа.

Основными понятиями кластерного анализа являются понятия «объект» и «признак».

Количество объектов кластеризации обычно называют объемом выборки.

Признак (свойство, переменная, характеристика) представляет собой конкретное свойство объекта, которое может выражаться как числовыми, так и не числовыми значениями.

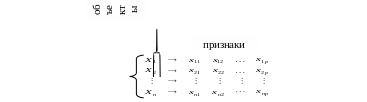
Матрица "Объект-признак" представляет собой прямоугольную таблицу, состоящую из значений признаков, описывающих свойства исследуемой выборки наблюдений. Одно наблюдение будет записываться в виде отдельной строки, состоящей из значений используемых признаков. Отдельный же признак в такой матрице данных будет представлен столбцом, состоящим из значений этого признака по всем объектам выборки.

Задача кластерного анализа заключается в том, чтобы на основании имеющихся признаков выделить в соответствии с заданными критериями требуемое количество кластеров:

где Х_і - i-тое подмножество, выделенное из общего множества объектов Х (і-тый кластер).

Кластер можно охарактеризовать как группу объектов, имеющих общие свойства.

Характеристиками кластера можно назвать два признака:

• внутренняя однородность;

• внешняя изолированность.

Примечание. Наибольшее применение кластеризация первоначально получила в таких науках как биология, антропология, психология. Для решения экономических задач кластеризация длительное время мало использовалась из-за специфики экономических данных и явлений.

В качестве критерия оптимальности кластеризации часто используется внутригрупповая сумма квадратов отклонений от среднего:

→ min (1)

где x_i - представляет собой измерение i-го объекта.

В кластерном анализе разбиению на кластеры при разных значениях исходных данных предварительно осуществляется нормировка (стандартизация) данных:

(2)

где х_ik – значение k-того признака і-того объекта;

– выборочное среднее:

(3)

S_x – среднеквадратическое отклонение:

(4)

Кластер статистически определяется, как совокупность точек, лежащих на расстоянии не больше, чем r от некоторого "центра тяжести" в m-мерном пространстве. Отсюда для решения задачи кластерного анализа необходимо определить метрику или функцию расстояния между объектами.

Расстояние между объектами (метрика расстояний) отражает меру сходства, близости объектов между объектами по всей совокупности используемых признаков.

Формально расстоянием между объектами в пространстве признаков называется такая величина d_ij , которая удовлетворяет следующим аксиомам:

1. d_ij > 0 (неотрицательность расстояния);

2. d_ij = d_ji (симметрия);

3. d_ij + d_jk > d_ik (неравенство треугольника);

4. Если d_ij не равно 0, то i не равно j (различимость нетождественных объектов);

5. Если d_ij = 0, то i = j (неразличимость тождественных объектов).

Наиболее часто употребляются следующие функции (метрики) расстояний:

1) Евклидово расстояние (Euclidean distance)- наиболее общий тип расстояния. Оно является геометрическим расстоянием в многомерном пространстве:

d_ij= 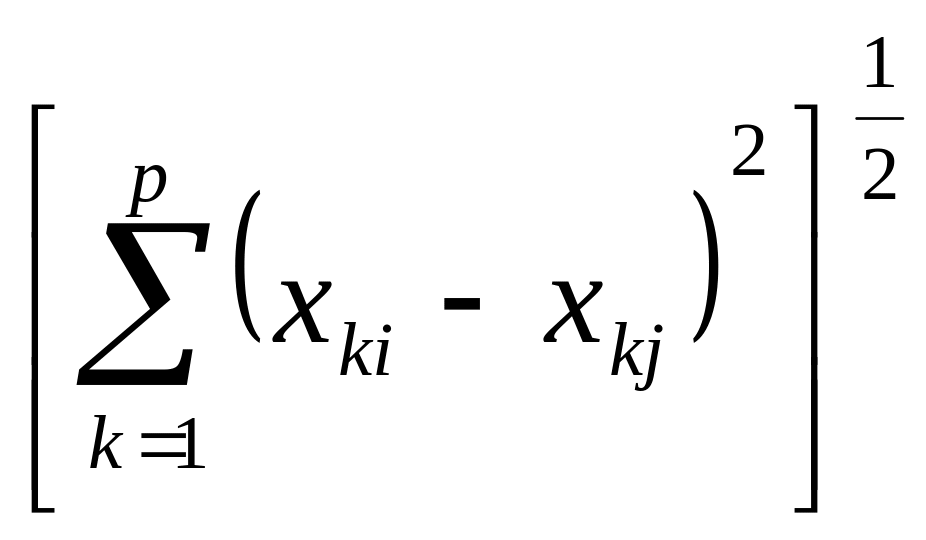(5)

где d_ij - расстояние между i-тым и j-тым объектами;

x_ki - численное значение k-того признака для i-того объекта;

x_kj - численное значение k-того признака для j-того объекта;

р - количество признаков, которыми описываются объекты.

2) Обобщенное степенное расстояние Минковского, выбор значения показателя "l" производится самим исследователем:

d_ij= (6)

3) Манхэттенское расстояние ("расстояние городских кварталов") - частный случай расстояния Минковского (наиболее легкое для вычислений):

d_ij= (7)

Расстояние между парами объектов d_ij могут быть представлены в виде симметричной матрицы расстояний:

Компоненты матрицы D могут быть рассчитаны с использованием любой из перечисленных выше формул метрики расстояний.

В результате применения различных методов кластеризации могут быть получены неодинаковые результаты, это нормально и является особенностью работы того или иного алгоритма. Данные особенности следует учитывать при выборе метода кластеризации.

Наибольшее распространение в популярных статистических пакетах получили два группы методов кластерного анализа: иерархические методы и итеративные методы.

Иерархические методы кластеризации. Построение дендрограмм.

Иерархические методы кластерного анализа используются при небольших объемах наборов данных. Преимуществом иерархических методов кластеризации является их наглядность.

Иерархические алгоритмы связаны с построением дендрограмм (от греческого dendron – «дерево»), которые являются результатом иерархического кластерного анализа.

Дендрограмма (dendrogram) ‑ древовидная диаграмма, содержащая n уровней, каждый из которых соответствует одному из шагов процесса последовательного укрупнения кластеров.

Иерархические методы кластеризации делятся на две группы:

а) дивизимные (делимые), в которых число кластеров возрастает, начиная с одного, в результате чего образуется последовательность расщепляющих групп;

б) агломеративные, характеризуемые последовательным объединением исходных элементов и соответствующим уменьшением числа кластеров.

Принцип работы описанных выше групп методов в виде дендрограммы показан на рисунке 1.

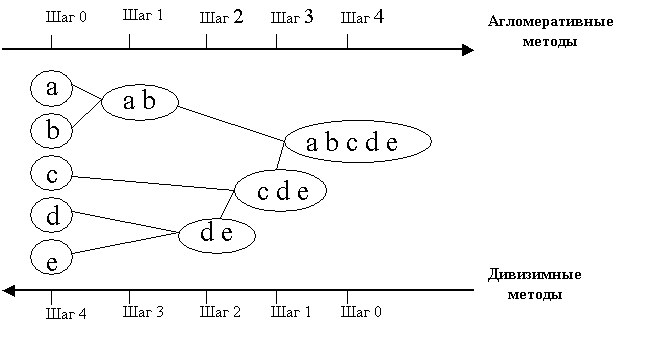
Рисунок 1 ‑ Дендрограмма агломеративных и дивизимных методов

Существует много способов построения дендограмм. Рассмотрим один из них на примере иерархического агломеративного метода.

Иерархические агломеративные методы — это многошаговые методы классификации, работающие по следующему алгоритму:

1) На нулевом шаге каждый объект считается отдельным кластером, т.е., за разбиение принимается исходная совокупность n элементарных кластеров, матрица расстояний между которыми (pij) = (dij).

2) На каждом следующем шаге происходит:

• объединение двух кластеров Xs и Xt, сформированных на предыдущем шаге, в один кластер:

, при этом размерность матрицы расстояний D уменьшается по сравнению с ее размерностью на предыдущем шаге на единицу;

• определение расстояния от этого класса до всех остальных объектов. pi,s⊕t - расстояние между кластерами Xi (объектами) и Xs⊕t (i≠s, i≠t), которое можно рассчитать, используя соответствующую методу формулу расстояния между кластерами (см. п. 2 лекции).

3) Процедура повторяется, пока все объекты не объединятся в один класс. Результат работы иерархического метода представляет собой дендрограмму - графическое изображение результатов процесса последовательной кластеризации, которая осуществляется в терминах матрицы расстояний.

Пример. Пусть имеется информация по объемам продаж в пяти магазинах небольшой розничной сети, торгующей холодильниками и стиральными машинами: (4; 3), (7; 4), (2; 0), (2; 1), (0; 4).

Первая координата соответствует продажам холодильников в магазине за неделю, а вторая координата — продажам стиральных машин.

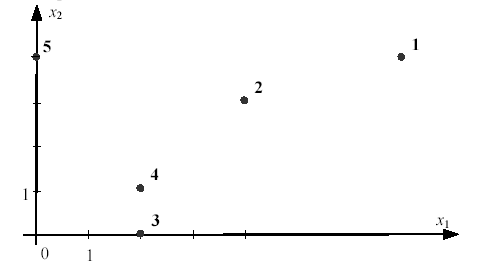
За метрику расстояний примем квадрат евклидова расстояния. Получим следующую матрицу расстояний:

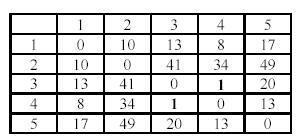
Метод ближнего соседа. Начальное разбиение таково: {1, 2, 3, 4, 5}.

Минимальное расстояние между кластерами ρ3,4=1, поэтому переходим к следующему разбиению: {1, 2, 3 4 , 5}.

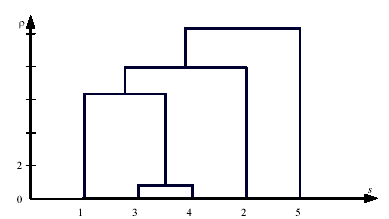
Последовательность разбиений представлена в таблицах.

{1, 2, 3, 4, 5} →{1, 2, 3 4, 5} →{1 (3 4), 2, 5}→

→ {1 (3 4) 2, 5} →{1 2 3 4 5}

На рисунке изображена соответствующая дендрограмма (слева проставлены расстояния, при которых происходит переход к новому разбиению).