Рубежный тестовый контроль

1. Численные методы поиска локального минимума (максимума) функций применяются для того, чтобы

   1. эта задача решалась с любой наперед заданной точностью;

   2. решить поставленную задачу за минимальное время;

   3. иметь возможность решать поставленную задачу как для локального, так и для глобального минимума (максимума);

   4. избежать математических трудностей, связанных с применением необходимого и достаточного условий.

2. Унимодальной называется функция, которая

   1. слева и справа от точки минимума возрастает;

   2. является монотонной по обе стороны от точки экстремума;

   3. является монотонной на рассматриваемом интервале ;

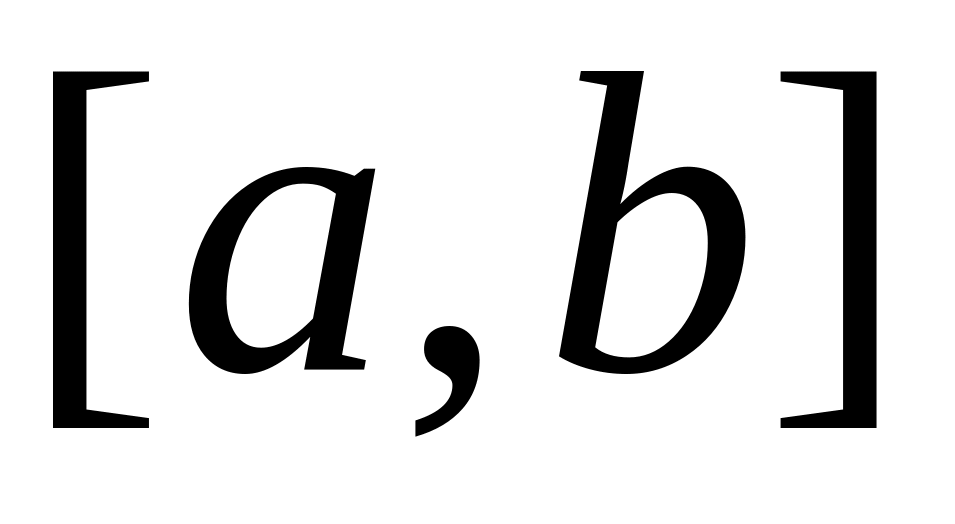   4. монотонно убывает слева и монотонно возрастает справа от точки минимума.

3. Метод дихотомии

   1. позволяет отыскивать только минимум функций;

   2. позволяет отыскивать как минимум, так и максимум функций на заданном интервале;

   3. решает задачу отыскания минимума унимодальных функций путем сравнения значений функций в двух произвольных точках отрезка;

   4. оперирует значениями унимодальной функции, взятыми в двух точках, лежащих симметрично от середины исследуемого отрезка.

4. Метод золотого сечения

   1. позволяет отыскать локальный минимум унимодальной функции;

   2. является численным методом отыскания как минимума, так и максимума функции на заданном отрезке [a,b];

   3. путем сравнения двух значений функции на исследуемом отрезке определяет минимальные значения функции;

   4. основан на использовании «золотой» пропорции.

5. Метод дихотомии по сравнению с методом золотого сечения

   1. более предпочтителен с точки зрения минимума вычислительных циклов;

   2. более экономичен по общему количеству команд;

   3. требует меньших затрат машинного времени в силу своей специфики;

   4. позволяет решать задачу минимизации со сколь угодной степенью точности.

1.4. Оптимизационная задача при отсутствии ограничений. Целевые функции нескольких переменных

Основные понятия. Дадим определения положительно определенной, отрицательно определенной и неопределенной матриц.

Рассмотрим симметрическую матрицу Q. В такой матрице n строк, n столбцов и она такова, что , где T – символ транспонирования.

Диагональными элементами – матрицы называются такие ее элементы, у которых номера строк и столбцов совпадают.

Диагональным минором k-го порядка матрицы Q называется определитель, соответствующий таким элементам матрицы Q, которые остаются после вычеркивания в ней последних n-k строк и столбцов. Например, в матрице

диагональными минорами первого, второго и третьего порядков соответственно являются определители

, , .

Матрица Q называется положительно определенной, если у этой матрицы все диагональные элементы и диагональные миноры положительны.

Пример. Рассмотрим матрицу

.

В этой матрице диагональные элементы 1, 2 и 3 положительны, диагональные миноры

, ,

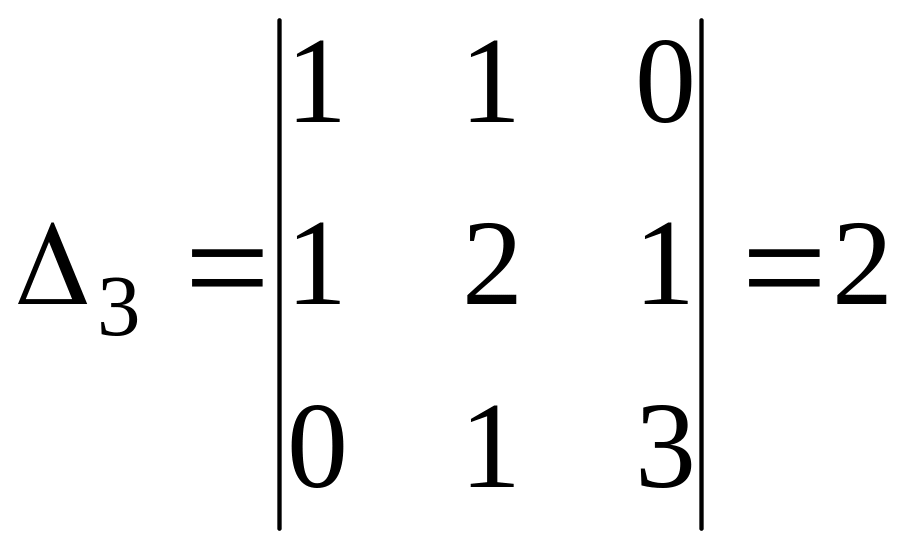
так же положительны. Матрица Q положительно определенная.

Матрица Q называется отрицательно определенной, если у этой матрицы диагональные элементы отрицательны, а диагональные миноры имеют чередующийся знак, т.е. .

Пример. Рассмотрим матрицу

.

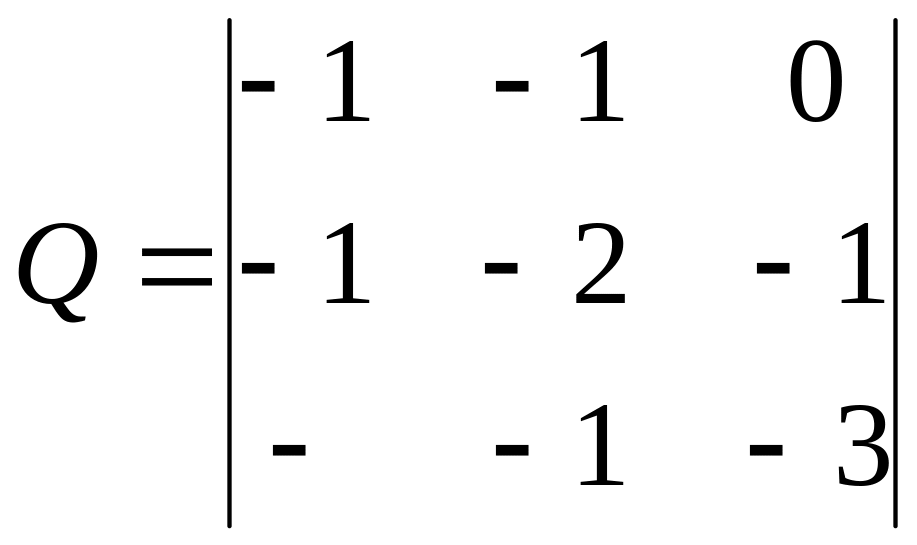В этой матрице диагональные элементы отрицательны. Диагональные миноры , , . Матрица Q – отрицательно определенная.

Матрица называется неопределенной, если у этой матрицы имеются признаки как положительно, так и отрицательно определенной матрицы.

Пример. Рассмотрим матрицу

.

В этой матрице один диагональный элемент отрицательный, а остальные положительные. Матрица Q – неопределенная.

Постановка и решение задачи

Пусть задана скалярная функция

, ,

где – неограниченное n-мерное пространство вещественных чисел, x – точка с координатами , …, , а f(x) имеет все производные ; . Требуется найти такую точку ), в которой функция f(x) достигает локального минимума или максимума.

Такую задачу назовем идеальной, т.к. в практических задачах область возможных значений аргумента x ограниченная, а функция f(x) в отдельных точках может не иметь производных даже и первого порядка. Тем не менее решение такой задачи мы все же рассмотрим.

Получим необходимые и достаточные условия локального минимума функции f(x).

Пусть – некоторая точка пространства . Согласно формуле Тейлора [1]

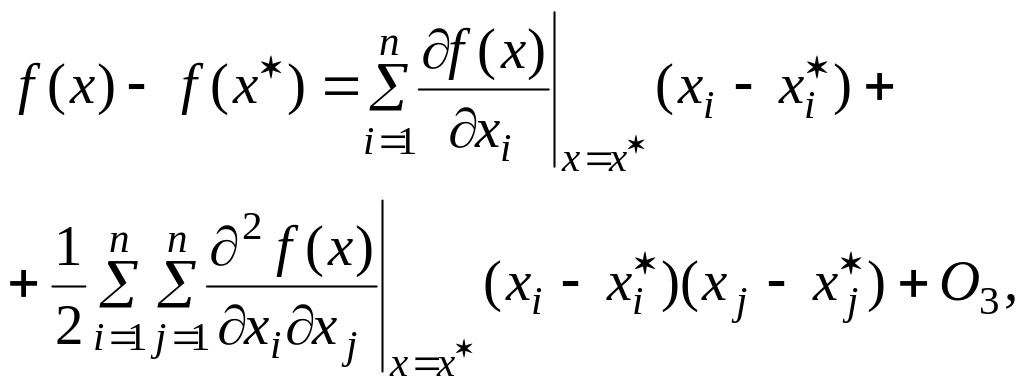(1.86)

где – слагаемые более высокого порядка по отношению к множителям .

Вводя в рассмотрение вектор

, (1.87)

где , , – проекции (компоненты) вектора , (1.86) перепишем в виде

. (1.88)

В этом выражении вектор

и – матрица (матрица Гессе)

(1.89)

Анализируя правую часть выражения (1.88) так же, как это делалось для функции одного переменного, приходим к следующему заключению.

Для наличия в точке локального минимума необходимо, чтобы

, (1.90)

и достаточно, чтобы матрица Гессе была положительно определенной.

Для наличия в точке локального максимума необходимо, чтобы

, (1.91)

и достаточно, чтобы матрица Гессе была отрицательно определенной.

Если в точке матрица Гессе является неопределенной, то – седловая точка.

Учитывая выражение (1.87), необходимые условия (1.90), (1.91) запишем в следующем виде

, . (1.92)

Как же практически нужно действовать при отыскании точки , в которой функция достигает локального минимума или максимума?

Во-первых, необходимо разрешить n уравнений (1.92) относительно x. Тем самым будут найдены n координат точки . Во-вторых, в точке исследуется матрица Н (1.89) на знакоопределенность. Так, если матрица окажется положительно определенной, то в точке – локальный минимум, если окажется отрицательно определенной, то в точке – локальный максимум, если неопределенная, то в отсутствует как минимум, так и максимум.

Замечание 1. Точки минимума или максимума, найденные рассмотренным выше способом, назовем точками экстремума.

Замечание 2. Если функция f(x) дважды непрерывно дифференцируема, то .

Рассмотрим частные случаи.

1. Пусть 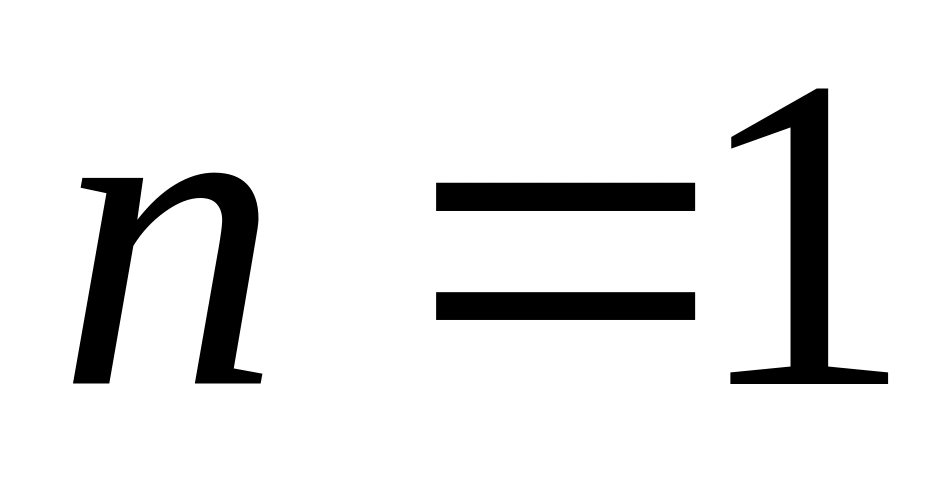, . В таком случае

,

.

При 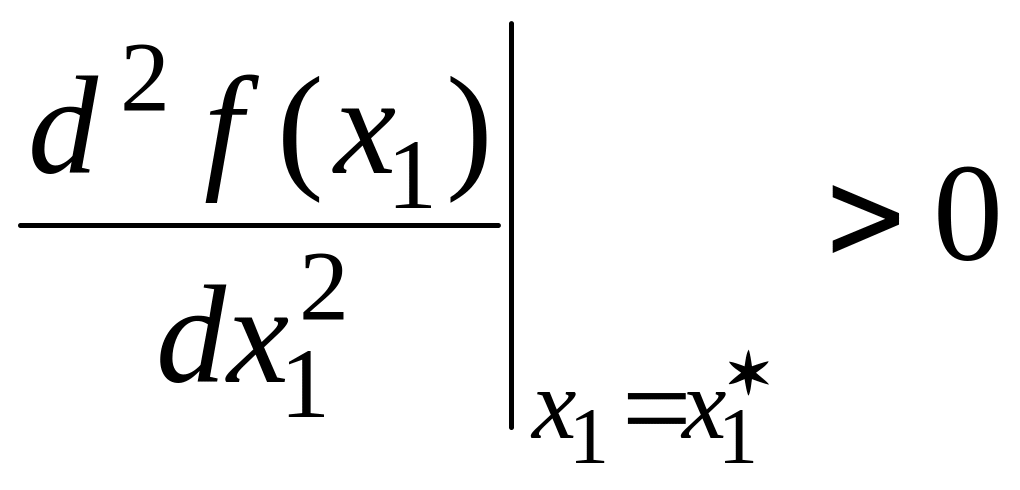– минимум, при 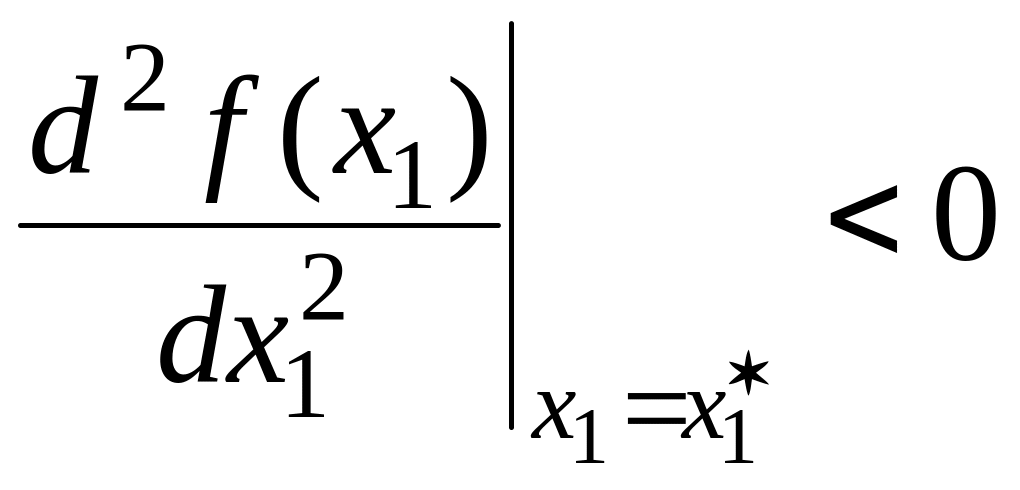– максимум.

2. Пусть , , тогда

;

.

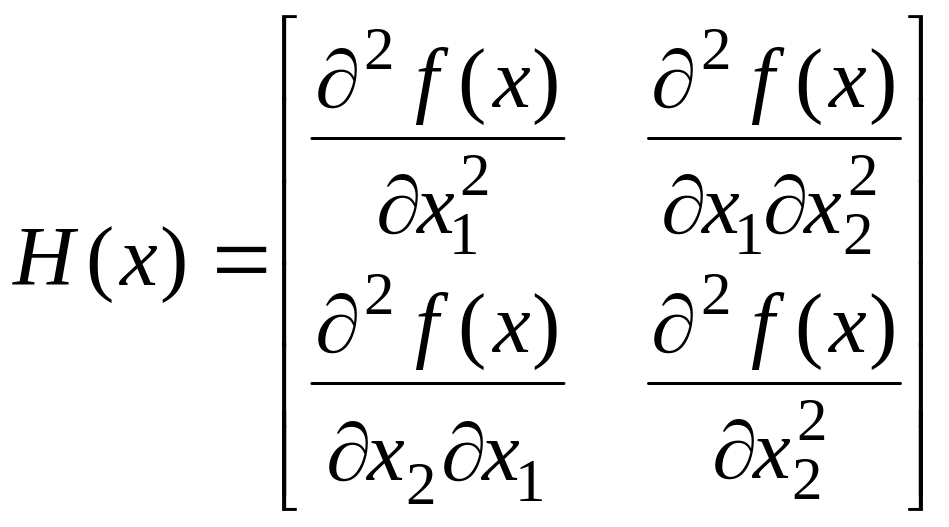Если в точке

то

– точка минимума; если в этой же точке

то

- точка максимума.

Пример. Исследовать на экстремум функцию

.

Записываем необходимое условие экстремума:

(1.93)

Система (1.93) имеет два решения:

I: ;

II: .

Далее

. (1.94)

Решению II отвечает матрица (1.94)

.

Эта матрица отрицательно определенная, следовательно, в точке имеет место максимум. Решению II отвечает матрица (1.94)

.

Эта матрица неопределенная, следовательно, точка с координатами – седловая точка.

Задача перевозки сыпучего материала. Требуется перевезти сыпучий материал объема с одного места на другое. Перевозку предполагается осуществить контейнером, который еще предстоит изготовить. Контейнер должен быть таким, чтобы затраты на его изготовление и перевозку груза этим контейнером были минимальными.

Р ассмотрим один из простейших вариантов этой задачи, когда контейнер имеет форму параллелепипеда с размерами основания и высотой h, рис. 1.21.

Объем контейнера

,

стоимость его изготовления

,

где с_о, с_к, с_с – стоимость изготовления одного м² соответственно основания, крышки и стенок контейнера.

Общие расходы на изготовление контейнера и перевозку груза

, (1.95)

где с₁, – стоимость одного рейса (туда и обратно). Целевая функция S (1.95) содержит три параметра а, b, h, которые подлежат определению. Найдем такие значения параметров а, b, h, чтобы целевая функция S (1.95) достигала минимума.

Необходимые условия экстремума (1.92) запишутся в виде

;

;

.

Эти уравнения разрешаются (выкладки опущены):

;

,

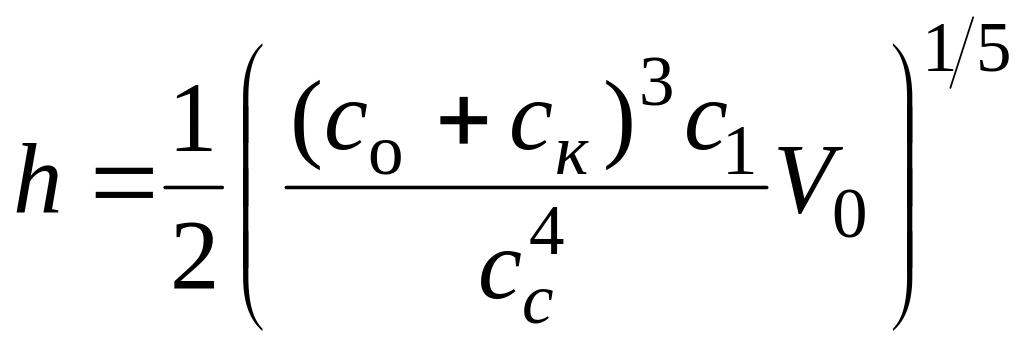при этом объем контейнера

.

Найденные значения параметров а, b, h следует использовать при исследовании матрицы Гессе

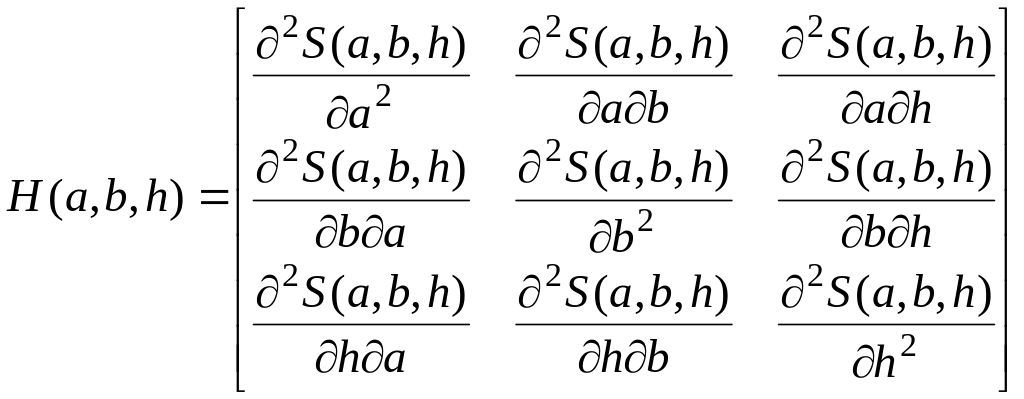(1.97)

на знакоопределенность. Если поставленная задача имеет решение, будет положительно определенной.

Заметим, что в зависимости от обстоятельств, один из трех конструктивных параметров а, b, h или любая пара из них могут быть фиксированными (например, в случае ограничений по габаритам). В таких случаях определению подлежат не три, а два или даже один параметр.