Градиентный подход поиска локального минимума функции нескольких переменных
Пусть требуется
отыскать такую точку
в которой целевая функция
достигает локального минимума.
Д
опустим,
что
– заданный исходный вектор и
– антиградиент функции y(x),
соответствующий вектору
рис. 1.25.
Вектор
выберем так, что
,
, (1.98)
где
– некоторая неотрицательная константа,
которая регулирует величину шага в
направлении антиградиента
.
В скалярной форме выражение (1.98) записывается в виде
;
. . . . . . . . . . . . . . . . . . . (1.99)
.
Д
опустим,
что константа
задана, тогда имеется возможность c
помощью соотношения (1.98) построить
некоторую последовательность точек
,
которая, вообще говоря, может привести
к точке минимума
,
рис. 1.26. На этом рисунке с помощью линий
уровня воссоздается рельеф целевой
функции
.
Задавая константу
,
следует помнить, что при малых
процесс продвижения от точки
в окрестность точки
будет весьма медленным, а при больших
имеется опасность получить неустойчивую
последовательность точек
.
Замечание. Компоненты градиента можно находить численными методами, вычисляя их, например, по следующим формулам (n=2)
;
,
где
и
– некоторые малые приращения, k
– номер итерации.
Процесс вычислений заканчивается, как только
,
где
– некоторое малое число, т.е. вычисление
прекращается в том случае, когда
расстояние точки
от точки
станет меньше наперед заданного числа
.
Пример.
Пусть
,
.
Тогда
.
Зададим
.
В таком случае, согласно (1.99) на первом
шаге поиска
имеем:
;
,
т.е.
;
.
При k = 2
;
,
т.е.
;
и т.д. Заметить,
что
,
при
,
что и должно быть, т.к. целевая функция
в начале координат имеет локальный
минимум.
Если вместо
взять
,
то получим расходящуюся последовательность
точек
,…
.
Рассмотрим некоторые разновидности градиентного метода.
Метод наискорейшего спуска
Переход от предыдущей точки к последующей по методу наискорейшего спуска осуществляется так, что
,
. (1.100)
В этом выражении
константа
на каждом шаге (переход от
к
)
выбирается так, чтобы целевая функция
в направлении
антиградиента достигла минимума
(произойти это должно в точке
).
В частности, требуемое значение
можно найти, как решение уравнения
. (1.101)
В координатной форме векторному уравнению (1.100) соответствует система уравнений
,
. (1.102)
Покажем, что векторы
,
– ортогональны. Действительно, в точке
целевая функция
,
где для
имеют место выражения (1.102). В таком
случае согласно (1.101)
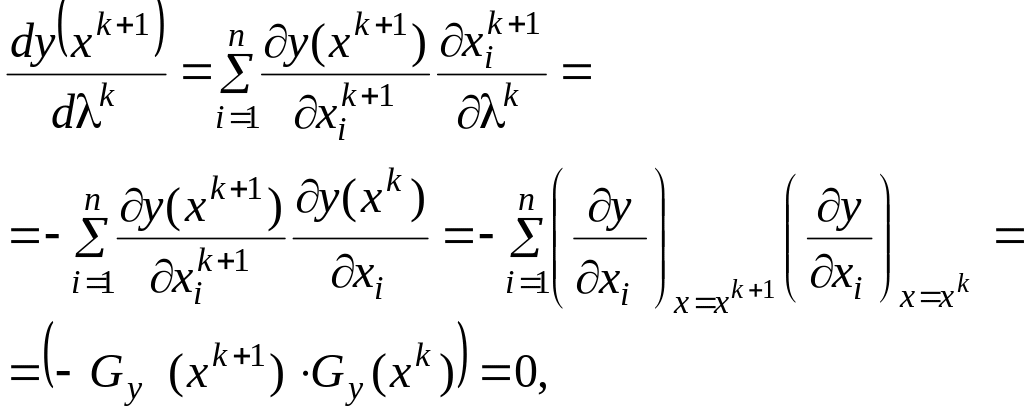
а это означает,
что
.
Рассмотрим геометрическую интерпретацию метода наискорейшего спуска.
П
усть
целевая функция
имеет такой рельеф, как это с помощью
линий уровня показано на рис. 1.27. На этом
рисунке воспроизводится траектория
поиска точки
.
Пример. Пусть
,
.
Как и в предыдущем примере
.
k =0: Согласно (1.102)
,
. (1.103)
В таком случае целевая функция
.
(1.104)
Уравнение (1.101) запишется как
.
Заметим, что
найденное значение
обеспечивает целевой функции (1.104)
минимум в силу положительности второй
производной:
.
Согласно (1.103), при
,
.
Точка минимума достигнута за один шаг. Правда, так бывает далеко не всегда.
Заметим в заключение,
что оптимальное значение
на каждом шаге для функции
может быть найдено одним из численных
методов – дихотомии, золотого сечения
и т.п.