6 Цепи с распределёнными параметрами

В цепях с распределенными параметрами (ЦРП) индуктивности, емкости и активные сопротивления распределены по длине. Ток и напряжение в любой точке цепи являются функциями времени t и пространственных координат ( напр. длины).

Цепи с распределенными параметрами, выполненные в виде двухпроводных линий, называются длинными линиями, если длина

превышает длину волны питающего тока.

Целью изучения длинных линий является анализ распределений токов и напряжений вдоль линии. Особенности этих распределений определяют применение длинных линий в качестве питающих линий для токов высокой частоты (так называемых фидеров), колебательных контуров, фильтров, металлических изоляторов, трансформаторов сопротивлений, линий задержки, элементов формирователей импульсов и т.д.

Электрические свойства длинной линии характеризуются первичными параметрами: активное сопротивление единицы длинны линии R₁[O_м/м]-погонное сопротивление; погонная емкость С₁[Ф/м]; погонная проводимость изоляции G₁[С_м/м] (утечка) => погонные параметры Д.Л.

1) Дифференциальные уравнения напряжения и тока в длинной линии

где: М - любая точка линии; х - текущая координата;

Напряжение и ток в любой точке линии в произвольный момент времени можно определить с помощью дифференциального уравнений. Эти уравнения связывают изменения токов и напряжений вдоль линии с изменением их во времени. Опуская вывод этих уравнений, запишем их в окончательном виде:

(6.1)

Эти уравнения позволяют определить ток и напряжение в любой точке линии в любой момент времени и называются телеграфными уравнениями.

6.1.1 Решение телеграфных уравнений для линий без потерь Для того, чтобы раскрыть физические процессы в длинной линии, рассмотрим линию без потерь: R₁= 0; G₁= 0

Тогда телеграфные уравнения принимают вид:

(6.2) (6.3)

Продифференцируем обе части уравнения (6.2) по х, а обе части уравнения (6.3) по t. Получим:

(6.4) (6.5)

Подставляя (6.5) в (6.4), получим:

(6.6) Аналогично для тока:

(6.7)

Уравнения (6.6) и (6.7) называются волновыми уравнениями для напряжения и тока в линии.

Уравнение (6.6) можно записать в следующем виде:

(6.8)

Где скорость распространения волны в линии.

Общий вид решения волновых уравнений:

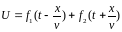(6.9)

(6.10)

Здесь f₁, f₂, ψ_1, ψ₂ - функции, определяемые конкретными условиями задачи (частные решения).

Первое слагаемое в (6.9) f₁(t + x/v) представляет собой волну напряжения, распространяющуюся по линии вдоль оси X со скоростью v (прямая волна). Функция f₂(t + x/v) определяет волну, которая распространяется по линии в противоположном направлении (обратная волна). Соответственно, функции ψ₁(t+ x/v) и ψ₂(t + x/v) представляют собой прямую и обратную волны тока. Прямая волна несёт энергию от генератора к нагрузке, обратная волна несёт энергию от нагрузки к генератору. Необходимым условием существования обратной волны является условие отражения на конце линии. Режим, при котором отражение отсутствует, называется режимом бегущих волн. Напряжение и ток в линии связаны между собой следующим образом:

Где U_пр,i_пр - напряжение и ток прямой волны; U_o6p,i_o6p - напряжение и ток обратной волны; z₀ - волновое сопротивление линии.

Будем считать, что в линии распространяется только прямая волна. Если функция напряжения в точке х = 0 равна f₁(t,0) = U*cosωt, то напряжение и ток в произвольной точке х линии будут представлены выражениями:

(6.11)

U(x) = U • cosω(t - x/v) = U • cos(ωt - βх)

i(x) = I • cosω(t - x/v) = I • cos(ωt - βх)

где U- амплитуда напряжения прямой волны; I- амплитуда тока прямой волны; β= ω/v - волновое число или коэффициент фазы, который характеризует количественное изменение фазы на участке линии. Так как ω = 2πf; λ = v/f ,то β = 2π /λ.

(исправить фазу третьей кривой)

Рисунок 6.3 - Распространение волны напряжения в линии без потерь

Уравнение (6.11) представляет собой решение телеграфных уравнений для линии без потерь.

Расстояние, на котором фаза напряжения или тока меняется на 2л, соответствует длине волны. Поэтому волновое число определяется соотношением:

β = 2π /λ.

По мере распространения волны любая точка с фиксированной фазой перемещается вдоль линии со скоростью v, называемой фазовой скоростью. За время Т = 1/f точка перемещается на расстояние, равное длине волны:

то есть при заданной частоте колебаний длина волны является функцией погонных параметров L₁ и C₁ .