№50

Ряд Фурье для четных и нечетных функций.

Л.1: Если f(x)— четная функция на [-a;a] то . Если f(x) — нечетная функция на

Для четных функций

Для нечетной функции доказательство аналогично Л.2: Произведение двух четных или двух нечетных функций есть четная функция, четной и нечетной — нечетная функция - четные функции

Остальное доказывается аналогично. С помощью лемм 1, 2 получаем следующие коэффициенты Фурье: — для четной функции: — для нечетной функции: . Таким образом, ряд Фурье для четной функции , для нечетной функции

Пример: Разложить в ряд Фурье функцию с периодом 2π, если на [-π;π] она имеет вид

Решение:

Данная функция является четной (рис. 1). Поэтому

Рисунок1

№51

Ряд Фурье для непериодических функций. Разложение в ряд Фурье в интервале [−l, l] .

Рассмотрим кусочно-непрерывную f (x), заданную в интервале [− L, L]. Используя подстановку , преобразуем ее в функцию определенную и интегрируемую в интервале [−π, π]. Разложение в ряд Фурье для функции F (y) имеет вид Коэффициенты Фурье для данной функции определяются формулами

Возвращаясь к первоначальным переменным, то есть полагая , получим следующие выражения для ряда Фурье исходной функции f (x): где

Разложение в ряд Фурье в интервале [a,b]

Если функция f (x) определена в интервале [a,b], то ее разложение в ряд Фурье определяется той же самой формулой где , а коэффициенты вычисляются следующим образом:

№52

Ряд Фурье для функций с периодом 2l.

Пусть f(x) - четная функция с периодом 2L, удовлетворяющая условию f(-x) = f(x) .

Тогда для коэффициентов ее ряда Фурье находим формулы:

=

=

= 0, где n=1,2, ...

Таким образом, в ряде Фурье для четной функции отсутствуют члены с синусами, и ряд Фурье для четной функции с периодом 2L выглядит так:

Пусть теперь f(x) - нечетная функция с периодом 2L, удовлетворяющая условию f(-x) = - f(x). Тогда для коэффициентов ее ряда Фурье находим формулы: , где n=1,2, ...

Таким образом, в ряде Фурье для нечетной функции отсутствует свободный член и члены с косинусами, и ряд Фурье для нечетной функции с периодом 2L выглядит так: .

Если функция f(x) разлагается в тригонометрический ряд Фурье на промежутке , то , где , , .

Если f(x) разлагается в тригонометрический ряд Фурье на [0,L], то доопределив заданную функцию f(x) соответствующим образом на [-L,0]; далее периодически продолжив на (T=2L), получим новую функцию, которую разлагаем в тригонометрический ряд Фурье.

Для разложения в ряд Фурье непериодической функции, заданной на конечном произвольном промежутке [a,b], надо : доопределить на [b,a+2L] и периодически продолжить, либо доопределить на [b-2L,a] и периодически продолжить.

№53

Ряд Фурье в комплексной форме.

экспонента от чисто мнимого аргумента определяется равенством . Отсюда немедленно вытекают формулы Эйлера справедливые для всех вещественных чисел . Предполагая, что функция f разлагается в ряд Фурье, заменим в нем синусы и косинусы по формулам Эйлера:

где использованы обозначения

Вновь используя формулы Эйлера, преобразуем выражения для коэффициентов :

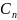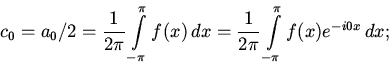
Итак, мы видим, что для всех значений n коэффициенты ищутся по одной формуле При этом имеет место разложение называемое комплексной формой ряда Фурье.

№54