4.1 Общие сведения

Цифровая обработка сигналов как направление развития науки и техники зародилась в 1950-х годах XX века и поначалу представляла собой экзотическую отрасль радиоэлектроники, практическая ценность которой была далеко не очевидной. Однако за прошедшие время благодаря успехам микроэлектроники системы цифровой обработки сигналов не только воплотились в реальность, но и вошли в повседневную жизнь. Более того, во многих прикладных областях цифровая обработка стала вытеснять традиционную аналоговую.

Сущность цифровой обработки состоит в том, что физический сигнал (напряжение, ток и т. д.) преобразуется в последовательность чисел, которая затем подвергается математическим преобразованиям в вычислительном устройстве. Трансформированный цифровой сигнал (последовательность чисел) при необходимости может быть преобразован обратно в напряжение или ток.

Любой непрерывный сигнал, ограниченный некоторыми предельными значениями, может быть дискретизирован по времени и по уровню (квантован).

Дискретизация – физическая операция преобразования непрерывной по времени величины в дискретную, при которой сохраняются ее мгновенные моменты времени (моменты дискретизации).

Квантование – физическая операция преобразования непрерывной по уровню величины в дискретную (квант), т.е. замена ее мгновенных значений цифровым кодом определенной разрядности.

Обработка и передача дискретной последовательности (информации) имеет ряд преимуществ по сравнению с информацией, заданной в непрерывном виде. Дискретные сигналы в меньшей степени подвержены искажениям в процессе передачи и хранения. Они легко преобразуются в двоичный код и обрабатываются с помощью ЭВМ.

Для простоты рассмотрим дискретизацию одномерных сигналов. Одномерные сигналы описываются вещественной или комплексной функцией x_a(t), определенной на интервале вещественной оси (обычно оси времени).

Аналоговые сигналы описываются непрерывной или кусочно-непрерывной функцией x_a(t), причем сама функция и аргумент t могут принимать любые значения на некоторых интервалах.

Для примера рассмотрим сигнал x_a(t)=Ae^-αt, где A=1, α>0, переменная α принимает вещественные значения. Временная форма сигнала x_a(t) показана на рис. 4.1.

Рис. 4.1

Дискретные сигналы описываются решетчатыми функциями (последовательностями) x(nT); где T = const – интервал дискретизации; n = 0, 1, 2,… Функция x(nT) может принимать в дискретные моменты времени nT произвольные значения на некотором интервале. Эти значения функции называются выборками или отсчетами функции. Последовательность может быть конечной и состоять из определенного количества отсчетов. Во многих случаях при обозначении дискретных последовательностей переменная T исключается из записи, т. е. x(nT) ≡ x_n. Пример дискретизации сигнала x_a(t) показан на рис. 4.2. Так как T = const, значения времени t на рис. 4.2 могут быть заменены значениями переменной n (рис. 4.3).

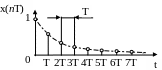
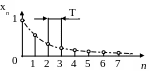
Рис. 4.2 Рис. 4.3

Цифровые сигналы – это квантованные по уровню дискретные сигналы. Они описываются квантованными решетчатыми функциями (квантованными последовательностями) x_ц(nT), принимающими в дискретные моменты времени nT лишь конечный ряд дискретных значений – уровней квантования h₁, h₂,…h_i,…, h_N. Пример оцифровки сигнала x_a(t) представлен на рис. 4.4.

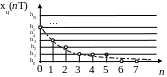
Рис. 4.4

Аналоговый сигнал можно дискретизировать с помощью амплитудно-импульсного импульсного элемента, реагирующего на дискретные равноотстоящие значения входного сигнала в моменты времени t=nT. Восстановление аналогового сигнала x_a(t) по его дискретному представлению (последовательности выборок x(nT)) сводится к использованию различных интерполирующих процедур.

Принцип дискретизации аналогового сигнала и его восстановления основан на теореме отсчетов академика В. А. Котельникова [28–30]. При выполнении определенных условий, определяемых теоремой Котельникова, операции дискретизации и восстановления взаимно обратны.

Если сигнал x_a(t) имеет ограниченный спектр x_a(jω), при этом x_a(jω) = 0 при |ω|> ω₀, то такой сигнал можно однозначно представить последовательностью выборок x(nT), n = 0, 1, 2,… при T= 2π/ ω_д, где ωд = 2π f_д ≥ 2 ω₀.

При этом

откуда следует, что сигнал x_a(t) можно получить, если пропустить последовательность x(nT) через идеальный (физически не реализуемый) аналоговый фильтр нижних частот с частотой среза ω_с = π/T и с амплитудно-частотной характеристикой |K(jω)| = T в полосе пропускания. Спектр последовательности x(nT), полученной в результате дискретизации x_a(t) с частотой ω_д = 2π/T равен сумме спектров сигнала x_a(t), смещенных по оси частот на все возможные значения частоты кратные частоте дискретизации.

Использование теоремы Котельникова встречает определенные трудности, связанные с тем, что допущение об ограниченности частотного спектра для реальных сигналов никогда не выполняется, т.к. любой ограниченный во времени непериодический сигнал всегда имеет бесконечный спектр. Поэтому определение верхней границы спектра ω₀ обычно производится приближенно (по критерию 90%-го содержания энергии или средней мощности сигнала). Иными словами, в качестве верхней границы спектра ω₀ принимают частоту, за пределами которой составляющие спектра достаточны малы по сравнению с его основными составляющими (например, подавлены на 80 дБ).

На практике частота дискретизации обычно превышает верхнюю частоту спектра сигнала в 3-5 раз. Частота равная половине частоты дискретизации носит название частоты Найквиста. Дискретизация и квантование сигнала осуществляется с помощью аналого-цифровых преобразователей (АЦП).

Как было рассмотрено ранее, цифровой сигнал представляет собой квантованный по уровню дискретный сигнал. Отличительной особенностью дискретизации по уровню является замена значений дискретного сигнала дискретной шкалой h1, h2,…, hN. При этом разность между уровнями кратна некоторому фиксированному значению, называемому шагом квантования Δ. Каждому уровню квантования дискретного сигнала ставится в соответствие определенный код, т. е. уровни квантования связываются с числами в выбранной системе счисления. Одна из наиболее часто используемых в технике является двоичная система счисления. Кроме того, в вычислительной технике широко используется восьмеричная и шестнадцатеричная системы счисления, так как 8 и 16 являются степенями числа 2. Используемые при кодировании числа могут иметь разные формы представления (с фиксированной или плавающей запятой). Числа могут быть положительными или отрицательными. В технике, как правило, используются числа с ограниченным количеством разрядов. Достаточно часто используется целочисленное кодирование уровней квантования сигнала.

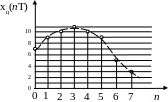
Рис. 4.5

В таблице 4.1 представлено кодирование отсчетов сигнала на рис. 4.5 четырехразрядными целыми беззнаковыми числами в двоичной системе. В данном случае каждый уровень кодируется 4 – разрядным кодом с общим числом комбинаций M=2⁴=16. Согласно представлению в двоичной системе 0=0000, 1=0001, 2=0010, 3=0011, 4=0100, 5=0101, 6=0110, 7=0111, 8=1000, 9=1001, 10=1010, 11=1011 и т. д.

Таблица 4.1

n	0	1	2	3	4	5	6	7
xц(nT)	7	9	10	11	10	9	5	3
код	0111	1001	1010	1011	1010	1001	0101	0011

При представлении отсчетов сигнала в виде чисел с ограниченной разрядностью неизбежно происходит их округление. Разность между исходным и округленным значениями сигнала называется шумом квантования или погрешностью квантования.

Пусть квантованию подвергается гармонический сигнал с амплитудой А. Тогда число уровней квантования, укладывающихся в размахе сигнала определяется, как N=2А/Δ. В общем случае количество уровней квантования может быть определено выражением

,

где и – верхняя и нижняя границы диапазона изменения сигнала соответственно. Чем меньше Δ, тем меньше получаемая ошибка – шум квантования

,

где – результат квантования сигнала . Необходимое значение шага квантования обеспечивается выбором АЦП с требуемым числом разрядов.

При использовании системы с фиксированной запятой и представлении чисел в прямом коде шаг квантования равен:

,

где b - количество разрядов, определяющих модуль двоичного числа.

Если в результате квантования любое из значений сигнала x_a(t) округляется до значения, соответствующего значению ближайшего уровня квантования h_i, то возникающая при этом ошибка не превышает половины шага квантования т.е.

.

Если сигнал x_a(t) случайный и шаг квантования Δ достаточно мал по сравнения с диапазоном изменения сигнала, то считается, что ошибка квантования имеет равномерный закон распределения вероятности. Дисперсия шума квантования равна:

,

где - плотность вероятности. Математическое ожидание погрешности квантования составит . При const относительная погрешность квантования существенно зависит от текущего значения сигнала.

На практике шаг квантования выбирают исходя из уровня помех, присутствующих при измерении, передаче и обработке реальных сигналов. Отношение сигнал/шум:

,

где – дисперсия сигнала.

Аналого-цифровое преобразование сигнала предполагает его замену некоторыми квантованными значениями, а также образование кода уровня квантования. При этом образование кода происходит, как правило, одновременно с преобразованием измеряемой величины в квантованную. В настоящее время широкое распространение получили три метода аналого-цифрового преобразования сигнала: метод последовательного счета, метод последовательного приближения, метод считывания.

Метод последовательного счета. Данный метод использует последовательное во времени сравнение измеряемой величины x с известной квантованной величиной x_k, изменяющейся (возрастающей или убывающей) во времени скачком [31]. В данном случае считается, что измеряемая величина остается постоянной в течение времени измерения t_и. Каждый скачек величины x_k соответствует шагу квантования по уровню (рис. 4.6). В процессе сравнения образуется цифровой код, соответствующий номеру отождествляемого уровня квантования.

Рис. 4.6 Рис. 4.7

Метод последовательного приближения (сравнения и вычитания, поразрядного уравновешивания). Измеряемая величина последовательно сравнивается с известной квантованной величиной x_k [31]. Значение известной величины, при котором наступает равенство x_k=x, соответствует номеру отождествляемого уровня квантования (рис. 4.7).

Метод считывания. При этом методе происходит одновременное сравнение измеряемой величины x с известными значениями x_k1, x_k2, …, x_ki, … x_kN, значения которых равны уровням квантования [32]. Известная величина x_ki, равная измеряемой величине x, дает номер отождествляемого уровня квантования, в соответствии с которым образуется код (рис. 4.8).

Рис. 4.8