В развернутой форме записи система (2.2) имеет следующий вид:

x₁ = b₁₁x₁ + b₁₂x₂ + b₁₃x₃ + … + b_1nx_n + c₁

x₂ = b₂₁x₁ + b₂₂x₂ + b₂₃x₃ + … + b_2nx_n + c₂

. . . . . . . . . . . . . . . . .

x_n = b_n1x₁ + b_n2x₂ + b_n3x₃ + … + b_nnx_n + c_n

Вообще говоря, операция приведения системы к виду, удобному для итераций, не является простой и требует специальных знаний, а также существенного использования специфики системы.

Можно, например, преобразовать систему (2.1) следующим образом

x₁ = (b₁ - a₁₁ x₁ – a₁₂ x₂ - … - a_1n x_n) / a₁₁ + x₁,

x₂ = (b₂ - a₂₁ x₁ – a₂₂ x₂ - … - a_2n x_n) / a₂₂ + x₂,

…..

x_n = (b_n - a_n1 x₁ – a_n2 x₂ - … - a_nn x_n) / a_nn + x_n

если диагональные элементы матрицы А отличны от нуля. Можно преобразовать систему (2.1) в эквивалентную ей систему

x = (E-A)x+b.

Задав произвольным образом столбец начальных приближений х⁰ = (x₁⁰ , x₂⁰ , … , x_n⁰ )^T , подставим их в правые части системы (2.2) и вычислим новые приближения x¹ = (x₁¹ , x₂¹ , … , x_n¹ )^T , которые опять подставим в систему (2.2) и т.д. Таким образом, организуется итерационный процесс

x^k = Bx^k-1 + c , k = 1,2, …. ,. Известно, что система (2.1) имеет единственное решение х^* и последовательность {x^k} сходится к этому решению со скоростью геометрической прогрессии, если || B || < 1 в любой матричной норме. Т.е.

Т.е. для того, чтобы последовательность простых итераций сходилась к единственному решению достаточно, чтобы выполнялось одно из следующих условий:

1

j = 1

i

n

) max ( | b_ij | ) < 1 ;

n

n

2

i = 1 j=1

)   b_ij ² < 1;

n

3

ji

i = 1

) max ( | b_ij | ) < 1.

Метод Зейделя. Метод Зейделя является модификацией метода простых итераций. Суть его состоит в том, что при вычислении следующего : 2 в формуле x^k = Bx^k-1 + c , k = 1,2, …. используются вместо уже вычисленные ранее , т.е.

. (2.3) Такое усовершенствование позволяет ускорить сходимость итераций почти в два раза. Кроме того, данный метод может быть реализован на ЭВМ без привлечения дополнительного массива, т.к. полученное новое сразу засылается на место старого.

Схема алгоритма аналогична схеме метода простых итераций.

Самый простой способ приведения системы к виду, удобному для итераций, состоит в следующем. Из первого уравнения системы выразим неизвестное x₁:

x₁ = a₁₁^–1 (b₁ – a₁₂x₂ – a₁₃x₃ – … – a_1nx_n),

из второго уравнения – неизвестное x₂:

x₂ = a₂₁^–1 (b₂ – a₂₂x₂ – a₂₃x₃ – … – a_2nx_n),

и т. д. В результате получим систему

x₁ = b₁₂x₂ + b₁₃x₃ + … + b_1,n–1x_n–1 + b_1nx_n+ c₁ ,

x₂ = b₂₁x₁ + b₂₃x₃ + … + b_2,n–1x_n–1 + b_2nx_n+ c₂ ,

x₃ = b₃₁x₁ + b₃₂x₂ + … + b_3,n–1x_n–1 + b_3nx_n+ c₃ ,

. . . . . . . . . . . . . . . . . . . . . . .

x_n = b_n1x₁ + b_n2x₂ + b_n3x₃ + … + b_n,n–1x_n–1 + c_n ,

в которой на главной диагонали матрицы B находятся нулевые элементы. Остальные элементы выражаются по формулам

b_ij = –a_ij / a_ii, c_i = b_i / a_ii (i, j = 1, 2, …, n, j ≠ i) (2.4)

Конечно, для возможности выполнения указанного преобразования необходимо, чтобы диагональные элементы матрицы A были ненулевыми.

Введем нижнюю B₁ (получается из B заменой нулями элементов стоявших на главной диагонали и выше ее) и верхнюю B2 (получается из B заменой нулями элементов стоявших на главной диагонали и ниже ее) треугольные матрицы.

Заметим, что B = B₁ + B₂ и поэтому решение x исходной системы удовлетворяет равенству

x = B₁x + B₂ x + c (2.5)

Выберем начальное приближение x⁽⁰⁾ = [x₁⁽⁰⁾, x₂⁽⁰⁾, …, x_n⁽⁰⁾]^T. Подставляя его в правую часть равенства при верхней треугольной матрице B₂ и вычисляя полученное выражение, находим первое приближение

x⁽¹⁾ = B₁x⁽⁰⁾ + B₂x⁽¹⁾ (2.6)

Подставляя приближение x⁽¹⁾, получим

x⁽²⁾ = B₁x⁽¹⁾ + B₂x⁽²⁾ (2.7)

Продолжая этот процесс далее, получим последовательность x⁽⁰⁾, x⁽¹⁾, …, x⁽ⁿ⁾, … приближений к вычисляемых по формуле

x^(k+1) = B₁^(k+1) + B₂^(k) + c (2.8)

или в развернутой форме записи

x₁^(k+1) = b₁₂x₂^(k) + b₁₃x₂^(k) + … + b_1nx_n^(k) + c₁ ,

x₂^(k+1) = b₂₁x₁^(k+1) + b₂₃x₃^(k) + … + b_2nx_n^(k) + c₂ ,

x₃^(k+1) = b₃₁x₁^(k+1) + b₃₂x₂^(k+1) + … + b_3nx_n^(k) + c₃ ,

. . . . . . . . . . . . . . . . . . . . . . . . . .

x_n^(k+1) = b_n1x₁^(k+1) + b_n2x₂^(k+1) + b_n3x₃^(k+1) + … + c_n .

Объединив приведение системы к виду, удобному для итераций и метод Зейделя в одну формулу, получим

x_i^(k+1) = x_i^(k) – a_ii^–1(∑_j=1^i–1 a_ijx_j^(k+1) + ∑_j=1ⁿ a_ijx_i^(k) – b_i). (2.9)

Тогда достаточным условием сходимоти метода Зейделя будет условие доминированния диагональных элементов в строках или столбцах матрицы A, т.е.

a_ii>a_i1+ ……..+a_in для всех i=1,…n,

или a_jj>a_1j+…….+a_nj для всех j=1,….,n.

Методы простой итерации и Зейделя сходятся примерно так же, как геометрическая прогрессия со знаменателем || B || .

ЗАДАНИЕ. Методом простых итераций и методом Зейделя найти с точностью 0,0001 численное решение системы Ax=b,

где A = kC + D, A – исходная матрица для расчёта, k – номер варианта (0-15), матрицы С, D и вектор свободных членов b задаются ниже.

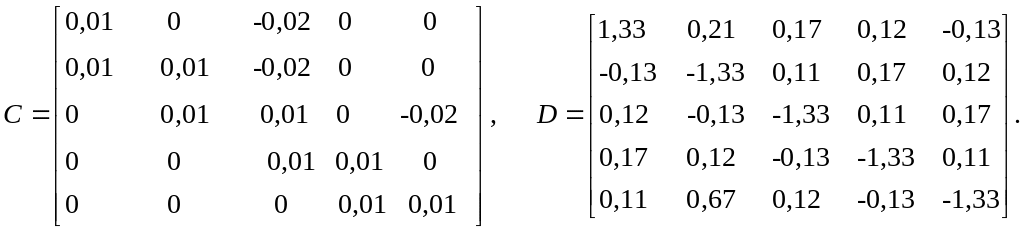
Вектор b= (1,2; 2,2; 4,0; 0,0; -1,2)^T.