12. Математические модели прикладных задач
12.1. Дифференциальное уравнение вынужденных колебаний
Движение материальной точки по прямой под действием силы притяжения к неподвижному центру, пропорциональной отклонению от него, и силы сопротивления среды, пропорциональной скорости движения точки, описывается дифференциальным уравнением
что следует из второго закона Ньютона. С учетом возбуждающей силы f(t) дифференциальное уравнение движения материальной точки принимает вид
При
отсутствии сопротивления среды (а=0) и
наличии периодической возбуждающей
силы
дифференциальное уравнение движения
принимает вид
Общее
решение однородного уравнения
характеризует собственные
колебания.
Частное решение неоднородного уравнения
при
характеризует вынужденные
колебания
материальной точки.
Общее решение неоднородного уравнения представляет собой наложение свободных и вынужденных колебаний (принцип суперпозиции сил), т.е.
Если
частота
внешней силы близка к частоте k
собственных колебаний, то амплитуда
очень велика, вследствие чего может
произойти разрушение всей колебательной
системы. Это явление носит название
резонанса.
В чисто
резонансном случае при
общее решение уравнения имеет вид
При
амплитуда вынужденных колебаний
неограниченно возрастает.
С учетом сопротивления среды и при синусоидальной вынуждающей силе дифференциальное уравнение движения принимает вид
Общее
решение однородного уравнения
при
и
описывает собственные колебания и при
стремится к нулю. Частное решение
неоднородного уравнения при больших t
описывает установившийся
режим и
соответствует вынужденным колебаниям.
Решение типовых примеров
Пример 1. Тело совершает 90 колебаний в минуту, амплитуда колебаний уменьшается вдвое в течение 15 с. Составить дифференциальное уравнение движения.
Решение. Так как тело совершает затухающие гармонические колебания, то закон движения имеет вид
где
- частота колебаний, а период колебаний
Из условия задачи следует, что одно
колебание тело совершает за 60/90 с.
Следовательно, Т=2/3 и
Учитывая, что при t=0
амплитуда колебания равна А, а при t=15
с
имеем
и
где А,
-произвольные
постоянные. Дифференциальное уравнение
второго порядка, общим решением которого
является x(t)
и корни характеристического уравнения
имеет вид
Пример
2. На идеально
гладкой плоскости, наклоненной к
горизонту под углом
(рис.12.1), находится груз массой m=1кг,
прикрепленный к пружине, жесткость
которой
Определить закон колебаний груза, если
он отпущен без начальной скорости из
положения, при котором пружина не
деформирована.
Р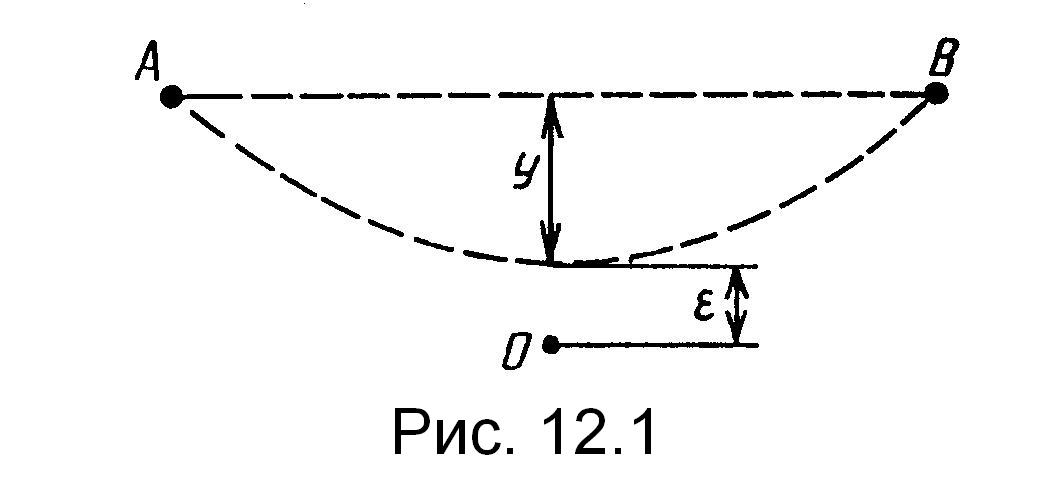
ешение.
На рис. 12.1 ось Ох совпадает с направлением
движения груза вдоль наклонной плоскости,
за начало координат выбрана точка
статического равновесия. Сила упругости
пружины
где
-изменение
длины пружины по сравнению с ее
естественным (ненапряженным) состоянием:
l-удлинение
пружины при равновесии. Обозначим через
длину пружины до деформации. Так как на
систему, кроме силы упругости, действует
еще вес груза
где
то дифференциальное уравнение движения
В
точке х=0 имеет место равновесие, то есть
при этом
Из предыдущего уравнения имеем
следовательно,
т.е. дифференциальное уравнение закона
движения груза не зависит от статического
удлинения пружины. Учитывая, что в
начальный момент времени t=0
пружина была не деформирована и груз
был отпущен без начальной скорости,
математическую модель движения груза
запишем в виде
где
или
Используя
данные задачи, имеем
Следовательно, амплитуда колебаний
А=0,1см, а период колебаний
