Краткая теоретическая часть:

Предполагается, что функция задана в виде таблицы конечного числа точек:

х	х0	х1	…	хn	,
у	y0	y1	…	yn

например, получена экспериментально или по известной (достаточно сложной) формуле для . Здесь х_i и y_i (i=0,1,…, n) – произвольные числа и при этом все х_i различны и упорядочены: 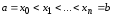. При этом множество всех узлов х_i называют сеткой, если узлы являются равноотстоящими, т.е. х_i= х₀+ih, где .

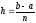Используя исходные данные, затем подбирают функцию 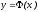несложного вида, значения которой при 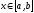являются приближенными для .

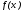Важным здесь следует отметить не только то, чтобы 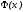имела простой вид и хорошо приближала 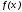, но и чтобы ее практически можно было найти. В этом смысле наиболее подходящий вид для 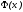- многочлен 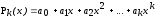. Но и в этом случае не все просто с вычислительной стороны. Как правило, при нахождении значений нельзя обойтись без многочисленных промежуточных округлений числе, что часто приводит к большой потере точности коэффициентов 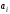. И может случиться так, что полученный в результате многочлен будет гораздо хуже приближать данную функцию 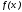, чем истинный многочлен 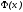, а это недопустимо.

При расчетах чаще всего нельзя заранее предсказать оптимальный режим вычислений, т.е. указать минимальную разрядность счета (начав с какой-либо) до тех пор, пока, не добьются удовлетворительных результатов, т.е. совпадения цифр в требуемых разрядах результата.

Определение 1. Функция называется интерполяционной для 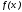, если выполнены условия: 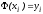, i=0,1, …, n, т.е график 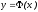проходит через все заданные точки .

Известно, что для данной таблицы всегда существует и притом единственны интерполяционный многочлен (ИМ) степени n. Будем обозначать ИМ через 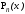. Для него верно:

,

i=0,1, …, n.

(1)

Остаточный член для , т.е. величина , имеет вид:

(2)

где П_n+1(x)=(x-x₀)(x-x₁)…(x-x_n).

Так как точка ξ практически всегда неизвестна, то при оценке погрешности для 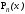пользуются неравенством:

.

(2´)

А) ИМ Лагранжа имеет вид:

,

(3)

где .

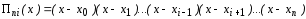В) ИМ Ньютона

ИМ Ньютона строятся на сетке и выражаются через конечные разности.

Определение 2. Величина 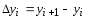называется конечной разностью первого порядка функции 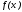в точке 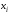с шагом h. По аналогии имеем: 2-ая конечная разность – это , …,

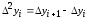k-ая конечная разность – это .

Конечные разности удобно записывать в виде таблицы 1 (в каждом столбце, кроме столбца , из последующего числа вычитается предыдущее число и разность записывается в следующем столбце).

Но если 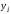является приближенным (например, из-за округлений), то в этой связи с ростом порядка конечных разностей погрешность растет (удваивается на каждом шаге). Поэтому исходные данные 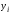надо брать с повышенной точностью.

Таблица 1

xi	yi	Δ yi	Δ^2 yi	Δ^3 yi	Δ^4 yi	…
x0	y0	Δ y0	Δ^2 y0	Δ^3 y0	Δ^4 y0	…
x1	y1	Δ y1	Δ^2 y1	Δ^3 y1	…
x2	y2	Δ y2	Δ^2 y2	…
x3	y3	Δ y3	…
x4	y4	…
…	…

1-ый ИМ Ньютона имеет вид:

.

(4

ИМ Ньютона играет в численном анализе роль, аналогичную роли формулы Тейлора в математическом анализе. Так при использовании формулы (4), если слагаемые, начиная с какого-то номера становятся малыми, то ими пренебрегают.

Если ввести обозначение: t=(x-x₀)/h, то 1-ый ИМ Ньютона примет вид:

(5)

0 ≤ t ≤ n; t=(x-x₀)/h

Оценка погрешности:

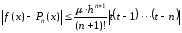; 0 ≤ t ≤ n; x є [x₀;x_n], μ=max│f⁽ⁿ⁺¹⁾(x)│

Если ввести обозначение: t=(x-x_n)/h, то получим 2-ый ИМ Ньютона:

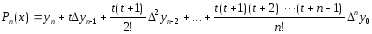(6)

─ n ≤ t ≤ 0; t=(x-x_n)/h

Оценка погрешности:

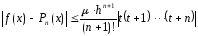; -n ≤ t ≤ 0; x є [x₀;x_n], μ=max│f⁽ⁿ⁺¹⁾(x)│

Решение:
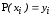
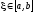
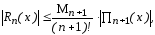