Полином Ньютона.

i	0	1	2	3	4	5
x	0,5	0,7	0,9	1,1	1,3	1,5
y	3,150	3,171	3,181	3,179	3,165	3,140

Рассчитаем конечные разности:

∆у₀=у₁-у₀ ∆²у₀=∆у₁-∆у₀ ∆³у₀=∆²у₁-∆²у₀ ∆⁴у₀=∆³у₁-∆³у₀ ∆⁵у₀=∆⁴у₁-∆⁴у₀

∆у₁=у₂-у₁ ∆²у₁=∆у₂-∆у₁ ∆³у₁=∆²у₂-∆²у₁ ∆⁴у₁=∆³у₂-∆³у₁

∆у₂=у₃-у₂ ∆²у₂=∆у₃-∆у₂ ∆³у₂=∆²у₃-∆²у₂

∆у₃=у₄-у₃ ∆²у₃=∆у₄-∆у₃

∆у₄=у₅-у₄

Полученные данные сведем в таблицу:

	у	∆у	∆^2у	∆^3у	∆^4у	∆^5у
0	3,150	0,021	-0,011	-0,001	0,001	0
1	3,171	0,010	-0,012	0	0,001
2	3,181	-0,002	-0,012	0,001
3	3,179	-0,014	-0,011
4	3,165	-0,025
5	3,140

Интерполяционная формула Ньютона:

P₅(x)=

По условию задачи h=0,2.

P₅(x)=

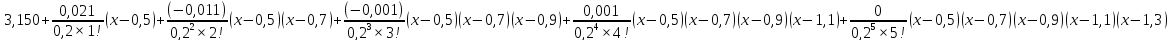
P₅(x)=3,150+0,105(х-0,5)+(-0,1375)(х²-1,2х+0,35)+(-0,021)(х³-2,1х²+1,43х-0,315)+0,026(х⁴-3,2х³+3,74х²-1,89х+0,35)+0

P₅(x)=3,150+0,105х-0,0525+(-0,1375х²)+0,165х-0,048+(-0,021х³)+0,044х²-0,03х+0,007+0,026х⁴-0,0832х³+0,097х²-0,049х+0,009

P₅(x)=0,026х⁴-0,104х³+0,003х²+0,191х+3,066

Построим получившийся график.

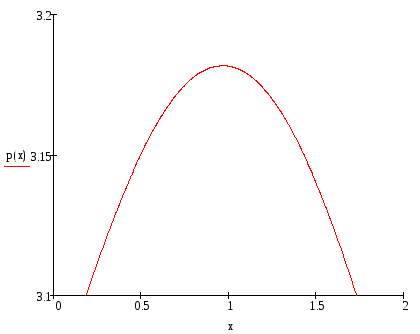
Произведем проверку:

P₅(1)=0,026*0,7⁴-0,104*0,7³+0,003*0,7²+0,191*0,7+3,066=3,171

P₅(2)=0,026*0,9⁴-0,104*0,9³+0,003*0,9²+0,191*0,9+3,066=3,181

P₅(3)=0,026*1,1⁴-0,104*1,1³+0,003*1,1²+0,191*1,1+3,066=3,179

P₅(4)=0,026*1,3⁴-0,104*1,3³+0,003*1,3²+0,191*1,3+3,066=3,165

P₅(5)=0,026*1,5⁴-0,104*1,5³+0,003*1,5²+0,191*1,5+3,066=3,140

После проведенной проверки найдем F(х^**)

F(1.35)=3.16

Полином Лагранжа.

P₅(x)=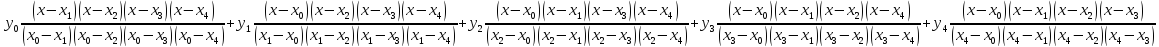

P₅(x)=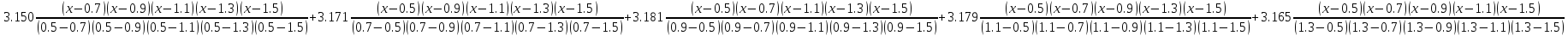

Р(х)=0,13020833333333334*х⁴-0,500000000000000024*х³+0,5494791666666666698*х²-0,13000000000000001452*х+3,131992187500000000

Проверим полином по табличным координатам:

Р(0,5)=3,150 ; Р(0,7)=3,171; Р(0,9)=3,181; Р(1,1)=3,179; Р(1,3)=3,165.

по полученному полиному вычисляем Р(х^*):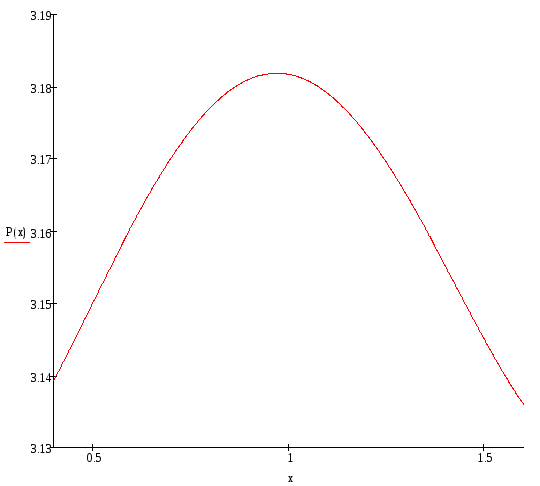

Р(х^*)→Р(0,55)=3,155

Проведем оценку погрешности:

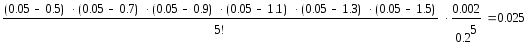
ЗАДАЧА № 3

Найти наименьший положительный корень уравнения комбинированным методом с точностью до 0,0001. Уравнение: 3 – x – lg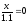

Краткая теоретическая часть:

Методы хорд и касательных дают приближения корня с разных сторон. Поэтому их часто применяют в сочетании друг с другом, и уточнение корня происходит быстрее.

Пусть дано уравнение f(x)=0, корень ξ отделён и находится на отрезке [a,b].

Если f (x)·f ″(x) < 0, то методом хорд получаем значение корня с избытком, а методом касательных – с недостатком.

Если f (x)·f ″(x) > 0, то метод хорд даёт приближение корня с недостатком, а метод касательных – с избытком.

Рассмотрим случай, когда f (b) < 0, f ″(x) > 0 (рис.1), то со стороны конца а лежат приближённые значения корня, полученные по методу касательных, а со стороны конца b – значения, полученные по методу хорд.

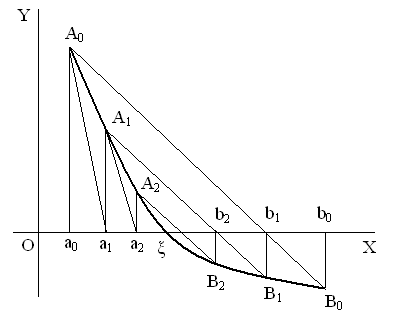
Рис.1 Иллюстрация комбинированного метода.

Тогда , .

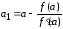Теперь истинный корень ξ находится на интервале [a₁,b₁]. Применяя к этому интервалу комбинированный метод, получаем:

,

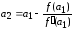и вообще

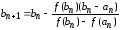, . (1)

Для случая, когда f (b)·f ″(x) > 0, то рассуждая аналогично, получим следующие формулы для уточнения корня уравнения:

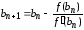, . (2)

Комбинированный метод очень удобен при оценке погрешности вычислений. Процесс вычислений прекращается, как только станет выполняться неравенство

‌‌‌‌‌‌‌ |b_n+1–a_n+1| < ε.

Корень уравнения есть среднее арифметическое последних полученных значений: ξ=(‌a_n+1+b_n+1)/2

Решение:

Сначала найдем точное решение в Mathcad

х=2,622652

Построим графики Функции и 2х ее производных

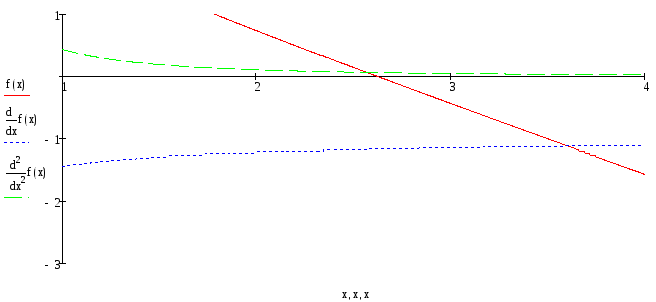
Далее для приближенного вычисления применим метод хорд и касательных

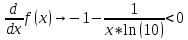
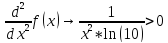
Возьмем отрезок равный единице в месте пересечения только нашей функции с осью Х

Определим где касательная, а где хорда

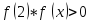
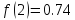- Касательная

– Хорда

Подставим данные в таблицу Excel:

i	Xx	Zx	F(x)	F(z)	dF(x)	E
0	2	3	0,74036269	-0,43572857	-2,1512925	1
1	2,3441478	2,6295113	0,3272598	-0,0079936	-1,9822696	0,2853634
2	2,5092414	2,6227072	0,1326089	-0,0000643	-1,9176419	0,1134658
3	2,5783934	2,6226522	0,0516501	-0,0000002	-1,8930309	0,0442588
4	2,6056777	2,6226520	0,0197942	0,0000000	-1,8836799	0,0169743
5	2,6161860	2,6226520	0,0075380	0,0000000	-1,8801305	0,0064660
6	2,6201953	2,6226520	0,0028637	0,0000000	-1,8787838	0,0024567
7	2,6217196	2,6226520	0,0010869	0,0000000	-1,8782728	0,0009325
8	2,6222982	2,6226520	0,0004124	0,0000000	-1,8780790	0,0003538
9	2,6225178	2,6226520	0,0001564	0,0000000	-1,8780055	0,0001342
10	2,6226011	2,6226520	0,0000593	0,0000000	-1,8779776	0,0000509
11	2,6226327	2,6226520	0,0000225	0,0000000	-1,8779670	0,0000193
12	2,6226447	2,6226520	0,0000085	0,0000000	-1,8779630	0,0000073
Корень	2,62264835179927

ЗАДАЧА № 4

Найти численное решение задачи Коши для данного дифференциального

уравнения и начального условия 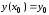на отрезке 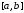с шагом 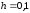методом Эйлера.

Дифференциальное уравнение:

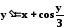
Начальное условие:

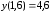
Отрезок: [1.6; 2.6]