Краткая теоретическая часть

Метод Рунге-Кутты используют для расчета стандартных моделей достаточно часто, так как при небольшом объеме вычислений он обладает точностью метода Ο⁴(h).

Для построения разностной схемы интегрирования воспользуемся разложением функции

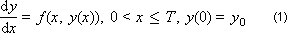
в ряд Тейлора:

Заменим вторую производную в этом разложении выражением

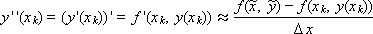
где

Причем Δx подбирается из условия достижения наибольшей точности записанного выражения. Для дальнейших выкладок произведем замену величины «y с тильдой» разложением в ряд Тейлора:

Для исходного уравнения (1) построим вычислительную схему:

которую преобразуем к виду:

Введем следующие обозначения:

Эти обозначения позволяют записать предыдущее выражение в форме:

Очевидно, что все введенные коэффициенты зависят от величины Δx и могут быть определены через коэффициент α, который в этом случае играет роль параметра:

Окончательно схема Рунге-Кутты принимает вид:

Та же схема в форме разностного аналога уравнения (1):

При α = 0 получаем как частный случай уже известную схему Эйлера:

При α = 1:

При α = 1 проведение расчетов на очередном шаге интегрирования можно рассматривать как последовательность нижеследующих операций.

1. Вычисляется выражение, представляющее собой полушаг интегрирования по схеме Эйлера, то есть определяется приближенное значение искомой функции в точке x_k + h/2:

2. Для той же промежуточной точки находится приближенное значение производной:

3. Определяется уточненное значение функции в конечной точке всего шага, причем по схеме Эйлера с вычисленным на предыдущем шаге значением производной:

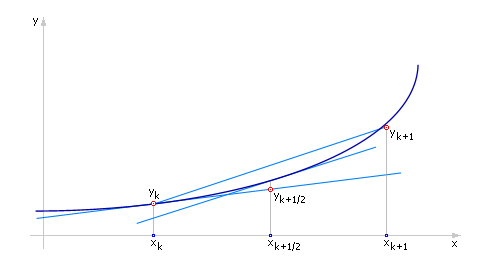
Геометрические построения (см. рис. 15.1) показывают, что получаемое в такой последовательности решение лежит «ближе» к истинному, чем вычисляемое по схеме Эйлера, то есть следует ожидать более высокой точности решения, получаемого методом Рунге-Кутты. Ранее мы назвали эту схему «модифицированным методом Эйлера».

Рис. 1.1. Иллюстрация расчета на шаге методом Рунге-Кутты при значении параметра α = 1

Теперь рассмотрим схему при α = 0.5 (геометрическая интерпретация результата приведена на рис. 1.2).

1. Выполняется полный шаг метода Эйлера с целью определения приближенного значения искомой функции на конце отрезка интегрирования:

2. Для этой же точки вычисляется приближенное значение производной:

3. Находится среднее значение двух производных, определенных на концах отрезка:

4. Вычисляется значение искомой функции в конечной точке всего шага по схеме Эйлера с усредненным значением производной:

Рис. 1.2. Иллюстрация расчета на шаге методом Рунге-Кутты при значении параметра α = 0.5

Иногда получающееся выражение называют схемой (методом) Эйлера-Коши. Геометрически понятно, что получаемый указанным способом результат также должен быть «ближе» к истинному решению, чем получаемый по схеме Эйлера.

Решение

Дифференциальное уравнение:

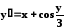
Начальное условие:

Отрезок: [1.6; 2.6]

Шаг:

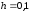
Шаг 1

x₀=1.6; y₀=4.6;

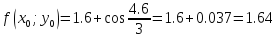
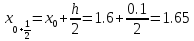
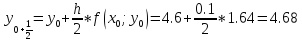
x₁= x₀₊h=1.6+0.1=1.7;

Шаг 2

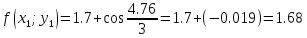
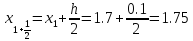
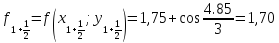
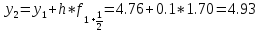
Шаг 3

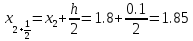
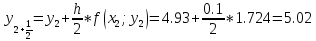
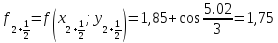
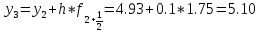
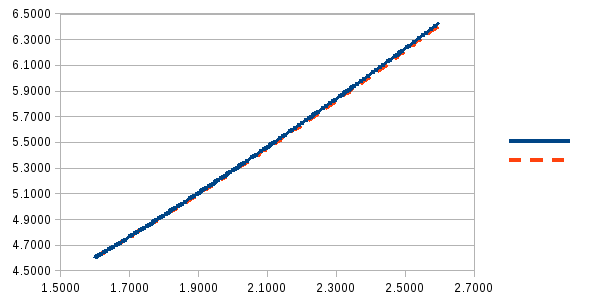
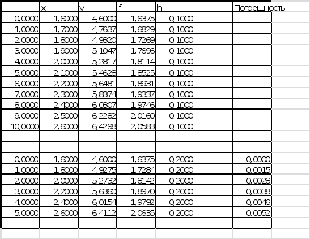
Расчет производим, таким образом, до значения Х₁₀=2,6 с помощью Excel.

В первой части таблицы приведены расчеты с шагом 0,1, а во второй части с шагом 0,05, а также погрешность двойного расчета.

Построим график по вычисленным расчетам: