
Задачи Матюнин / ЗАДАНИЕ 2
.docМинистерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
Пермский национальный исследовательский политехнический университет
Факультет Аэрокосмический
Специальность 24.05.02 Проектирование авиационных
и ракетных двигателей
Специализация Проектирование авиационных двигателей
и энергетических установок
Кафедра Авиационные двигатели
Дисциплина «Уравнения математической физики»
Отчёт о решении задачи №2
|
На тему |
Градиент от скалярного произведения |
|
двух векторов |
|
|
Студенты |
Гамов Антон Сергеевич |
( |
|
) |
|
|
Петров Кирилл Олегович |
( |
|
) |
|
|
Похлебаев Георгий Юрьевич |
( |
|
) |
|
Группа |
АД-16-2с |
|
|
|
Принял
|
|
( |
доц. каф. АД Матюнин В.П. |
) |
|
Дата: |
|
|
|
Пермь 2018 г.
ЗАДАНИЕ
Вывести формулу для нахождения градиента скалярного произведения двух векторов.
ВВЕДЕНИЕ
Определимся с понятиями скалярное произведение и градиент. Скалярным произведением двух векторов A и B называется число, равное произведению длин этих векторов на косинус угла между ними:
![]() (1)
(1)
Или, выражая в проекциях на оси, получим:
![]() (2)
(2)
Градиент - вектор, указывающий направление наибольшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой, а по величине равный скорости роста этой величины в этом направлении. Математически выражается следующей записью:
![]() (3)
(3)
Целью дальнейшей работы станет объединений двух этих понятий в единую формулу.
ФИЗИЧЕСКАЯ МОДЕЛЬ
Скалярное произведение двух векторов часто используется в физике для вычисления какой-либо величины. Поэтому построим модель на основе вычисления механической работы, которая в общем случае равна произведению вектора силы на вектор перемещения:
![]() (4)
(4)
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
Рассмотренную физическую модель можно применить для создания математической модели. Следует учесть, что работа не является векторной величиной, поэтому не имеет направления. Она лишь может оцениваться как полезная, отрицательная и нулевая. Но градиент этой величины всегда будет указывать наибольшую скорость возрастания функции. То есть задача сводится в частном случае, рассматриваемом в данном задании, к вычислению grad(R*S).
РЕШЕНИЕ
Решение данной задачи рассмотрим на конкретном примере: градиент механической работы. Работа находится как скалярное произведение векторов силы и перемещения:
![]() , ()
, ()
где R=Rxi+ Ryj+ Rzk, S=Sxi+ Syj+ Szk.
Тогда градиент от их произведения будет иметь вид:
![]() ()
()
Для уменьшения объёма записей произведём вычисления по орту i:
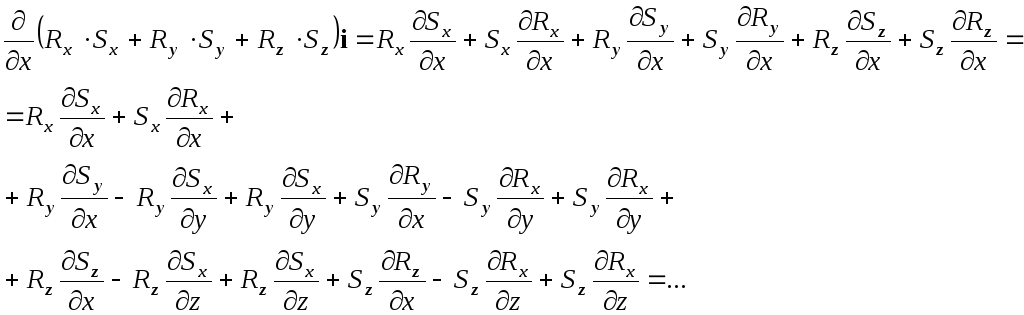
Заметим, что при группировке слагаемых выявляются части ротора, поэтому производим следующие действия:
![]()
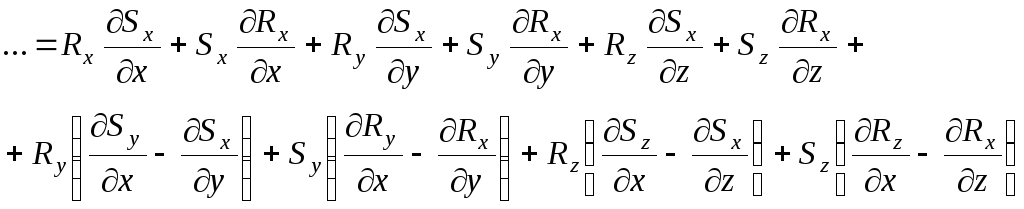
Выделенные в
скобки части являются угловыми скоростями
вращения, так
![]() есть угловая скорость вращения вектора
S вокруг оси, то
есть
есть угловая скорость вращения вектора
S вокруг оси, то
есть
![]() .
Аналогично с остальными скобками.
.
Аналогично с остальными скобками.
В итоге получаем:
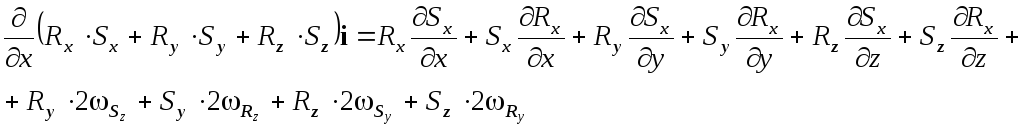
Аналогично получаем для ортов j и k:
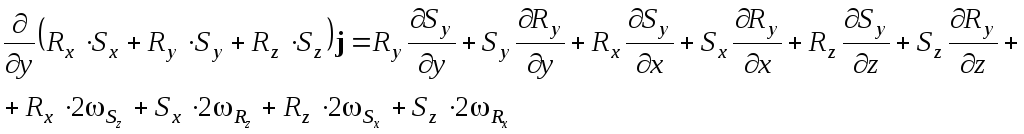
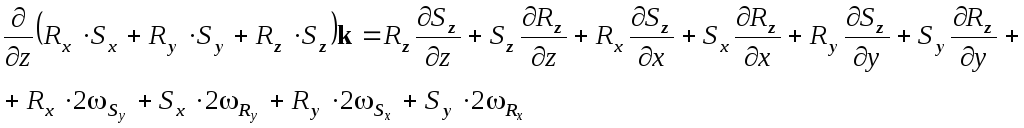
Объединяя три компонента, имеем выражение:
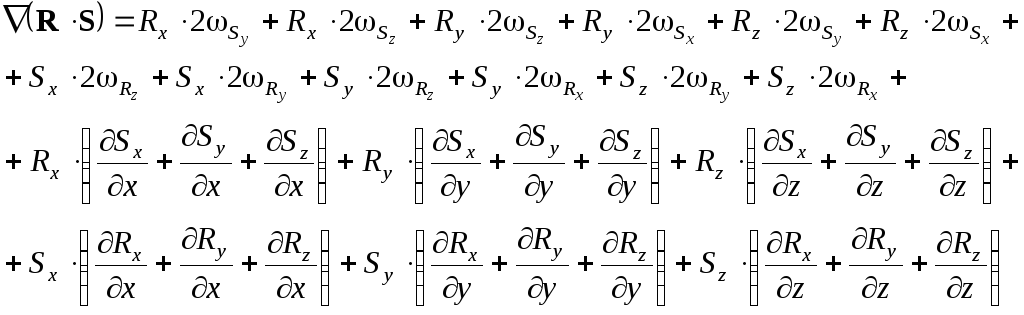
Учитывая, что
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
получаем окончательное выражение:
,
получаем окончательное выражение:
![]()
ОЦЕНКА ДОСТОВЕРНОСТИ И АНАЛИЗ РЕЗУЛЬТАТОВ
ВЫВОДЫ
