Теория вероятностей вычисляет вероятности различных событий. Основным в теории вероятностей является понятие случайного события.

Например, вы бросаете монету, она случайным образом падает на герб или решку. Заранее вы не знаете, на какую сторону монета упадет. Вы заключаете договор страхования, заранее вы не знаете, будут или нет проводиться выплаты.

В актуарных расчетах нужно уметь оценивать вероятность различных событий, поэтому теория вероятностей играет ключевую роль. Ни одна другая область математики не может оперировать с вероятностями событий.

Рассмотрим более подробно подбрасывание монеты. Имеется 2 взаимно исключающих исхода: выпадение герба или выпадение решки. Исход бросания является случайным, так как наблюдатель не может проанализировать и учесть все факторы, которые влияют на результат. Какова вероятность выпадения герба? Большинство ответит ½, но почему?

Пусть формально А обозначает выпадение герба. Пусть монета бросается n раз. Тогда вероятность события А можно определить как долю тех бросков, в результате которых выпадает герб:

                  (1)

где n общее количество бросков, n(A) число выпадений герба.

Отношение (1) называется частотой события А в длинной серии испытаний.

Оказывается, в различных сериях испытаний соответствующая частота при больших n группируется около некоторой постоянной величины Р(А). Эта величина называется вероятностью события А и обозначается буквой Р – сокращение от английского слова probability – вероятность.

Формально имеем:

       (2)

Этот закон называется законом больших чисел.

Если монета правильная (симметричная), то вероятность выпадения герба равняется вероятности выпадения решки и равняется ½.

Пусть А и В некоторые события, например, произошел или нет страховой случай. Объединением двух событий называется событие, состоящее в выполнении события А, события В, или обоих событий вместе. Пересечением двух событий А и В называется событие, состоящее в осуществлении как события А, так и события В.

Основные правила исчисления вероятностей событий являются следующие:

1. Вероятность любого события заключена между нулем и единицей:

2. Пусть а и в два события, тогда:

 

           (3)

Читается так: вероятность объединения двух событий равна сумме вероятностей этих событий минус вероятность пересечения событий. Если события являются несовместными или непересекающимися, то вероятность объединения (суммы) двух событий равна сумме вероятностей. Этот закон называется законом сложения вероятностей.

Мы говорим, что события является достоверным, если его вероятность равна 1. При анализе тех или иных явлений возникает вопрос, как влияет наступление события В на наступление события А. Для этого вводится условная вероятность:

         (4)

 

Читается так: вероятность наступления А при условии В равняется вероятности пересечения А и В, деленной на вероятность события В. В формуле (4) предполагается, что вероятность события В больше нуля.

Формулу (4) можно записать также в виде:

       (5)

Это формула умножения вероятностей.

Условную вероятность  называют также апостериорной вероятностью события А – вероятность наступления А после наступления В. В этом случае саму вероятность  называют априорной вероятностью. Имеется еще несколько важных формул, которые интенсивно используются в актуарных расчетах.

Формула полной вероятности

Допустим, что проводится опыт, об условиях которого можно заранее сделать взаимно исключающие друг друга предположения (гипотезы):

Мы предполагаем, что имеет место либо гипотеза , либо … либо . Вероятности этих гипотез известны и равны:

Тогда имеет место формула полной вероятности:

        (6)

Вероятность наступления события А равна сумме произведений вероятности наступления А при каждой гипотезе на вероятность этой гипотезы.

Формула Байеса

Она позволяет пересчитывать вероятность гипотез в свете новой информации, которую дал результат А. Формула Байеса в известном смысле является обратной к формуле полной вероятности.

     (7)

 

Рассмотрим следующую практическую задачу.

Задача 1. Предположим, произошла авиакатастрофа и эксперты заняты исследованием ее причин. Заранее известны 4 причины, по которым произошла катастрофа: либо причина , либо , либо , либо . По имеющейся статистике эти причины имеют следующие вероятности:  

При осмотре места катастрофы найдены следы воспламенения горючего, согласно статистике вероятность этого события при тех или иных причинах такая:

 

Вопрос: какая причина катастрофы наиболее вероятна?

Вычислим вероятности причин при условия наступления события А.

 

Отсюда видно, что наиболее вероятной является первая причина, так как ее вероятность максимальна.

Задача 2. Рассмотрим посадку самолета на аэродром.

При посадке погодные условия могут быть такими: низкой облачности нет ( ), низкая облачность есть ( ). В первом случае вероятность благополучной посадки равна P1. Во втором случае – Р2. Ясно, что P1>P2.

Приборы, обеспечивающие слепую посадку, имеют вероятность безотказной работы Р. Если есть низкая облачность и приборы слепой посадки отказали, вероятность удачного приземления равна Р3, причем Р3<Р2. Известно, что для данного аэродрома доля дней в году с низкой облачностью равна .

Найти вероятность благополучной посадки самолета.

Имеем:

 

 

Нужно найти вероятность .

Имеются два взаимно исключающих варианта: приборы слепой посадки действуют, приборы слепой посадки отказали, поэтому имеем:

Отсюда по формуле полной вероятности:

Задача 3. Страховая компания занимается страхованием жизни. 10% застрахованных в этой компании являются курильщиками. Если застрахованный не курит, вероятность его смерти на протяжении года равна 0.01 Если же он курильщик, то эта вероятность равна 0.05.

Какова доля курильщиков среди тех застрахованных, которые умерли в течение года?

Варианты ответов: (А) 5%, (Б) 20%, (В) 36 %, (Г) 56%, (Д) 90%.

Решение

Введём события:

1.  = {застрахованный – курильщик}

2.  = {застрахованный – не курильщик}

3.  = {застрахованный умер в течение года}

 

Условие задачи означает, что

Кроме того, поскольку события  и  образуют полную группу попарно несовместимых событий, то . Интересующая нас вероятность – это .

Используя формулу Байеса, мы имеем:

,

поэтому верным является вариант (В).

Задача 4. Страховая компания продаёт договора страхования жизни трёх категорий: стандартные, привилегированные и ультрапривилегированные. 50% всех застрахованных являются стандартными, 40% - привилегированными и 10% - ультрапривилегированными. Вероятность смерти в течение года для стандартного застрахованного равна 0.010, для привилегированного – 0.005, а для ультра привилегированного – 0.001.

Чему равна вероятность того, что умерший застрахованный является ультрапривилегированным?

Решение

Введем в рассмотрение следующие события:

1.  = {застрахованный является стандартным}

2.  = {застрахованный является привилегированным}

3.  = {застрахованный является ультрапривилегированным}

4.  = {застрахованный умер в течение года}

В терминах этих событий интересующая нас вероятность – это . По условию:

Поскольку события , ,  образуют полную группу попарно несовместимых событий, используя формулу Байеса мы имеем:

 

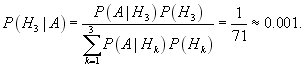
Случайные величины и их характеристики

Пусть  некоторая случайная величина, например, ущерб от пожара или величина страховых выплат. Случайная величина полностью характеризуется своей функцией распределения.

Определение. Функция  называется функцией распределения случайной величины ξ. Определение. Если существует такая функция , что для произвольных a<b выполнено

,

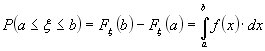то говорят, что случайная величина ξ имеет плотность распределения вероятности f(x).

Определение. Пусть . Для непрерывной функции распределения F теоретической α-квантилью  называется решение уравнения . Такое решение может быть не единственным.

Квантиль уровня ½ называется теоретической медианой, квантили уровней ¼ и ¾ - нижней и верхней квартилями соответственно.

В актуарных приложениях важную роль играет неравенство Чебышева:

при любом

 - символ математического ожидания. Читается так: вероятность того, что модуль  больше  меньше или равняется математическому ожиданию величины модуль , деленному на .

 

Время жизни как случайная величина

Неопределенность момента смерти является основным фактором риска при страховании жизни.

Относительно момента смерти отдельного человека нельзя сказать ничего определенного. Однако если мы имеем дело с большой однородной группой людей и не интересуемся судьбой отдельных людей из этой группы, то мы находимся в рамках теории вероятностей как науки о массовых случайных явлениях, обладающих свойством устойчивости частот.

Соответственно, мы можем говорить о продолжительности жизни как о случайной величине Т.

 

Функция выживания

В теории вероятностей описывают стохастическую природу любой случайной величины Т функцией распределения F (x), которая определяется как вероятность того, что случайная величина Т меньше, чем число x:

.

В  актуарной математике приятно работать не с функцией распределения, а с дополнительной функцией распределения . Применительно к продолжительной жизни  – это вероятность того, что человек доживет до возраста x лет. Функция

называется функцией выживания (survival function):

Функция выживания обладает следующими свойствами: