- •Глава 1. Элементы теории функции комплексного переменного
- •Комплексные числа и действия над ними
- •Упражнения
- •Упражнения для самостоятельной работы
- •2. Множества точек, линии, области на комплексной плоскости
- •Упражнения
- •Упражнения для самостоятельной работы
- •3. Функции комплексного переменного. Предел. Непрерывность функции. Основные элементарные функции
- •1. Дробно - рациональная функция
- •Упражнения для самостоятельной работы
- •4. Производная функции комплексного переменного. Условия дифференцируемости. Аналитические функции. Понятие о конформном отображении
- •Упражнения
- •Упражнения для самостоятельной работы
- •5. Интегрирование функции комплексного переменного
- •5.1. Интеграл от функции комплексного переменного
- •5.2. Вычисление интеграла от аналитической функции
- •5.3. Интегральная формула Коши
- •Упражнения
- •Упражнения для самостоятельной работы
- •6. Ряды в комплексной области
- •6.1. Ряды с комплексными членами Ряд
- •6.2. Ряды Тейлора и Лорана
- •Упражнения
- •Упражнения для самостоятельной работы
- •7. Изолированные особые точки функции комплексного переменного
- •7.1. Классификация изолированных особых точек
- •7.2. Ряды и особые точки
- •7.3. Нули аналитической функции. Связь между нулем и полюсом
- •7.4. Особенности функции в бесконечно удаленной точке
- •Точка называется существенно особой для функции, еслине существует.
- •Упражнения
- •Упражнения для самостоятельной работы
- •8. Вычеты и их применение к вычислению контурных интегралов
- •8.1. Вычет функции и его вычисление
- •8.2. Теоремы о вычетах и их применение к вычислению контурных интегралов
- •Упражнения
- •Упражнения для самостоятельной работы
- •8.3. Применение вычетов к вычислению определенных и несобственных интегралов
- •Упражнения для самостоятельной работы
- •Упражнения для самостоятельной работы
Упражнения
Решить уравнение
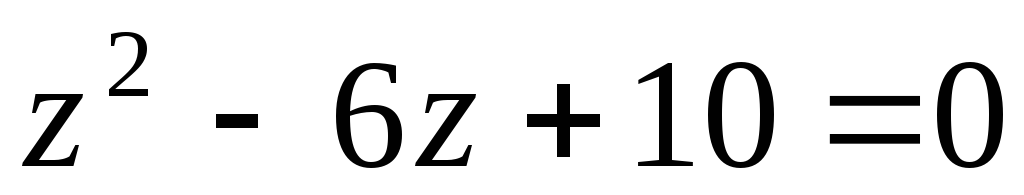 .
.
Решение.
1-й способ:
![]() .
.
![]() ,
,![]() ,
,![]() .
.
2-й
способ: В
результате подстановки
![]() в данное уравнение имеем
в данное уравнение имеем![]() ,
откуда после преобразований получим
систему уравнений
,
откуда после преобразований получим
систему уравнений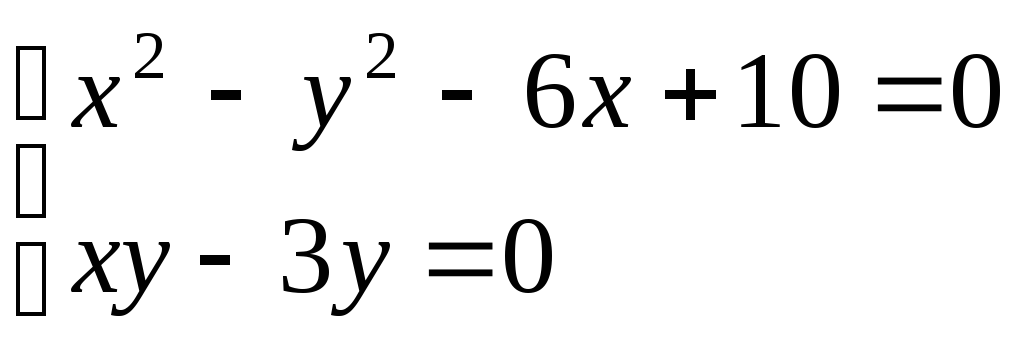 .
Решая систему, получим
.
Решая систему, получим![]() ,
,![]() .
.
Найти
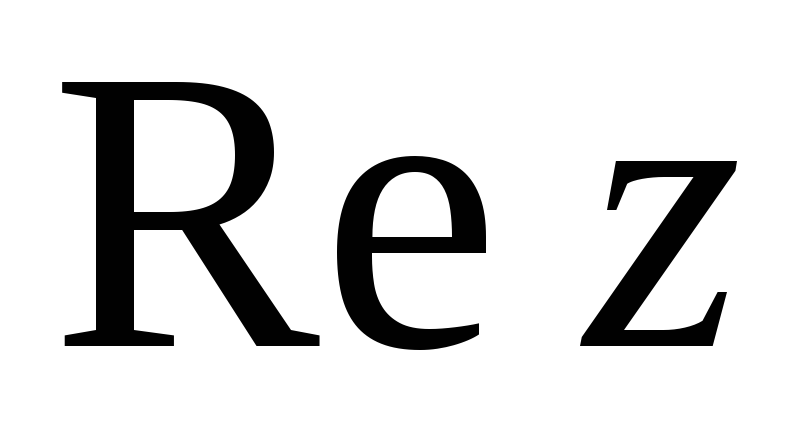 и
и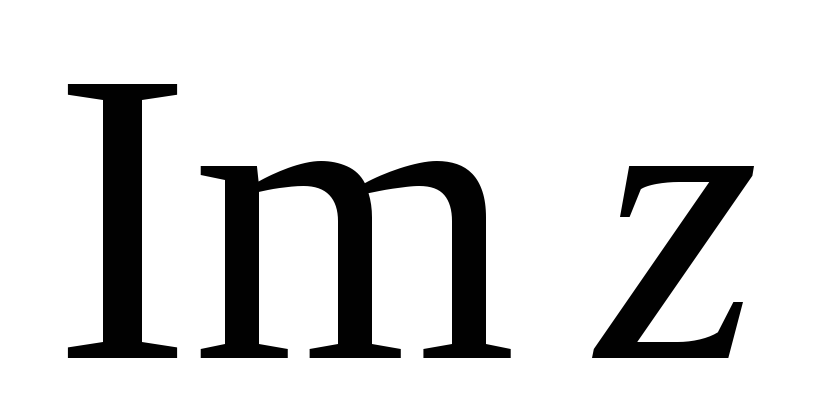 ,
если
,
если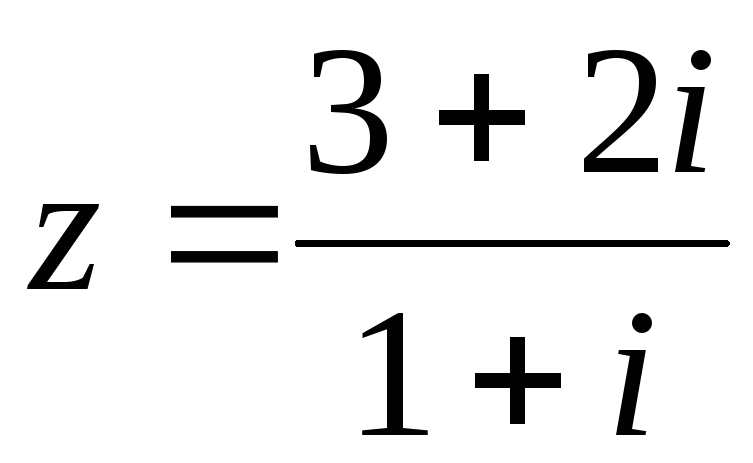 .
.
Решение:
![]() ,
откуда
,
откуда![]() ,
,![]() .
.
Выяснить геометрический смысл модуля разности
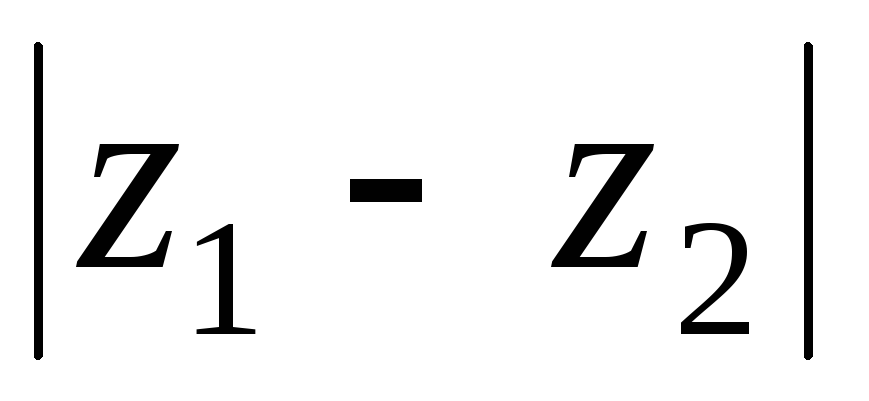 двух комплексных чисел
двух комплексных чисел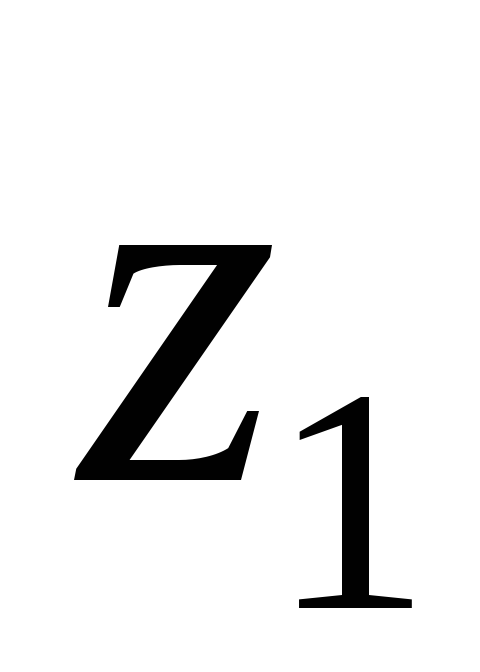 и
и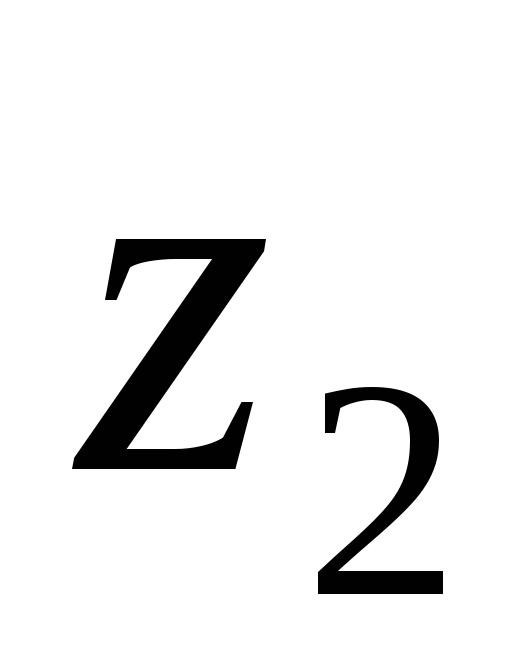 .
.
Решение:
![]() .
.
Следовательно,
![]() есть расстояние между точками
есть расстояние между точками![]() ,
и
,
и![]() (рис. 1.2).
(рис. 1.2).
|
Рис.1.2 |
Если
изобразить комплексное число с помощью
вектора, то действительная и мнимая
части вектора
|
сводится к вычитанию векторов, изображающих эти числа.
Как
видно из рис. 1.2,
![]() есть длина вектора
есть длина вектора![]() ,
т.е. расстояние между точками, изображающими
числа
,
т.е. расстояние между точками, изображающими
числа![]() и
и![]() .
.
Найти модуль и главное значение аргумента комплексного числа
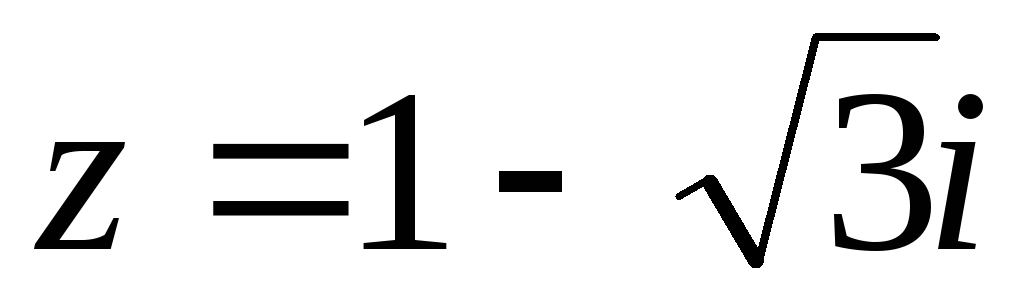 ,
представить его в тригонометрической
и показательной формах.
,
представить его в тригонометрической
и показательной формах.
Решение.
По определению
модуля
![]() .
Так как значения аргумента
.
Так как значения аргумента![]() удовлетворяют соотношению
удовлетворяют соотношению![]() ,
то
,
то![]() .
Итак,
.
Итак,![]() ,
,![]() и согласно (1.6) и (1.12) имеем
и согласно (1.6) и (1.12) имеем![]() ,
,![]() .
.
Для комплексных чисел
 и
и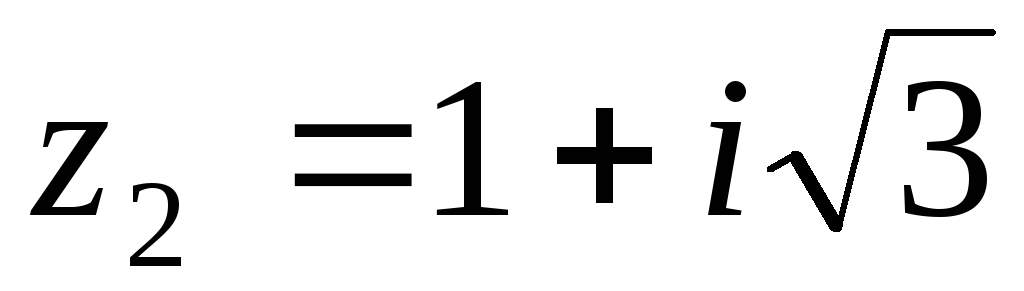 ,
вычислить
,
вычислить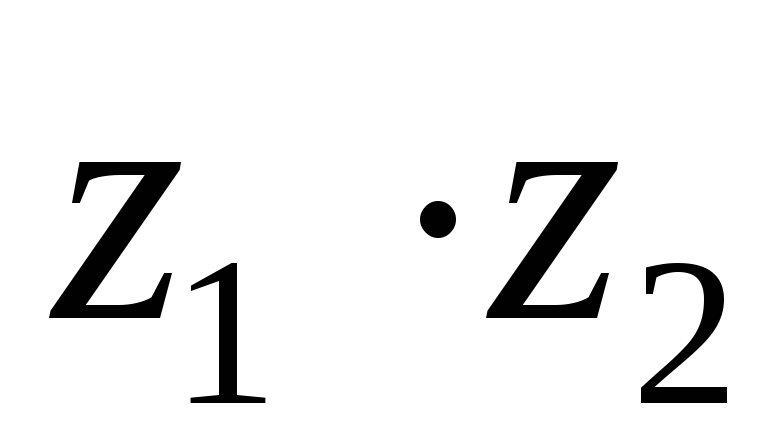 и
и ,
представив их вначале в тригонометрической
форме.
,
представив их вначале в тригонометрической
форме.
Решение.
![]() ,
,
![]() .
Применяя формулы (1.7) и (1.8), получим
.
Применяя формулы (1.7) и (1.8), получим
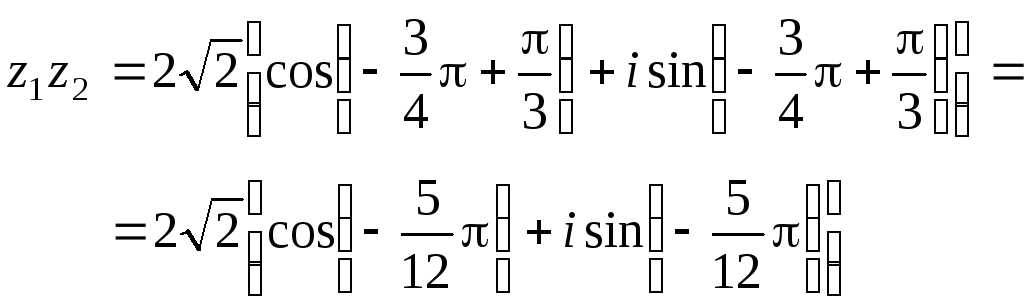
![]()
Вычислить
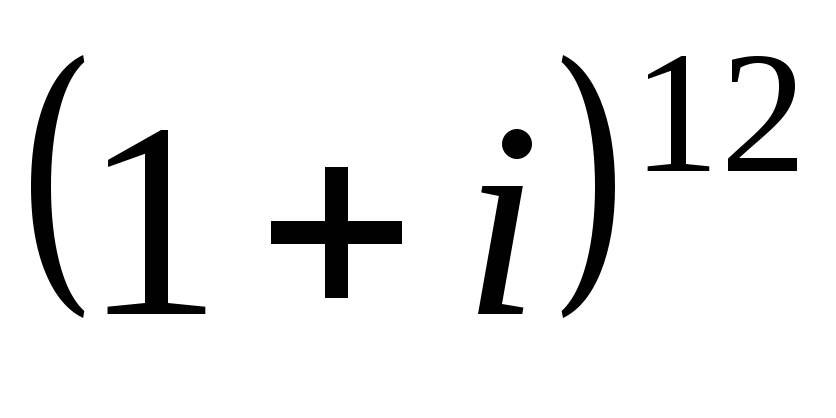 .
.
Решение.
Запишем
число
![]() в тригонометрической форме. По формуле
(1.9) имеем
в тригонометрической форме. По формуле
(1.9) имеем![]()
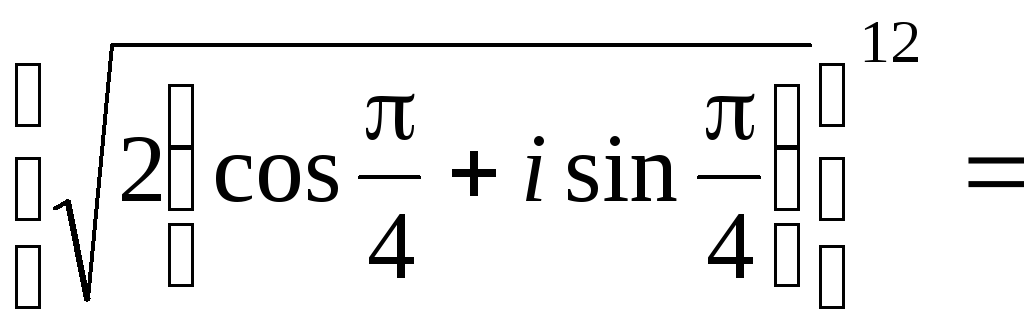
![]() .
.
Вычислить и изобразить на комплексной плоскости все значения
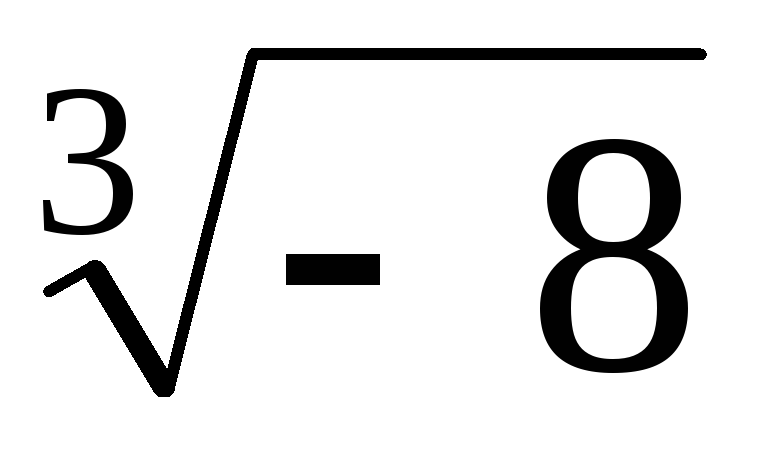 .
.
Решение.
Представим
![]() в тригонометрической форме (1.6), для чего
найдем модуль и главное значение
аргумента
в тригонометрической форме (1.6), для чего
найдем модуль и главное значение
аргумента![]() ,
,![]() .
Имеем
.
Имеем![]() .
.
Применяя
формулу (1.10), найдем 3 значения корня,
содержащихся в формуле
![]() ,
где
,
где![]() .
Воспользовавшись показательной и
тригонометрической формами числа (1.6),
(1.12), получаем
.
Воспользовавшись показательной и
тригонометрической формами числа (1.6),
(1.12), получаем
при
![]()
![]() ,
,
при
![]()
![]() ,
,
при
![]()
![]() .
.
Точки
![]() ,
,![]() ,
,![]() образуют вершины правильного треугольника,
вписанного в окружность радиуса 2 с
центром в начале координат (рис. 1.3).
образуют вершины правильного треугольника,
вписанного в окружность радиуса 2 с
центром в начале координат (рис. 1.3).
Решить уравнение
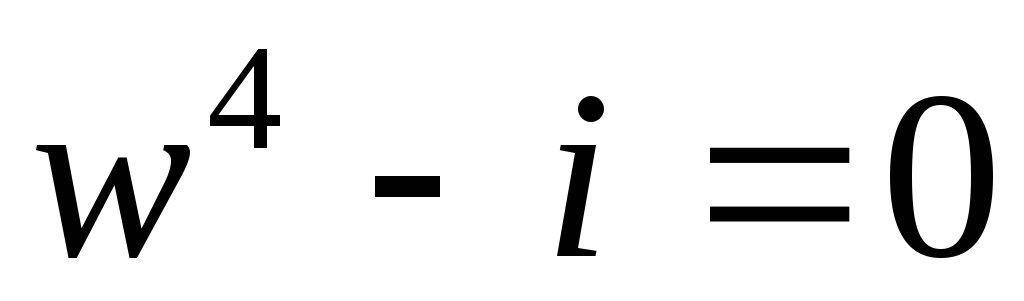 .
.
Решение.
Нахождение
всех корней уравнения сводится к задаче:
найти все значения корня
![]() .
Для чего запишем число
.
Для чего запишем число![]() в показательной форме
в показательной форме![]() и применим формулу (1.16)
и применим формулу (1.16)![]() ,
где
,
где![]()
![]() .
.
При
![]()
![]() ,
откуда следует, что
,
откуда следует, что![]() ,
,![]() .
.
При
![]()
![]() ,
откуда следует, что
,
откуда следует, что![]() ,
,![]() .
.
При
![]()
![]() ,
,![]()
![]() ,
,![]() .
.
При
![]()
![]() ,
,![]()
![]() ,
,![]() .
.
|
|
Рис.1.4 |
Как
видно из рис. 1.4, точки
![]() ,
,![]() ,
,![]() ,
,![]() комплексной плоскости лежат в вершинах
квадрата (на окружности радиуса
комплексной плоскости лежат в вершинах
квадрата (на окружности радиуса![]() с центром в начале координат).
с центром в начале координат).
Упражнения для самостоятельной работы
Выполнить основные четыре действия алгебры над комплексными числами
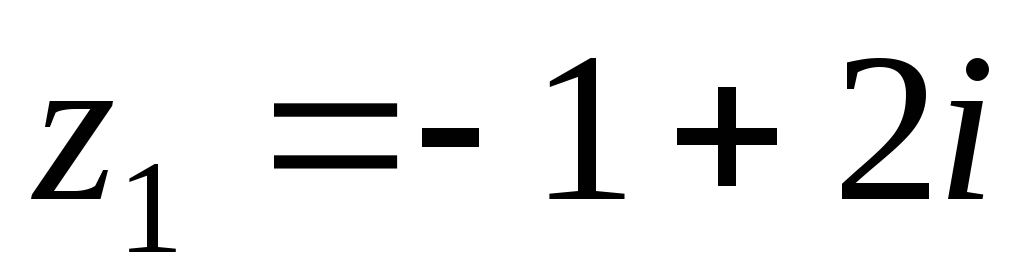 и
и .
.Найти действительные решения уравнения
![]() .
.
Найти середину отрезка, соединяющего точки
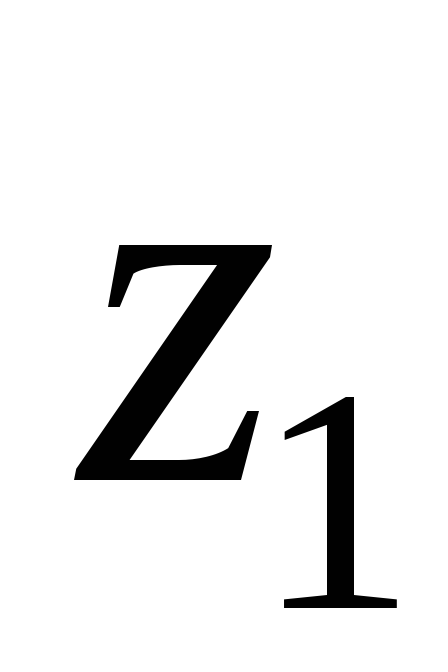 и
и .
.Три последовательные вершины параллелограмма находятся в точках
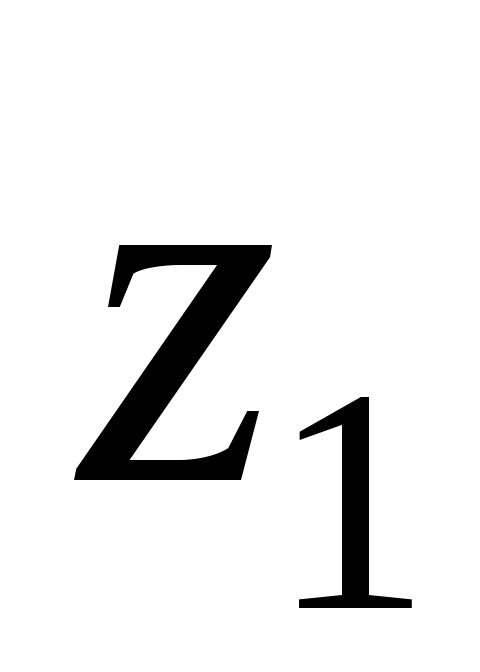 ,
,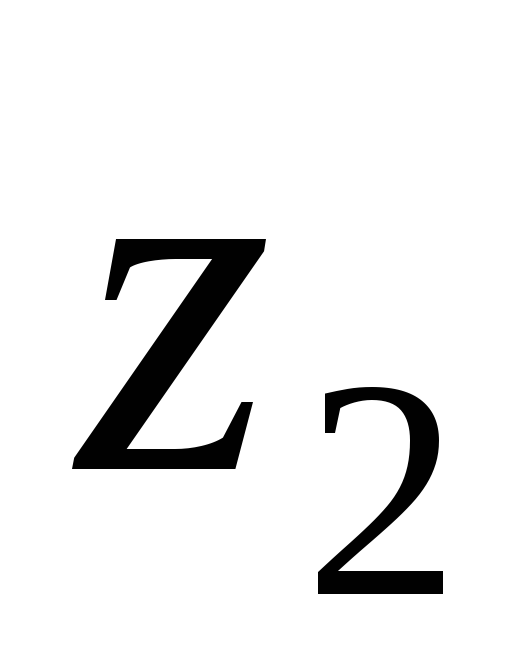 ,
,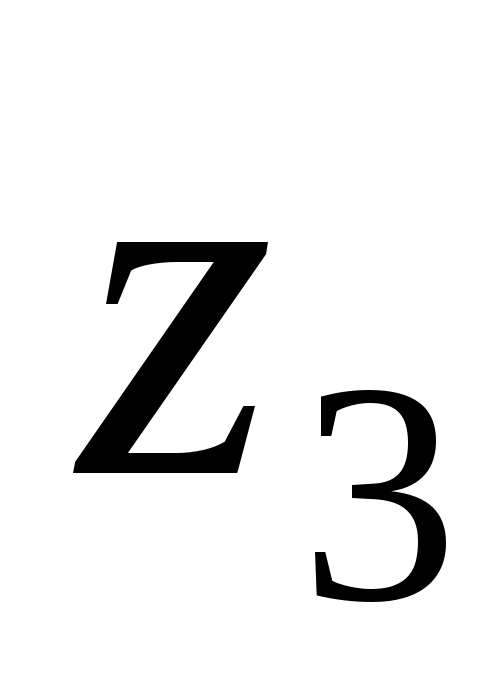 .
Найти четвертую вершину.
.
Найти четвертую вершину.Показать, что
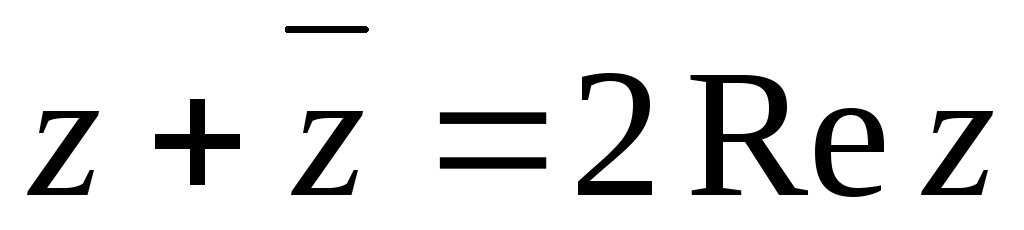 ,
,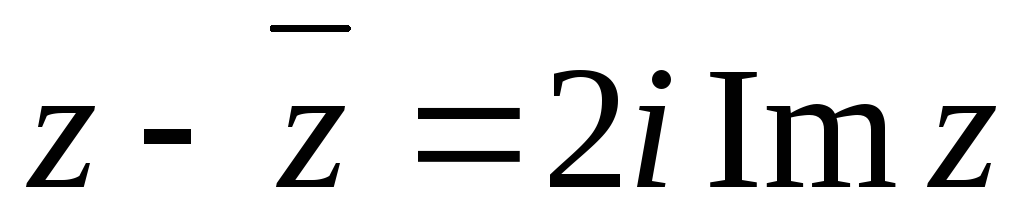 .
.Изобразить на комплексной плоскости числа
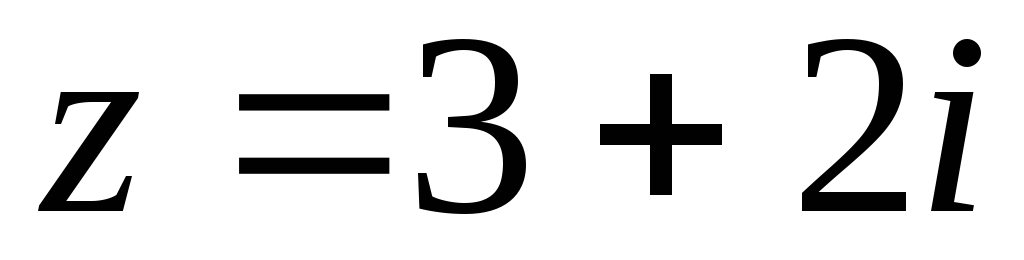 ,
,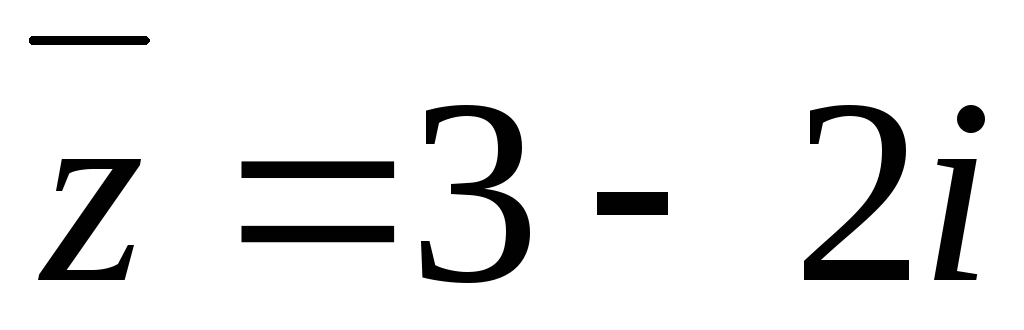 .
Найти их модули и аргументы.
.
Найти их модули и аргументы.Изобразить на комплексной плоскости числа
а)
![]() ; б)
; б)![]() ; в)
; в)![]() ;
;
г)
![]() ; д)
; д)![]() ; е)
; е)![]()
и вычислить их модули и главные значения аргумента.
Представить в показательной форме числа
![]() ;
; ![]() ;
;![]() ;
;![]() .
.
Найти модуль и аргумент числа
 ,
если
,
если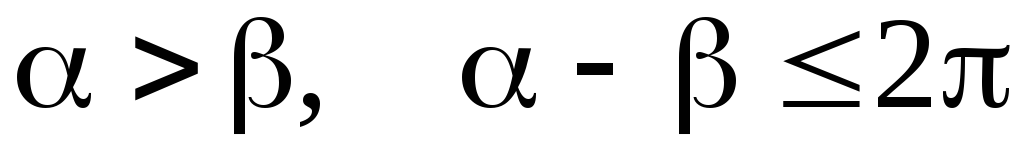 .
.Вычислить
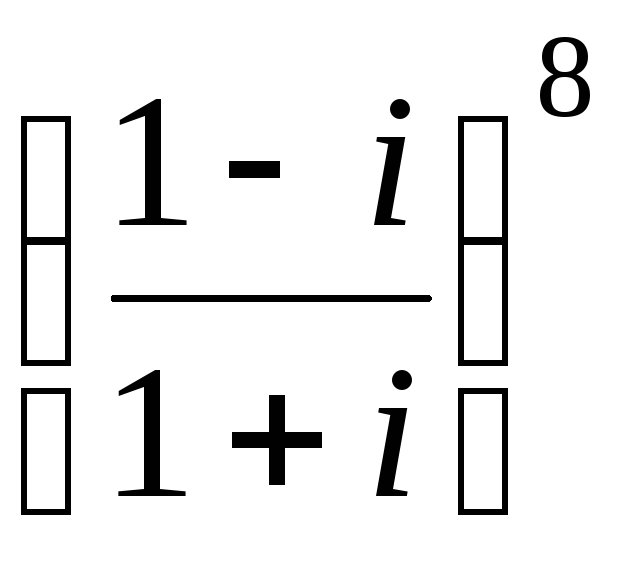 .
.Решить уравнение
 .
.
2. Множества точек, линии, области на комплексной плоскости
Линии и области на комплексной плоскости мы рассматриваем как множество точек, обладающих определенными свойствами и удовлетворяющих определенным уравнениям или системе уравнений, неравенствам или системе неравенств.
Параметрические уравнения кривой в действительных переменных
![]()
в комплексной плоскости могут быть заменены одним уравнением
![]() ,
(2.1)
,
(2.1)
которое называется параметрическим или уравнением кривой в комплексной форме.
Если
кривая задана в неявном виде
![]() ,
то путем подстановки в это уравнение
выражений
,
то путем подстановки в это уравнение
выражений
![]() (2.2)
(2.2)
получим
уравнение кривой в комплексной форме
![]() .
.
При
решении задач по определению и изображению
линии и областей в комплексной плоскости
следует помнить геометрический смысл
модуля разности двух комплексных чисел
![]() (см. упражнение 2). Рассматривая
(см. упражнение 2). Рассматривая
![]() как расстояние между двумя точками
как расстояние между двумя точками
![]() и
и
![]() плоскости, достаточно легко задавать
аналитически линии и области.
плоскости, достаточно легко задавать
аналитически линии и области.

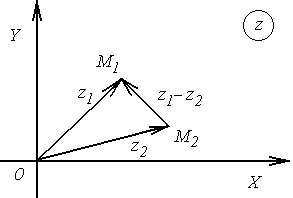
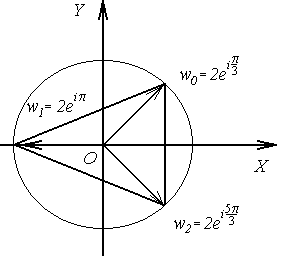 Рис.1.3
Рис.1.3