Контрольная работа 1

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Кафедра программного обеспечения информационных технологий

Факультет ФНиДО

Специальность ПОИТ

Контрольная работа № 1

по дисциплине «ВЫСШАЯ МАТЕМАТИКА»

часть 1

Вариант № 6

Выполнил студент: Бондаренко С.В.

группа 191001

Зачетная книжка № 191001-6

Минск 2011

Основы векторной алгебры и аналитической геометрии

6. Даны четыре векторазаданные в прямоугольной декартовой системе координат.Требуется: 1) вычислить скалярное произведение ; 2) вычислить векторное произведение ; 3) показать, что векторы образуют базис и найти координаты вектора в этом базисе.

Решение: 1) Скалярное произведение векторов вычисляется по формуле

Для заданного случая получаем:

2) Векторное произведение векторов вычисляется по формуле

Для заданного случая получаем:

3)Найдем определитель матрицы, составленной из координат векторов :

Определитель не равен 0, значит векторы образуют базис. Найдем координаты вектора в этом базисе:

Решая эту систему уравнений, получаем:

Таким образом, вектор в базисе векторов будет иметь координаты (-2;4; -3).

16. Даны координаты вершин пирамиды . Найти: 1) длину ребра ; 2) уравнение прямой 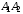; 3) угол между рёбрами и ; 4) уравнение плоскости ; 5) угол между ребром и гранью ; 6) уравнение высоты, опущенной из вершины на грань ; 7) площадь грани ; 8) объём пирамиды; 9) сделать чертёж.

Координаты точек А₁(0; 7; 1), А₂(4; 1; 5), А₃(4; 6; 3), А₄(3; 9; 8).

Решение: 1) Длина ребра А₁А₂ равна длине вектора:

2) Уравнения прямой А₁А₂:

3) Угол между ребрами А₁А₂ и А₁А₄ определим по формуле:

Длина вектора

4) Уравнение плоскости А₁А₂А₃:

Раскрывая определитель и группируя слагаемые, получаем:

5) Угол между ребром А₁А₄ и гранью А₁А₂А₃:

Уравнение грани А₁А₂А₃ найдено в предыдущем пункте:

Вектор имеет координаты (3; 2; 7). Угол между вектором и плоскостью определяется по формуле:

6)Уравнение высоты, опущенной из вершины А₄ на грань А₁А₂А₃:

7) Площадь грани А₁А₂А₃ определим по формуле:

8) Объем пирамиды найдем по формуле:

9) Чертеж пирамиды:

26. Найти координаты точки , симметричной точке относительно плоскости .

Решение: Нормальный вектор заданной плоскости (1,4,3) является направляющим для прямой, на которой находится искомая точка, и эта прямая проходит через точку М. Тогда:

Находим точку пересечения найденной прямой с заданной плоскостью, для чего записываем уравнение прямой в параметрическом виде.

Подставив в уравнение плоскости, получим:

Таким образом, координаты точки Pпересечения найденной прямой с заданной плоскостью равны

Так как эта точка делит отрезок ММ’ пополам, то имеют место следующие соотношения

Таким образом, координаты искомой точки М’(0; -3; -2).

36. Составить уравнение линии, для каждой точки которой расстояния до начала координат и до точки относятся как 3:2. Привести полученное уравнение к каноническому виду и указать тип линии, описываемой этим уравнением.

Решение: Пусть точка М(х; у) лежит на искомой линии. Расстояние от этой точки до начала координат равно , а расстояние от этой точки до точки А(0; 5) равно Таким образом, получаем равенство:

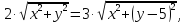
В результате получили каноническое уравнение эллипса с центром в точке (0; 9).