
Часть 1. Контрольная работа №1. Вариант 4
.docx
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Кафедра высшей математики
Факультет ФНиДО
Специальность ПОИТ
Контрольная работа № 1
по дисциплине «Высшая математика»
часть 1
Вариант № 4
Выполнил студент: XXX
группа XXX
Студенческий билет № XXX
Минск 2012
Вариант 4
Задача 4.
Даны четыре вектора a̅ (a1; a2; a3), b̅(b1; b2; b3), c̅(c1; c2; c3) и d̅(d1; d2; d3),
заданные в прямоугольной декартовой системе координат. Требуется:
1) вычислить скалярное произведение b̅·(2 a̅ - c̅);
2) вычислить векторное произведение c̅ × (a̅ - 3b̅);
3) показать, что векторы a̅, b̅, c̅ образуют базис и найти координаты вектора d̅ в этом базисе,
если a̅ = (3; -2; 0); b̅ = (-2; 3; 4); c̅ = (1; 1; -3); d̅ = (11; -9; -11).
Решение:
-
b̅ • (2 a̅ - c̅)
2a̅ = 2 • (3;-2;0) = (6;-4;0)
2a̅ – c̅ = (6;-4;0) – (1;1;-3) = (5;-5;3)
b̅ • (2a̅ - c̅) = (-2;3;4) • (5;-5;3) = -10 + (-15) +12 = -13
-
c̅ × (a̅ - 3b̅)
3b̅ =3 • (-2;3;4) = (-6;9;12)
a̅ – 3b̅ = (3;-2;0) – (-6;9;12) = (9;-11;-12)
c̅
×
(a̅ - 3b̅) =
 =
=
= (1 • (-12) – (-3) • (-11)) i – (1 • (-12) – (-3) • 9) j + (1 • (-11) – 9 • 1) k =
= -45i – 15j -20k
c̅ × (a̅ - 3b̅) = (-45; -15; -20)
-
Докажем, что векторы a̅, b̅, c̅ некомпланарны и образуют базис пространства R3:
(a̅,
b̅,
c̅)
=
 =
=
= 3 • 3 • (-3) + (-2) • 4 • 1 + (-2) • 1• 0 – 1 • 3 • 0 + (-2) • (-2) • (-3) + 1 • 4 • 3 = -35 ≠ 0
Значит, векторы a̅, b̅, c̅ некомпланарны и образуют базис, в котором вектор d̅ может быть представлен в виде линейной комбинации базисных векторов:
d̅ = αa̅ + βb̅ + γc̅
Запишем это равенство в координатном виде:

где α, β, γ - неизвестные координаты вектора d̅ в базисе a̅, b̅, c̅.
Решим систему по формулам Крамера:
Δ
=
 =
-5
=
-5
Δα
=
 = 20
= 20
Δβ
=
 = 40
= 40
Δγ
=
 = -35
= -35
α
=
 =
=
 = -4
= -4
β
=
 =
=
 = -8
= -8
γ
=
 =
=
 = 7
= 7
Значит, d̅ = -4α -8β + 7γ
Задача 14.
Даны
координаты вершин пирамиды
 .
Найти:
.
Найти:
1) длину
ребра
 ;
;
2) уравнение
прямой
 ;
;
3) угол
между рёбрами
 и
и
 ;
;
4) уравнение
плоскости
 ;
;
5) угол
между ребром
 и
гранью
и
гранью
 ;
;
6) уравнение
высоты, опущенной из вершины
 на
грань
на
грань
 ;
;
7) площадь
грани
 ;
;
8) объём пирамиды;
9) сделать чертёж,
если:
 .
.
Решение:

-
Уравнение прямой, проходящей через две точки:

где
(x0,
y0,
z0)
– координаты точки
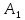 ,
а (x1,
y1,
z1)
– координаты точки
,
а (x1,
y1,
z1)
– координаты точки
 .
Тогда
.
Тогда
уравнение
прямой
 примет
вид:
примет
вид:

В таком виде уравнения прямой называются каноническими. Они могут быть записаны и в виде уравнения прямой как линии пересечения двух плоскостей:
 <=>
<=> 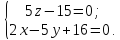
-
Угол ϕ между векторами
 и
и
 вычисляется по формуле:
вычисляется по формуле:

где
в числителе скалярное произведение
векторов
 и
и
 ,
а в знаменателе -произведение их длин.
,
а в знаменателе -произведение их длин.
Находим:
 ;
;
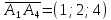 ;
;
| |
=
|
=

| |
=
|
=
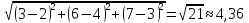
 ,
,
 )
= (
)
= ( )
= 9
)
= 9


-
Уравнение для плоскости
 ,
проходящей через три точки:
,
проходящей через три точки:
 ,
,
где
 - координаты точки
- координаты точки
 ,
,
 -
координаты точки
-
координаты точки
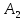 ,
,
 -
координаты точки
-
координаты точки

 <=>
<=>

-
Угол между гранью и ребром определяем из уравнения угла между прямой и плоскостью:

где
n̅
- нормальный вектор плоскости
 ,
a̅
- направляющий вектор прямой
,
a̅
- направляющий вектор прямой
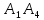
Из
пункта 3 имеем a̅
 ,
из пункта 4 имеем n̅
=
(0;0;21)
,
из пункта 4 имеем n̅
=
(0;0;21)
Таким образом,

Отсюда ϕ = arcsin(4)
-
Искомое уравнение высоты получим из канонических уравнений прямой

где
 – координаты точки, лежащей на
прямой. Пусть это будет точка
– координаты точки, лежащей на
прямой. Пусть это будет точка  (точка вершины пирамиды). m,
n, p
– координаты нормального вектора
плоскости
(точка вершины пирамиды). m,
n, p
– координаты нормального вектора
плоскости
 ,
его значение берем из уравнения плоскости
(пункт 4): n̅ =
(0;0;21)
,
его значение берем из уравнения плоскости
(пункт 4): n̅ =
(0;0;21)
Таким образом,

-
 ,
,



-
 ,
,



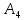





Задача 24.
Найти
координаты точки
 ,
симметричной точке
,
симметричной точке
 относительно
плоскости
относительно
плоскости
 .
.
Решение:
Составим уравнение прямой, проходящей через точку М и перпендикулярную плоскости P:

В качестве направляющего вектора прямой возьмем нормальный вектор плоскости Р:
n̅ = (4;-5;-1)

Запишем уравнение прямой в параметрическом виде:

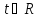
Подставим эти уравнения в уравнение плоскости Р и найдем t:


Значит,

Координаты
точки
 найдем
из формул:
найдем
из формул:







Значит,
точка
 имеет координаты (15;-20;-4)
имеет координаты (15;-20;-4)
Задача 34.
Составить уравнение линии, каждая точка которой находится вдвое ближе к точке A(1;0), чем к точке B(-2;0). Привести полученное уравнение к каноническому виду и указать тип линии, описываемой этим уравнением.
Решение:
Обозначим произвольную точку искомой линии как M(x;y), принадлежащую линии.
Согласно условию, расстояние от точки М до точки B(-2;0) в два раза больше, чем до точки А(1;0):

Преобразуем уравнение:


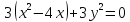



Это каноническое уравнение окружности с центром в точке (2;0) и радиусом 2.




