
Коэффициент стьюдента
Число прямых измерений всегда конечно. Поэтому средняя квадратичная погрешность заведомо меньше истинной абсолютной погрешности. Чтобы получить близкое к реальности значение абсолютной погрешности, нужно увеличить среднюю квадратичную погрешность, умножив ее на коэффициент Стьюдента . В теории Стьюдента рассчитаны значения этого коэффициента в зависимости от доверительной вероятности α и числа измерений n. С ростом доверительной вероятности, то есть надежности значения абсолютной погрешности, коэффициент Стьюдента увеличивается. А с ростом числа измерений, увеличивающим надежность самих результатов измерения, коэффициент Стьюдента уменьшается. Ниже приведены значения коэффициента Стьюдента для доверительной вероятности α = 0,95.
n |
2 |
3 |
4 |
5 |
6 |
tα (n) |
12,71 |
4,303 |
3,182 |
2,776 |
2,571 |
n |
7 |
8 |
9 |
10 |
20 |
tα (n) |
2,447 |
2,365 |
2,306 |
2,262 |
2,093 |
Отметим, что запись результата измерения в форме (7) означает, что значение измеренной величины x с заданной вероятностью α не выйдет за пределы интервала (xср – Δx, xср + Δx). Поэтому абсолютную погрешность Δx
часто называют полушириной доверительного интервала.
Расчет погрешности результатов косвенных измерений
Результат косвенного измерения есть результат расчета по заданной формуле. Оценка относительной погрешности результата расчета уже описана выше. Относительная погрешность рассчитывается по формуле (2), если величины, полученные в результаты прямых измерений, входят в заданную формулу в качестве множителей или делителей.
Для примера рассмотрим косвенное измерение объема прямого цилиндра высоты h с диаметром d. Объем такого цилиндра можно вычислить по формуле
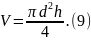
Для вычисления объема цилиндра по формуле (9) нужно иметь результаты измерения его диаметра и высоты. Пусть в результате прямых измерений получены значения диаметра и высоты цилиндра в соответствии с (7):


В этом случае известны и относительные погрешности значений диаметра и высоты цилиндра:
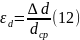
и
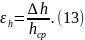
Прежде, чем приступать к вычислению объема, оценим относительную погрешность результата вычисления по формуле (9). В эту формулу входят четыре величины (числа). Два числа из них пришли из математики и являются, а скорее считаются, абсолютно точными: это числа 4 и π. Но число 4 – конечное число, а число π – является бесконечной непериодической дробью. Как это будет показано, можно взять округленное значение числа π с таким количеством значащих цифр, что это число практически не внесет никакой погрешности в окончательный результат расчета значения объема цилиндра.
Таким образом, источниками погрешности являются значения диаметра и высоты цилиндра. Обе эти величины входят множителями в формулу (9), но диаметр входит множителем два раза (в квадрате), а высота – один раз. Следовательно, подстановка этих величин в формулу (9) приведет к сложению двух относительных погрешностей диаметра и одной относительной погрешности высоты. Согласно формуле (2), относительная погрешность объема составит
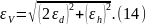
Как видим, наибольший вклад в относительную погрешность объема цилиндра вносит неточность измерения диаметра цилиндра. Поэтому для уменьшения погрешности результата необходимо именно диаметр цилиндра измерить с как можно большей точностью.
Чтобы число π не внесло дополнительную погрешность в результат вычисления объема, нужно взять его значение с относительной погрешностью, много меньшей погрешностей диаметра и высоты цилиндра. Поскольку, как нам известно, точность числа зависит от количества значащих цифр в нем, нужно взять столько цифр числа π, чтобы их количество на одну цифру превышало бы максимальное число значащих цифр в средних значениях диаметра и высоты. Вот запись округленного числа π, содержащая 7 значащих цифр: π = 3,141593.
Теперь, взяв число π с необходимым количеством значащих цифр, можно выполнить расчет среднего значения объема цилиндра по формуле (9):
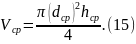
После этого нужно выполнить расчет относительной погрешности значения объема по формуле (14). Затем вычислить абсолютную погрешность объема по формуле

Значение этой погрешности нужно округлить, оставив только две значащие цифры. Затем нужно уточнить запись среднего значения объема, сопоставив его с величиной абсолютной погрешности (16). Число, обозначающее среднее значение объема, нужно округлить, оставив в нем все цифры вплоть до разряда, являющегося последним в окончательной записи абсолютной погрешности. Записываем результат измерений в виде суммы округленного среднего значения и абсолютной погрешности:
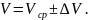
Например, мы
получили следующие величины: среднее
значение
 = 3867,395 мм3,
= 3867,395 мм3,
 = 4,258 мм3.
Округляем значение
до двух значащих цифр, получаем
= 4,3 мм3.
Вторая значащая цифра находится в
разряде десятых долей миллиметра.
Значит, последней оставленной цифрой
в записи
должна быть цифра 3, стоящая в этом же
разряде. Первой отбрасываемой цифрой
является 9 ˃ 5, следовательно, нужно
добавить 1 к оставленной тройке. В итоге
получим: V
= (3867,4
4,3) мм3
= (3,8674
0,0043)
= 4,258 мм3.
Округляем значение
до двух значащих цифр, получаем
= 4,3 мм3.
Вторая значащая цифра находится в
разряде десятых долей миллиметра.
Значит, последней оставленной цифрой
в записи
должна быть цифра 3, стоящая в этом же
разряде. Первой отбрасываемой цифрой
является 9 ˃ 5, следовательно, нужно
добавить 1 к оставленной тройке. В итоге
получим: V
= (3867,4
4,3) мм3
= (3,8674
0,0043)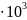 мм3
= (3,8674
0,0043)
мм3
= (3,8674
0,0043)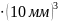 = (3,8674
0,0043)
= (3,8674
0,0043)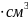 .
Окончательно:
.
Окончательно:
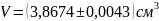
с относительной погрешностью, равной
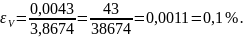
КОЕ-ЧТО ИЗ МАТЕМАТИКИ
Для успешного освоения предлагаемого курса физики нужно вспомнить, что такое вектор и как с ним работать, поскольку в описании физической реальности нельзя обойтись без векторных величин. Многие физические величины являются векторами.
Вектор можно изобразить в виде направленного отрезка определенной длины. Вектор имеет две характеристики: модуль (абсолютную величину или просто величину) и направление. Каждая из этих характеристик может быть постоянной или изменяться независимо от другой.
Векторы складываются по правилу треугольника, как это показано на рисунке.



При умножении вектора на число получается новый вектор, который направлен в ту же сторону, что и старый, если число положительное, и в противоположную сторону, если число отрицательное. Модуль нового вектора равен произведению модуля старого вектора на модуль этого числа.
При умножении вектора на число 0, получается нулевой вектор, не имеющий ни величины, ни направления.
Любой вектор можно спроецировать на ось координат. Проекция вектора на ось координат равна произведению модуля этого вектора на косинус угла между вектором и осью. Если угол острый, то его косинус и соответственно проекция вектора положительны. Если угол тупой, то его косинус и соответственно проекция вектора отрицательны. Если вектор перпендикулярен оси, то его проекция на эту ось равна нулю.
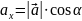
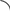
 α
α
0
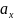

Любой вектор можно представить в виде суммы трех его составляющих по осям координат:
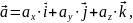
где
,
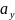 ,
и
,
и
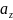 – проекции вектора, а
– проекции вектора, а
 – единичные векторы (орты) соответствующих
осей координат.
– единичные векторы (орты) соответствующих
осей координат.
Вектор
равен сумме трех векторов
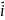 ,
,
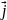 ,
,
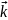 ,
каждый из которых направлен вдоль своей
оси координат.
,
каждый из которых направлен вдоль своей
оси координат.
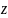

0
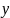
Допустим некоторая
векторная физическая величина, например
скорость
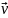 ,
изменилась с течением времени. Тогда
изменение скорости тоже будет вектором:
,
изменилась с течением времени. Тогда
изменение скорости тоже будет вектором:
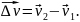
Для нахождения
вектора
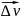 это векторное равенство перепишем
по-другому
это векторное равенство перепишем
по-другому
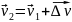
и найдем этот
вектор по правилу треугольника.
Откладываем из одной точки два вектора
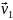 и
и
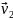 .
По правилу треугольника строим вектор
.
Обратите внимание, какой физический
смысл здесь раскрывается: Вектор
изменения
скорости
соединяет конец первого вектора с концом
второго, то есть показывает, как изменился
вектор скорости (увеличился или уменьшился
и в какую сторону повернулся).
.
По правилу треугольника строим вектор
.
Обратите внимание, какой физический
смысл здесь раскрывается: Вектор
изменения
скорости
соединяет конец первого вектора с концом
второго, то есть показывает, как изменился
вектор скорости (увеличился или уменьшился
и в какую сторону повернулся).
Существуют два разных умножения вектора на вектор: скалярное и векторное.
Результатом скалярного произведения вектора на вектор является число, равное произведению модуля первого вектора на модуль второго и на косинус угла между ними:
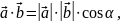
или равное сумме одноименных проекций этих векторов на оси координат:
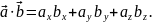
Скалярное умножение обозначается точкой.
Результатом векторного произведения вектора на вектор является вектор. Векторное умножение обозначается косым крестиком. Например, вектор равен векторному произведению векторов и :
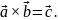
Вектор перпендикулярен векторам и и его направление определяется по правилу буравчика (правого винта), как это показано на рисунке. Буравчик вращается от первого вектора в сторону второго вектора . Если векторы – множители поменять местами, то вектор изменит направление на противоположное.
Модуль вектора равен произведению модуля первого вектора на модуль второго и на синус угла между ними:
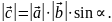

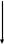

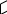


α
Если два вектора
параллельны, то их векторное произведение
равно нулевому вектору
 .
.
Для успешного освоения предлагаемого курса физики нужно также вспомнить основы математического анализа и, как минимум, уметь найти производную от комбинации элементарных функций и взять табличный интеграл.
Напомню определение производной. Пусть некоторая физическая величина, например вектор скорости, меняется с течением времени. Тогда время t является независимой переменной, то есть аргументом (играет роль x из математики). А скорость является зависимой переменной, то есть функцией (играет роль y из математики). Производной называется предел
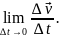
Если
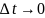 ,
то и
,
то и
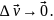 Существует обозначение для величины,
которая стремится к 0, но не равна 0. Эта
величина называется бесконечно малой.
Все дело в том, что она
не имеет конкретного значения.
Зато она всегда меньше любого сколь
угодно малого числа, какое бы мы ни
назвали. Для такой бесконечно малой
величины существует обозначение:
Существует обозначение для величины,
которая стремится к 0, но не равна 0. Эта
величина называется бесконечно малой.
Все дело в том, что она
не имеет конкретного значения.
Зато она всегда меньше любого сколь
угодно малого числа, какое бы мы ни
назвали. Для такой бесконечно малой
величины существует обозначение:
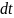 .
Это выражение называется дифференциалом
и является в данном случае бесконечно
малым промежутком времени.
.
Это выражение называется дифференциалом
и является в данном случае бесконечно
малым промежутком времени.
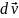 – бесконечно малое приращение вектора
скорости. Имеем дробь:
– бесконечно малое приращение вектора
скорости. Имеем дробь:
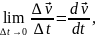
которая обладает всеми свойствами дроби из математики, за исключением того, что ее значение нельзя получить обычным делением числителя на знаменатель, а нужно перейти к пределам и раскрыть получившуюся неопределенность. Для любой функции в математике это все проделано и сведено в правила взятия производной от элементарной функции.
Например, некоторое тело движется так, что модуль его скорости зависит от времени по уравнению:
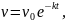
где
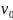 и
и
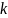 – константы. Найдем производную от
модуля скорости по времени:
– константы. Найдем производную от
модуля скорости по времени:
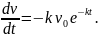
Как Вы вероятно помните, эта производная является ускорением.
Настоятельно рекомендую каждую производную от функции y по аргументу x, которая встретится Вам в физике, обозначать только такой дробью:
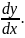
Для успешного
освоения предлагаемого курса физики
нужно также вспомнить, что такое степень
и логарифм.
Степенью называется двухуровневое
выражение вида
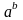 ,
нижняя и верхняя части которого
неравнозначны.
,
нижняя и верхняя части которого
неравнозначны.
Показатель степени
 Степень
Степень
b
a
Основание степени
Для удобства обозначим эту степень буквой у. Имеем равенство
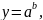
где а – основание степени у, а b – показатель степени у. Чтобы выразить а и b из этого равенства, нужно применить разные правила.
Основание а степени у равно корню из этой степени:
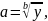
а показатель b степени у равен логарифму этой степени по основанию а:
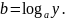
Итак, показатель степени и логарифм степени – это практически одно и то же.
Чтобы убедиться, проверьте тождество:
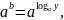
и левая и правая части которого равны у.
