10

Векторный анализ. Скалярное и векторное поле.

Рассмотрим пространственную область(V).Предположим, что в каждой точке P области (V) задано некоторое число u. В этом случае говорят, что в области задано скалярное поле. Если ввести систему координат, то положение точки будет определяться ее координатами, и тогда задание скалярного поля будет равносильно заданию функции трех переменных (или двух, если область плоская) u = u(x, y, z).

MMmm P(x, y, z)→u

(V)

. Примером скалярного поля является поле температур или поле электрического потенциала.

Если в каждой точке области задан вектор F, то говорят, что в области задано векторное поле. Примером векторного поля является поле сил или поле скоростей частиц текущей жидкости.

Производная по направлению.

Рассмотрим функцию z = f(x, y), определенную в некоторой области плоскости (x, y). y

S

Δy Δs M (x+Δx, y+Δy)

β α Δx

M(x,y)

x

Рассмотрим точку M(x, y) и некоторый вектор S, проходящий через эту точку и имеющий направляющие косинусы cos α и cos β На векторе S возьмем точку M₁(x + Δx, y + Δy). Функция z = f(x, y) получит приращение Δz. Будем считать, что функция z и ее производные z′_x и z′_y непрерывны в области, содержащей точки М и М₁, тогда

Если u = u(x, y, z), то

П р и м е р

.Найти производную функции u = x² + y² + z² в направлении вектора s = i + j + k  в точке М(1, -1, 1).

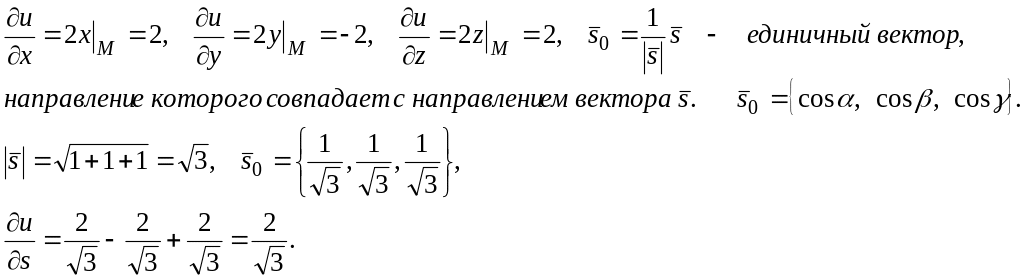
Производная по направлению показывает скорость изменения функции в направлении вектора s.

Градиент.

Рассмотрим функцию u = u(x, y, z) .

называется градиентом функции u = u(x, y, z).

Функции u = u(x, y, z) определяет в пространстве скалярное поле, grad u определяет векторное поле. Таким образом, скалярное поле порождает векторное поле – поле градиента.

На плоскости для функции z = f(x, y)

Теорема.

П роизводная функции u(x, y, z) в направлении вектора s равна проекции градиента функции u на вектор s.

Доказательство.

s ₀ – единичный вектор, направление которого совпадает с направлением вектора s.

|s₀| = 1 s₀ = cos α ∙i + cosβ∙j + cosγ ∙ k. Тогда

grad u

      )φ s₀ s

^∂u/_∂s

Следствие.

Производная по направлению имеет наибольшее значение, если это направление совпадает с направлением градиента.

       

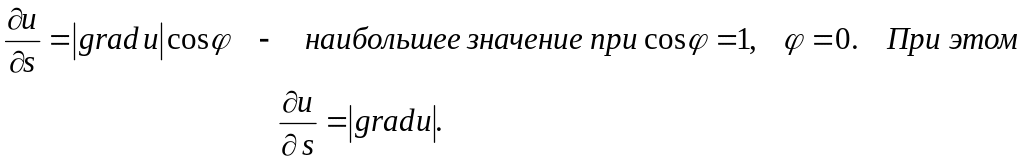
Поток вектора через поверхность.

Пусть в некоторой области (V) задано векторное поле

F(P) = X(x,y,z) i + Y(x,y,z) j + Z(x,y,z) k

(или F(P) = {X(P), Y(P), Z(P)})

Примером векторного поля является поле градиента.

Векторной линией называется линия, которая в каждой точке касается вектора поля.

В области (V) рассмотрим поверхность (S). В каждой точке P поверхности задается положительное направление нормали с единичным вектором n₀(P).

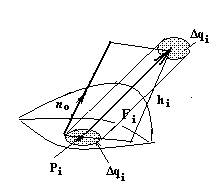
Введем понятие потока вектора через поверхность, рассмотрев некоторую гидромеханическую задачу.

Будем интерпретировать данное поле как поле скоростей частиц текущей несжимаемой жидкости и найдем количество жидкости, протекающей через поверхность в единицу времени. Разобьем поверхность произвольным образом на частичные ячейки ∆q_i. Тогда количество жидкости, протекающей через эту ячейку в единицу времени имеет вид

∆V_i ∆q_i h_i = .

Объем через всю поверхность будет равен

Отсюда

П =

n₀ = {cos α, cos β, cos γ} – направляющие косинусы вектора n.

П = .

Количество жидкости, протекающее через поверхность (S) в единицу времени, равно потоку вектора скорости через поверхность (S) в выбранном направлении.

Если поверхность замкнутая, то поток измеряет общее количество жидкости, протекающее через поверхность (S) в единицу времени в направлении внешней нормали, т. е. поток измеряет силу источников, расположенных внутри поверхности (или стоков, если П < 0)

В общем случае поток определяет количество векторных линий, проходящих через поверхность в единицу времени.