4 БУЛЕВЫ ФУНКЦИИ И ПРЕОБРАЗОВАНИЯ
4.1 Цель занятия
Ознакомление на практических примерах с основными понятиями булевой алгебры. Изучение способов задания булевых функций. Анализ формул и тождеств, которые определяют свойства операций булевой алгебры. Изучение и использование методов доказательства тождеств булевой алгебры.
4.2 Методические указания по организации самостоятельной работы студентов
4.2.1 При подготовке к практическому занятию необходимо повторить лекционный материал, теоретический материал, представленный в пункте 4.2.2 настоящих методических указаний, соответствующие разделы литературы [1-10] по следующим вопросам:
булевы переменные и функции (основные понятия);
область определения и область значений булевой функции;
способы задания булевых функций;
реализация булевых функций формулами;
принцип двойственности в булевой алгебре;
булевы алгебры, законы и тождества булевой алгебры.
Подготовка и выполнение практического занятия проводится в два этапа. Первый этап связан с изучением на практических примерах следующих основных понятий и определений булевой алгебры: булевы переменные; булевы функции; интерпретация булевой функции; n-мерный булев куб; область определения булевой функции; таблица истинности (соответствия) булевой функции; отрицание, конъюнкция, дизъюнкция, эквиваленция, импликация, стрелка Пирса, штрих Шеффера; булева формула; суперпозиция булевых функций; инфиксная запись формул; эквивалентные формулы; двойственная функция; самодвойственная функция; принцип двойственнойсти; двухэлементная булева алгебра; алгебра логики.
При выполнении первого этапа обучаемый должен предложить и записать индивидуальный пример для каждого из рассмотренных выше понятий и определений.
Второй этап выполнения практического занятия связан с решением практических заданий, представленных в подразделе 4.3 на основе предложенных типовых примеров (см. раздел 4.4).
4.2.2 Основные теоретические положения по изучаемой теме.
4.2.2.1 Основные понятия и определения. Булевы переменные и функции.
Рассмотрим основные понятия и определения алгебры логики.
Пусть задано
двухэлементное множество
и двоичные переменные, принимающие
значения из
.
Элементы
часто обозначают 0 и 1, однако они не
являются числами в обычном смысле.
Наиболее распространенная интерпретация
двоичных переменных – логическая: «нет»
– «да», «истинно» (и) – «ложно» (или),
«false»
– «true».
Будем считать, что
,
рассматривая 0 и 1 как формальные символы,
не имеющие арифметического смысла.
Определение.
Переменные, которые могут принимать значения только из множества , называются булевыми или логическими переменными. Элемент 1 называется единичным элементом, или единицей; элемент 0 называется нулевым элементом, или нулем. Сами значения 0 и 1 называются булевыми константами.
Пример.
Булевыми переменными, которые способны принимать лишь два различных значения, характеризуются объекты с двумя возможными состояниями (наличие или отсутствие у объекта определенного признака, низкое или высокое напряжение, истинное или ложное высказывание).
Пример.
В языках
программирования для работы с такими
переменными, как правило, вводится
специальный логический тип (например,
в языках Pascal
и Java
boolean,
в
bool).
Переменная этого типа принимает два
значения «false»
и «true».
Отношения между
булевыми переменными представляются
булевыми
функциями,
которые подобно числовым функциям могут
зависеть от одной, двух и, вообще,
переменных (аргументов).
Определение.
Функция вида
,
аргументы
и значения
которой принадлежат множеству
,
называется
-местной
булевой
(переключательной,
логической)
функцией.
Важнейшая особенность булевых функций состоит в том, что они, как и их аргументы, принимают свои значения из двухэлементного множества , т.е. характеризуются одним из двух возможных состояний.
Пример.
В вычислительной технике булевы функции применяются для описания алгоритмов, средств вычислительной техники – дискретных устройств. Дискретные устройства предназначаются для преобразования дискретной информации, разлагающейся на элементарные единицы – биты. Биты в устройствах реализуются сигналами, которые описываются двоичными переменными – булевыми.
Определение.
Совокупность
конкретных значений аргументов булевой
функции называется кортежем,
двоичным
словом (
-словом)
или булевым
набором длины
и обозначается как
.
Для булевой функции
конкретное (индивидуальное) значение
булевого набора
называется также интерпретацией
булевой функции
f.
Пример. Для
булевой функции
кортежами являются следующие совокупности
конкретных значений аргументов:
,
,
,
;
для булевой функции
кортежами являются:
,
,
,
и т.д.
4.2.2.2 Область определения и область значений булевой функции.
Определение.
Множество всех
двоичных слов, обозначаемое как
,
называется n-мерным
булевым кубом
и содержит
элементов-слов, т.е.
.
Пример.
В множество двоичных
слов для булевой функции
входит
слова: (0) и (1); в множество двоичных слов
для булевой функции
входит
слов:
,
,
,
,
,
,
,
.
Определение.
Областью
определения булевой функции
от
-переменных
служит множество слов длины
,
которые представляют собой всевозможные
наборы из
двоичных цифр и их общее количество
равно
.
Определение.
Функция, зависящая от аргументов, является полностью определенной, если указаны её значения для всех наборов (кортежей, слов) значений элементов.
Пример.
Булева функция от
двух элементов является полностью
определенной, если указаны её значения
для каждого из четырех возможных наборов
(
),
функция трех аргументов – на 8 (
)
наборах также будет полностью определенной.
Теорема. Число
всех функций, зависящих от
переменных
,
равно
.
Действительно,
булева функция
аргументов определена на
наборах, на которых она может принимать
«0» или «1» из общего количества
.
Поэтому в соответствие каждой булевой
функции можно поставить
-разрядное
двоичное число. Но количество различных
-разрядных
чисел равно
,
а следовательно и количество различных
булевых функций равно
.
Пример. От
двух аргументов
существует 16 булевых функций, т.е.
;
от трех – 256 (
),
от четырех – 65536 функций (
).
4.2.2.3 Способы задания булевых функций.
Существует четыре способа задания булевой функции:
вербальный (словесный);
табличный (с помощью таблицы истинности);
порядковым номером, который имеет функция;
аналитический (в виде формулы).
Задание булевых
функций при помощи таблиц.
Булевы функции можно задавать с помощью
таблиц, подобных таблицам сложения и
умножения одноразрядных чисел. В левой
части такой таблицы перечисляются все
наборов значений переменных (булевых
наборов длины
),
а в правой части − значения функций на
этих наборах. Этот способ задания
универсален, т.е. пригоден для любой
функции, однако громоздок, поэтому
применяется для задания функции
небольшого числа переменных.
Определение.
Таблицы, в которых каждой интерпретации (то есть набору аргументов) функции поставлено в соответствие её значение, называются таблицами истинности (соответствия) булевой функции.
В таблице истинности
каждой переменной
и значению самой функции
соответствует по одному столбцу, а
каждой интерпретации
по одной строке. Интерпретации расположены
в определенном порядке − лексикографическом,
который совпадает с порядком возрастания
наборов, рассматриваемых как двоичные
числа.
Пример.
Таблица истинности
функции
может иметь следующий вид (таблица 4.1).
Таблица 4.1 – Пример таблицы истинности функции
-
0
0
0
0
0
0
1
1
0
1
0
0
0
1
1
1
1
0
0
1
1
0
1
1
1
1
0
0
1
1
1
0
В столбцах 1, 2, 3 даны все возможные кортежи значений трех аргументов, т.е. сочетание нулевых и единичных значений трех аргументов. В столбце 4 – значения функции .
Рассмотрим булевы функции, которые зависят от одной и двух переменных.
Булевы функции,
которые зависят от одной переменной,
приведены в таблице 4.2 (их количество
равно
).
Таблица 4.2 Таблица истинности для булевых функций одной переменной
-
0
0
0
1
1
1
0
1
0
1
Две функции
и
представляют собой функции-константы:
является
абсолютно ложной (константа нуля);
является
абсолютно истинной (константа единицы).
Функция
(функция повторения аргумента) повторяет
значения переменной
и поэтому просто совпадает с ней. Функция
,
называемая отрицанием
или инверсией
(
читается «не
»),
является единственной нетривиальной
функцией. Она равна 1, когда аргумент
принимает значение 0, и равна 0 при
аргументе 1.
Всевозможные
булевы функции двух переменных
представлены в таблице 4.3 (их количество
равно
).
Таблица 4.3 Таблица истинности для булевых функций двух переменных
-
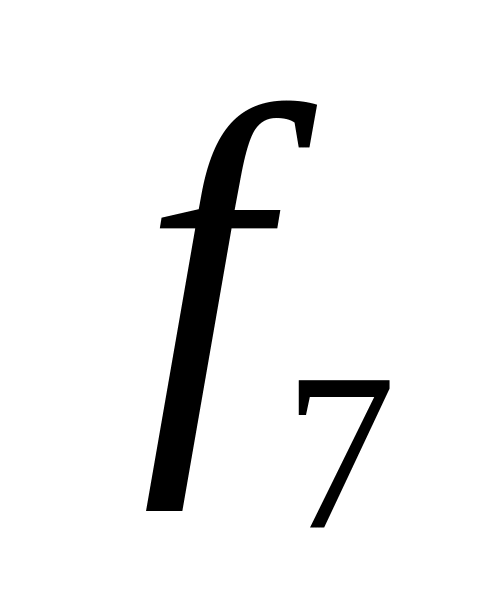
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
0
1
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
1
0
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
1
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
В таблице 4.4 приведена характеристика булевых функций двух переменных.
Таблица 4.4 Характеристика булевых функций двух переменных
Функция |
Обозначения (другие обозначения) |
Названия |
Чтение |
|
0 |
Константа 0 (тождественный нуль, всегда ложно) |
Константа 0 (Любое 0) |
|
( (AND, И) |
Конъюнкция (произведение, пересечение, логическое «и») |
(и и ). Истинна тогда, когда истинны обе переменные |
|
( (>) |
Отрицание импликации (запрет) |
|
|
|
Повторение (утверждение) первого аргумента |
Как
|
|
( |
Отрицание обратной импликации |
Не , но |
|
|
Повторение второго аргумента |
Как |
|
( |
Сумма по модулю 2 (неравнозначность, антиэквивалетность) |
не как (или или ). Истинна, когда истинны или , или в отдельности |
|
( (OR, ИЛИ) |
Дизъюнкция (логическая сумма, логическое «или») |
( или хотя бы ). Истинна тогда, когда истинны или , или , или обе переменные |
|
( |
Стрелка Пирса (функция Вебба, отрицание дизъюнкции) |
Не и не . Истинна только тогда, когда и ложны |
|
( (Eqv) |
Эквиваленция (равнозначность, эквивалентность) |
( , если, и только если ) |
|
( |
Отрицание (инверсия) второго аргумента |
Не |
|
( |
Обратная импликация (обратное разделение с запретом) |
Если , то ( или не ) |
|
( |
Отрицание (инверсия) первого аргумента |
Не |
|
( (Imp) |
Импликация (следование, селекция) |
Если , то (не или ). Ложна тогда и только тогда, когда истинна и ложна |
|
( |
Штрих Шеффера (отрицание конъюнкции, несовместимость, логическое «не-и») |
Не или не . Ложна только тогда, когда и истинны |
|
1 |
Константа 1 (тождественная единица, всегда истинно) |
Константа 1 (Любое 1) |
)
и
)
,
но не
)
)
)
или
)
)
как
)
)
)
)
)
Шесть из приведенных
функций не зависят от
или
(или от обоих вместе). Это две константы
(
и
),
повторения (
,
)
и отрицания (
и
),
являющиеся функциями одной переменной
(
или
.)
Из остальных десяти функций две (
и
)
отличаются от соответствующих им (
и
)
лишь порядком расположения элементов
и поэтому не являются самостоятельными.
Поэтому из 16 функций двух переменных
только восемь являются оригинальными
(
).
В математической
логике часто употребляются так называемые
элементарные функции, которые играют
такую же важную роль, как, например,
или
в математическом анализе. Элементарные
логические функции – это одноместные
и двухместные логические функции.
Примеры элементарных функций одной переменной приведены в таблице 4.2.
Примеры элементарных
функций двух переменных представлены
в таблицах 3.3 и 3.4, это: отрицание
(
);
дизъюнкция
;
конъюнкция
;
импликация
;
эквивалентность
;
сумма по модулю 2
;
штрих Шеффера
;
стрелка Пирса
.
Булевы функции можно рассматривать как логические операции над величинами, принимающими два значения – 0 и 1. Основными в двузначной логике являются три функции:
отрицание (функция , принимающая значения 1, когда
,
и значение 0, когда
);дизъюнкция (функция
,
принимающая значение 0 тогда и только
тогда, когда оба аргумента имеют значение
0);конъюнкция (функция
,
принимающая значение 1 тогда и только
тогда, когда оба аргумента имеют значение
1).
Задание булевой
функции порядковым номером.
Каждой функции присваивается порядковый
номер в виде натурального числа, двоичный
код которого представляет собой столбец
значений функции в таблице истинности.
Младшим разрядом считается самая нижняя
строка (значение функции на интерпретации
,
а старшим
самая верхняя (значение функции на
интерпретации
).
Указанный порядковый номер функции,
как двоичный, так и десятичный, полностью
определяет булеву функцию.
Часто для упрощения записи булевой функции вместо полного перечисления интерпретаций используют только двоичные значения наборов, для которых функция принимает единичные значения. Такую форму записи называют числовой.
Пример.
Найдем порядковый
номер функции
,
которая задана таблицей истинности
(см. табл. 3.1). Для этого переведем двоичное
число
в десятичную систему счисления:
Кортеж значений
аргументов (интерпретацию) также можно
рассматривать как запись целого
положительного числа в двоичной системе
счисления. Первая интерпретация в
таблице истинности называется нулевой,
последняя – единичной (номер интерпретации
,
где
– количество аргументов функции).
Определение.
Десятичный эквивалент двоичного представления интерпретации называется номером интерпретации (кортежа).
Пример.
Шестой интерпретацией
является
,
т.е.
.
Пример.
Пусть функция
принимает единичные значения на
интерпретациях 1, 4, 7. Тогда, используя
числовую форму записи, функция будет
иметь вид:
,
что означает, что функция принимает
единичные значения на наборах 1, 4 и 7.