БГУИР

Факультет непрерывного и дистанционного обучения

Кафедра ВМиП

Курсовая работа по программированию на тему

«Решение СЛАУ методами простой итерации и Зейделя»

Выполнил:

Ст. гр. 702421

Пилипенко О.В.

Проверил:

Старший преподаватель

Навроцкий А.А.

Минск

2010

Содержание

1. Введение…………………………………………………………………………3

2. Условие поставленной задачи, общие теоретические сведения………..…....5

3. Используемые методы решения……………………………………………......7

4. Математическая модель: описание, блок-схема алгоритма программы……21

5. Выводы……………………………………………………………………….....23

6. Литература……………………………………………………………………...25

7. Приложение 1……………………………………………………………….. ...26

1. Введение

Способы решения линейных систем уравнений разделяют на 2 группы.

Первые, точные методы представляющие собой конечные алгоритмы для вычисления корней системы (таковыми например, являются правило Крамера, метод Гаусса, метод главных элементов, метод квадратных корней и др.).

Вторые, итерационные методы позволяющие получить корни системы с заданной точностью путем сходящихся бесконечных процессов (к числу таковых относят, метод итераций, метод Зейделя, метод релаксации).

Вследствие неизбежных округлений результаты даже точных методов являются округленными, причем оценка погрешностей корней в общем случае затруднительна.

При использовании итерационных процессов, сверх того, добавляется погрешность метода.

Заметим, что эффективное применение итерационных методов существенно зависит от удачного выбора приближения и быстроты итерационного процесса.

Сейчас разберем несколько определений которые будем использовать в этой работе.

Система линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида

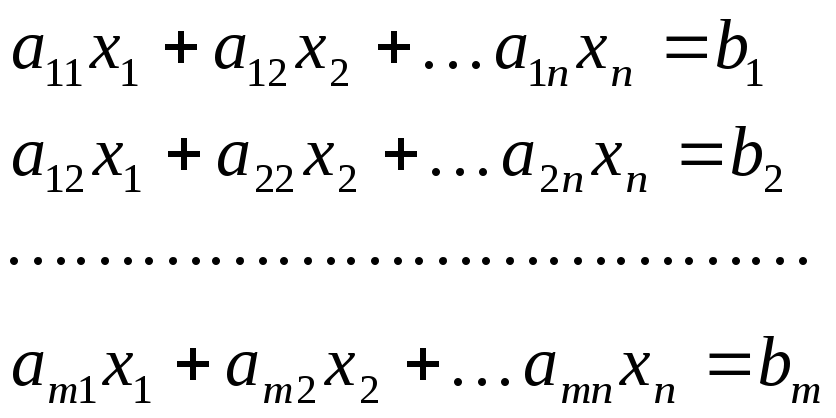(1)

Здесь — неизвестные, которые надо определить. — коэффициенты системы — и — свободные члены — предполагаются известными. Индексы коэффициентов () системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно.

Система (1) называется однородной, если все её свободные члены равны нулю (), иначе — неоднородной.

Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.

Решение системы (1) — совокупность n чисел , таких что подстановка каждого ci вместо xi в систему (1) обращает все ее уравнения в тождества.

Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее нет ни одного решения.

Совместная система вида (1) может иметь одно или более решений.

Решения исовместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:

=соответственно

Совместная система вида (1) называется определенной, если она имеет единственное решение; если же у нее есть хотя бы два различных решения, то она называется неопределенной. Если уравнений больше, чем неизвестных, она называется переопределённой.

2. Условие поставленной задачи, общие теоретические сведения

Выделяют четыре основные задачи линейной алгебры: решение СЛАУ, вы-

числение определителя матрицы, нахождение обратной матрицы, определение

собственных значений и собственных векторов матрицы. Задача отыскания решения СЛАУ с n неизвестными – одна из наиболее часто встречающихся в практике вычислительных задач, так как большинство методов решения сложных задач основано на сведении их к решению некоторой последовательности СЛАУ. Методы решения СЛАУ делятся на прямые и итерационные.

Прямые методы дают в принципе точное решение (если не учитывать ошибок округления) за конечное число арифметических операций. Для хорошо обусловленных СЛАУ небольшого порядка n ≤ 103 − 104 применяются практически только прямые методы. Наибольшее распространение среди прямых методов получили метод Гаусса для СЛАУ общего вида, его модификация для трехдиагональной матрицы метод прогонки и метод квадратного корня для СЛАУ с симметричной матрицей.

Итерационные методы выгодны для систем большого порядка n > 1000, а также для решения плохо обусловленных систем. Многообразие итерационных методов решения СЛАУ объясняется возможностью большого выбора рекуррентных последовательностей, определяющих метод. Наибольшее распространение среди итерационных методов получили одношаговые методы простой итерации и Зейделя с использованием релаксации.

Методы простой итерации и Зейделя сходятся примерно так же, как геометрическая прогрессия со знаменателем G . Если норма матрицы G близка к 1, то сходимость очень медленная. Для ускорения сходимости используется метод релаксации. Суть его в том, что полученное по методу простой итерации или Зейделя очередное значение пересчитывается по формуле:

Здесь 0 < ω ≤ 2 – параметр релаксации.

Если ω < 1 – нижняя релаксация, если ω > 1 – верхняя релаксация. Параметр

ω подбирают так, чтобы сходимость метода достигалась за минимальное число

итераций.

Условия задания.

Составить программу решения СЛАУ порядка n и решить систему линейных

уравнений пятого порядка с трехдиагональной симметричной матрицей вида

методом простой итерации Значения q =(-3.14) , и d = 7 заданы. Построить график зависимости количества итераций it, необходимых для достижения заданной точности, от параметра релаксации ω и установить, при каком значении ω число итераций минимально. Параметр релаксации менять от 0.2 до 2 с шагом 0.2.

3. Используемые методы решения Метод итераций

При большем числе неизвестных Линейная система (ЛС впоследствии) схема метода Гаусса, дающая точное приближение, становиться весьма сложной.

В этих условиях для нахождения корней системы иногда удобнее использовать приближенные методы вычисления. Изложим здесь один из из этих методов – метод итераций.

Пусть дана ЛС

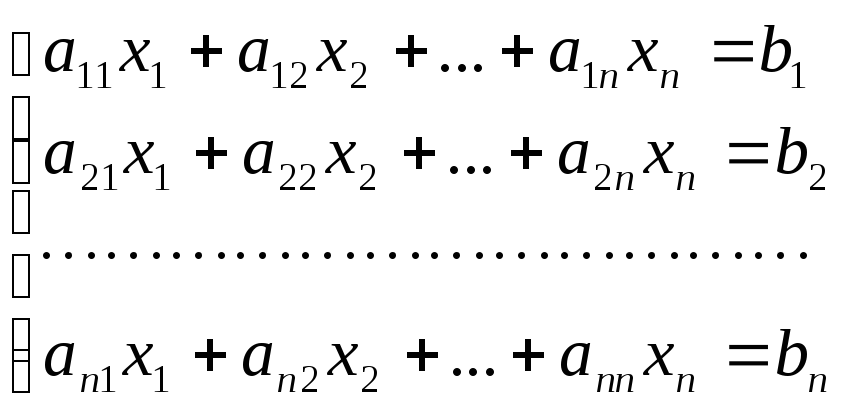
Введя в рассмотрение матрицы

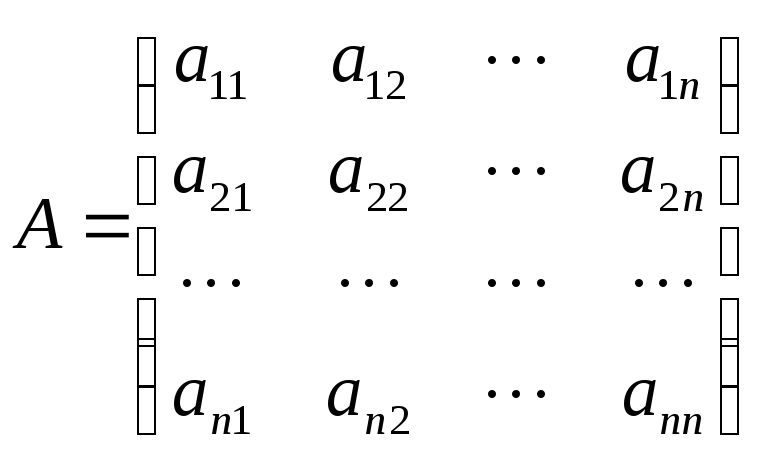
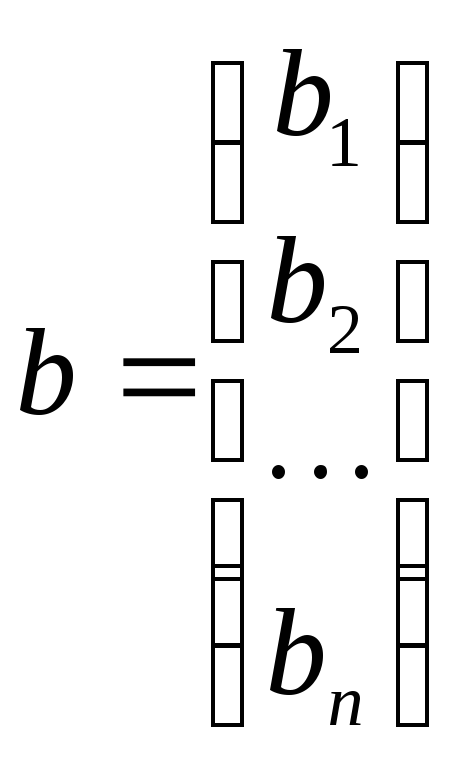(1)

Систему 1 коротко можно записать в виде матричного уравнения

(1’)

Предполагая, что диагональные коэффициенты

Разрешим первое уравнение первое уравнение системы (1) относительно , второе относительно и т. д. Тогда получим эквивалентную систему

(2)

где при

и при

введя матрицы

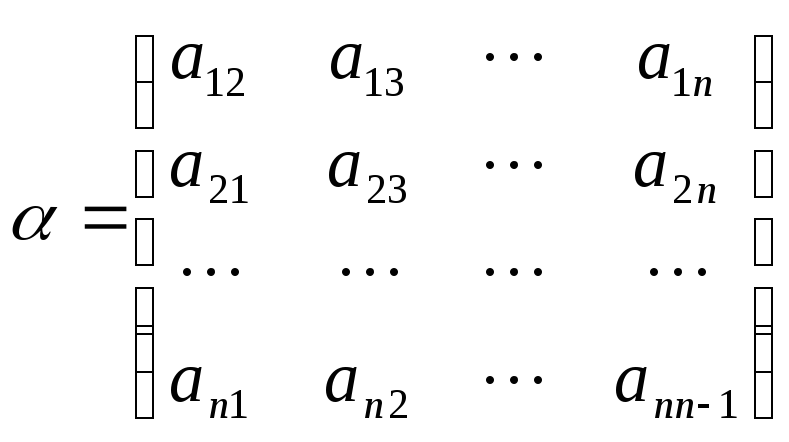и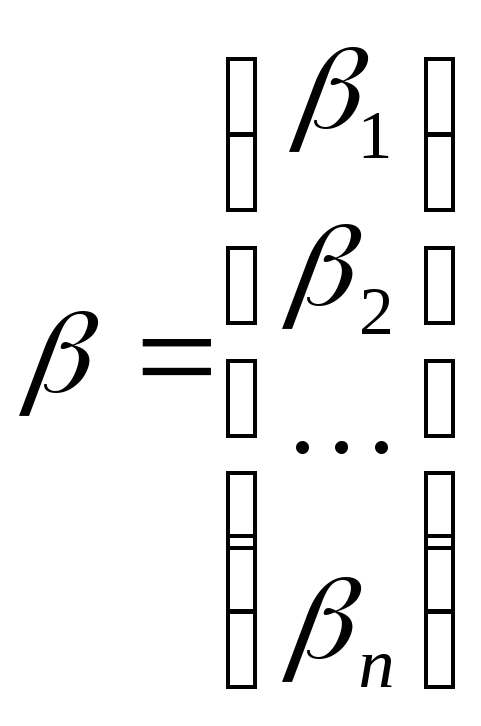

Систему (2) можем записать в матричной форме

(2’)

Систему (2) будем решать методом последовательных приближений. За нулевое приближение принимаем, например столбец свободных членов т.е.

Далее строим матрицы столбцы

Первое приближение

Второе приближение

Вообще говоря, любое (k+1)-е приближение вычисляется по формуле:

(3)

Если последовательность приближений

Имеет предел

То этот придел является решением системы (2). В самом деле, переходя к приделу в равенстве (3) будем иметь:

или

т.е. предельный вектор x является решением системы (2’), а следовательно, и системы (1).

Напишем формулы приближений в развернутом виде

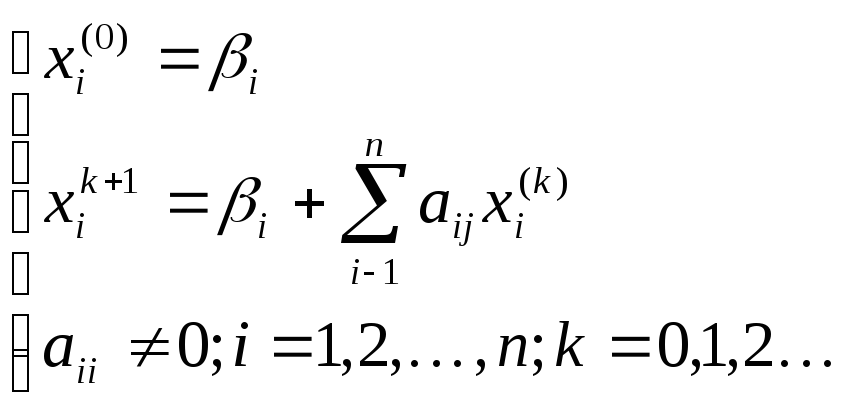
Заметим, что иногда систему (1) выгоднее приводить к виду (2), так чтобы коэффициенты не были равны нулю.

Вообще имея систему:

можно положить

где . Тогда данная система эквивалентна приведенной системе

где

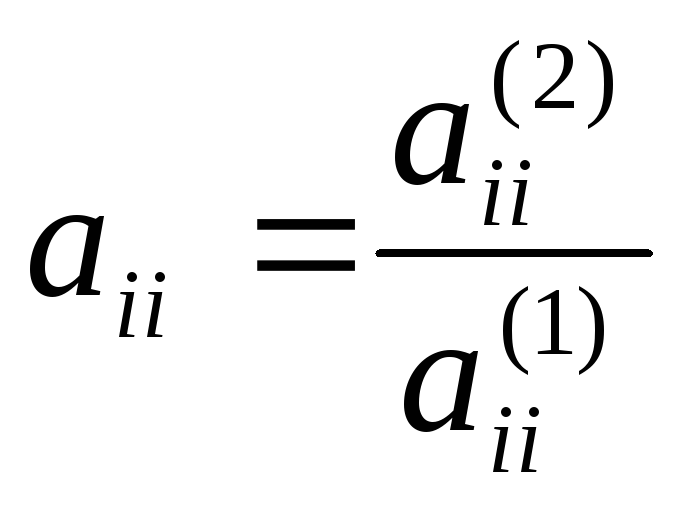
при

Поэтому при дальнейших рассуждениях мы не будем вообще говоря предполагать, что .

Процесс итерации хорошо сходиться т.е. число приближений необходимых для получения корней системы (1) с заданной точностью невелико, если элементы матрицы малы по абсолютной величине. Иными словами, для успешного применения процесса итерации модули диагональных коэффициентов системы (1) должны быть велики по сравнению с модулями недиагональных коэффициентов этой системы (свободные члены при этом роли не играют).

Пример:

Решить систему

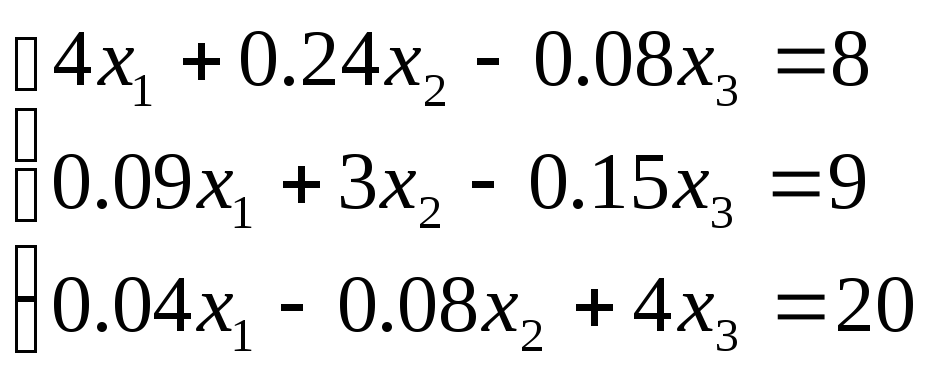
методом итераций

Здесь диагональные элементы, >> чем недиагональные

Приведем эту систему к нормальному вид

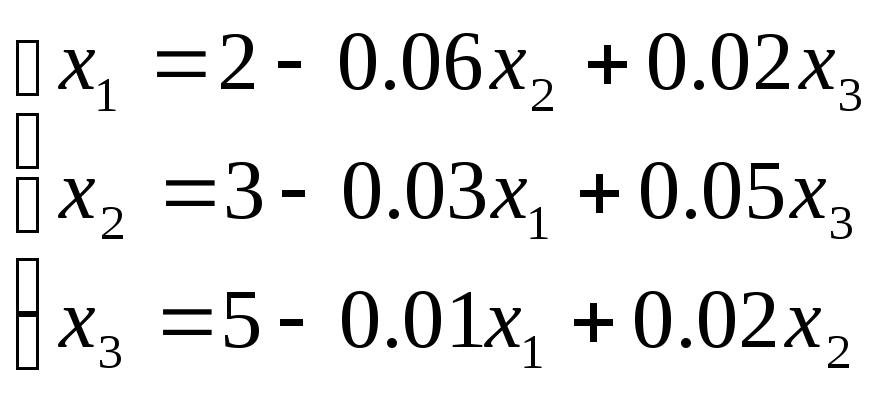
В матричной форме можно записать:

За нулевое приближение принимаем свободное приближение

K
0	2	3	5
1	1.92	3.19	5.04
2	1.9094	3.1944	5.0446
3	1.90923	3.1945	5.04485

Замечание: при применении метода простой итерации нет необходимости брать за нулевое приближение столбец свободных членов. Как будет доказано ниже, сходимость процесса зависит от свойств матрицы .