МатАнализКР-2, 1 вариант

1 вариант

1. Понятие производной. Производная функции х^п.

Пусть функция y=f(x) определена в некоторой точки х₀. Зададим аргументу приращение 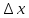такое, что значение находится в указанной окрестности точки х₀. Тогда приращение функции y=f(x) в точке х₀, соответствующее приращению аргумента равно

Производной функции y=f(x) в точке х₀ называется конечный предел (если он существует) при отношения приращения функции в этой точке к соответствующему приращению аргумента.

Производную функции y=f(x) в точке х₀ будем обозначать символом или .

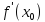По определению производной

Если функция y=f(x) определена на некотором интервале (a,b), то в любой фиксированной точке х этого интервала аналогичным образом определяются приращение и производная в точке х:

Нахождение производной функции называется дифференцированием этой функции.

Если функция в точке имеет конечную производную, то функция называется дифференцируемой в этой точке.

Функция, дифференцируемая в каждой точке промежутка Х, называется дифференцируемой на этом промежутке.

Пользуясь определением производной, получим формулы для вычисления производной :

, где n – натуральное число.

Воспользовавшись формулой бинома Ньютона получим:

10.Производные обратных тригонометрических функций.

Если функция y=f(x) определена, непрерывна и строго монотонна в некоторой окрестности точки х₀ и в этой точке существует производная то и обратная функция имеет производную в точке 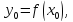причём

С помощью этого можно получить производную функции y=arcsin x, где -1<x<1 и обратную для x=siny.

Аналогично для остальных обратных тригонометрических функций:

Задание №1. Найти производные следующих функций.

Решение:

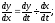
Задание №2. Найти пределы функции, применяя правило Лопиталя.

Решение:

Задание №3. Методами дифференциального исчисления исследовать функцию y = f(x) и по результатам исследования построить ее график. Найти наименьшее и наибольшее значения функции на отрезке [a; b].

Решение:

1. _{Область определения:}

2. _{Функция нечётная:}

3. Пересечение с осями координат: x=0,y=0;

4. Асимптоты функции: y=kx+b – наклонная асимптота, где

Тогда y=0 – наклонная асимптота.

5. Возрастание, убывание функции:

x₁=2; x₂=-2;

- функция убывает

- функция возрастает

y(-2)=-1 – min

y(2)=1 – max

6. Вогнутость, выпуклость функции:

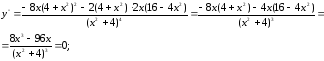
- точки перегиба функции;

- функция выпуклая;

- функция вогнутая;

7. График:

б) I=[-3;3]

Из рисунка видно, что максимум достигается в точке 2, а минимум в точке -2.

Наибольшее и наименьшее значения равны:

y(2)=1 и y(-2)=-1.

Это глобальный максимум и глобальный минимум.

Задание №4. Задана функция y=f(x). Установить, является ли данная функция непрерывной. В случае разрыва функции в некоторой точке найти ее пределы слева и справа, классифицировать характер разрыва. Построить схематично график функции.

Решение:

Точки x₁=-1, x₂=1- подозрительные на разрыв, т.к. меняется аналитическое значение функции.

Для x₁=-1

Значит, функция в т. x₁=-1 – непрерывна.

Для x₂=1

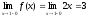
Значит, функция в т. x₂=1 имеет разрыв 1-го рода (функция терпит скачок).

Рисунок: