МатАнализКР-1, 1 вариант

1 вариант

1. Понятие числовой последовательности и ее предела. Теорема об ограниченности сходящейся последовательности.

Пусть множество X — это либо множество вещественных чисел , либо множество комплексных чисел . Тогда последовательность элементов множества X называется числовой последовательностью.

В качестве геометрической интерпретации Ч.П. служит набор точек на числовой оси.

Ч.П. называется ограниченной, если М > 0 такое, что для n имеет место неравенство x_n < М.

Из этого определения возможен вывод : при своем изменении имеется возможность, что x_n приближается к некоторой константе.

Число а называют пределом числовой последовательности {x_n}, если для  > 0 (cколь угодно малое) , для которого всегда найдется такое N, что как только n>N, то будет выполняться неравенство <.

Такую ситуацию символически принято обозначать (записывать) так=а.

Иногда эту ситуацию записывают так: x_nа, при х.

Последовательность, у которой существует предел, называется сходящейся. Последовательность не являющаяся сходящейся называется расходящейся.

Последовательность {x_n} называется сходящейся, если существует такое число а, что последовательность {x_n-а} является бесконечно малой. При этом число а называется пределом последовательности {x_n}.

В соответствии с этим определением всякая бесконечно малая последовательность является сходящейся и имеет своим пределом число ноль.

Можно, также, дать еще одно определение сходящейся последовательности: Последовательность {x_n} называется сходящейся, если существует такое число а, что для любого положительного числа e можно указать номер N такой, что при n³ N все элементы x_n этой последовательности удовлетворяют неравенству:

|x_n-a|<e .

При этом число а называется пределом последовательности.

ТЕОРЕМА: Сходящаяся последовательность ограничена.

Доказательство: Пусть {x_n} - сходящаяся последовательность и а – ее предел. Представим ее в следующем виде:

x_n=а+a _n,

где a _n- элемент бесконечно малой последовательности. Так как бесконечно малая последовательность {a _n} ограничена (по теореме: Бесконечно малая последовательность ограничена.), то найдется такое число А, что для всех номеров n справедливо неравенство |a _n|£ А. Поэтому | x_n | £ |a| + A для всех номеров n, что и означает ограниченность последовательности {x_n}. Теорема доказана.

Ограниченная последовательность может и не быть сходящейся. Например, последовательность 1, -1, 1, -1, … - ограничена , но не является сходящейся. В самом деле, если бы эта последовательность сходилась к некоторому числу а, то каждая из последовательностей {x_n-a} и {x_n+1-a} являлась бы бесконечно малой. Но тогда (по теореме: Разность бесконечно малых последовательностей есть бесконечно малая последовательность.) {(x_n-a) – (x_n+1-a)}={x_n– x_n+1} была бы бесконечно малой, что невозможно т.к. |x_n– x_n+1| = 2 для любого номера n.

10.Теорема об отношении бесконечно малой функции к функции, имеющей предел, отличный от нуля.

Функция y=f(x) называется бесконечно малой при x→a или при x→∞, если или , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.

Примеры.

1. Функция f(x)=(x-1)² является бесконечно малой при x→1, так как (см. рис.).

2. Функция f(x) = tgx – бесконечно малая при x→0.

3. f(x) = ln (1+x)– бесконечно малая при x→0.

4. f(x) = 1/x– бесконечно малая при x→∞.

Отношение бесконечно малой функции α(x) на функцию f(x), предел которой отличен от нуля, есть бесконечно малая функция.

Доказательство. Пусть . Тогда 1/f(x) есть ограниченная функция. Поэтому дробь есть произведение бесконечно малой функции на функцию ограниченную, т.е. функция бесконечно малая.

Задание №1. Найдите пределы функций не пользуясь правилом Лопиталя.

Решение:

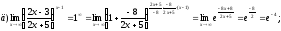
Задание №2. Даны комплексные числа. Необходимо: а) выполнить действия в алгебраической форме; б) найти тригонометрическую форму числа z и вычислить z²⁰ ; найти корни уравнения w³ + z = 0 и отметить их на комплексной плоскости.

Решение:

тогда

Воспользуемся формулой:

для к=0,1…(n-1)

W₂

Задание №3. Исходя из определения равенства множеств и операций над множествами, доказать тождество и проверить его с помощью диаграммы Эйлера – Венна.

Решение:

/x/////////

x ///x//x///////////

/////x // x//////////////

///x///x/////x//////////

/x/xx/x///x///

//x//x//x/////xxx

/x/x/x//xx

xxx -

///// -

x//x -

Из диаграмм Эйлера-Венна видно, что получается одно и тоже множество.

Задание №4.

а) в разложении (x^k + y^P)ⁿ найти члены, содержащие х^ ;

б) в разложении (x + y + z + w)^m найти члены, содержащие х^ .

1. a) k = 2, p = 1, n = 10,  = 4; б) m = 7,  = 5 .

Решение:

a) (x²+y)¹⁰; x⁴ - ?

Воспользуемся формулой Бинома Ньютона:

(x²)¹⁰+C¹₁₀(x²)¹y⁹+C²₁₀(x²)²y⁸+ C³₁₀(x²)³y⁷+…+y¹⁰

C²₁₀x⁴y⁸=(10!/(2!·8!))y⁸x⁴=45y⁸x⁴ , т.е. коэффициент 45y⁸ при x⁴.

б)(x+y+z+w)⁷; x⁵ - ?

(x+y)⁷+C¹₇(x+y)(z+w)⁶+ C²₇(x+y)²(z+w)⁵+ C³₇(x+y)³(z+w)⁴+

+C⁴₇(x+y)⁴(z+w)³+ C⁵₇(x+y)⁵(z+w)²+ C⁶₇(x+y)⁶(z+w)+(x+y)⁷

Рассмотрим все слагаемые, которые содержат x⁵:

1. C⁵₇(x+y)⁵(z+w)²=21(z+w)²(x⁵+C¹₅x⁴y+…+y⁵),

сл-но при x⁵ будет 21(z+w)²;

2. C⁶₇(x+y)⁶(z+w)=7(z+w)( x⁶+C¹₆x⁵y+…+y⁶),

сл-но при x⁵ будет 7 (z+w)6y=42y(z+w);

3. (x+y)⁷= x⁷+ C¹₇x⁶y+ C²₇x⁵y²+…+y⁷,

сл-но при x⁵ будет c;

Тогда в сумме слагаемое содержащее x⁵ выглядит так:

x⁵(21(z+w)²+42y(z+w)+ 21y²)

Задание №5. Задана функция y=f(x). Установить, является ли данная функция непрерывной. В случае разрыва функции в некоторой точке найти ее пределы слева и справа, классифицировать характер разрыва. Построить схематично график функции.

Решение:

Точки x₁=-1, x₂=1- подозрительные на разрыв, т.к. меняется аналитическое значение функции.

Для x₁=-1

Значит, функция в т. x₁=-1 – непрерывна.

Для x₂=1

Значит, функция в т. x₂=1 имеет разрыв 1-го рода (функция терпит скачок).

Рисунок: